МОДА И МЕДИАНА. Модойназывают наиболее часто встречающуюся варианту в вариационном ряду. Класс, в котором находит­ся мода, называют модальным. В вариационном ряду может быть

Модойназывают наиболее часто встречающуюся варианту в вариационном ряду. Класс, в котором находит­ся мода, называют модальным. В вариационном ряду может быть несколько модальных классов.

В примере (распределение суточных удоев у 100 коров) модальным классом является 20,0—21,9 с частотой 24.

Мода может быть вычислена при помощи формулы:

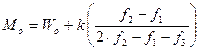
где w_о — нижняя граница модального класса; k — величина классо­вого промежутка; f₁ — частота класса, предшествующего модально­му; f₂— частота модального класса; f₃ — частота класса, следующе­го за модальным.

Подставляя данные из таблицы распределения су­точных удоев коров в формулу, получим:

Как видно, получился показатель, очень близкий к средней арифметической величине 21,26 кг.

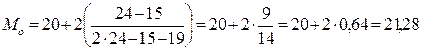
Медианой называют середину класса, который делит вариационный ряд на две части: одна имеет значение признака меньшее, чем медиана, другая — большее.

Приведем пример вычисления М_е вмалых выборках с разным числом дочерей.

Номера кур 1 2 3 4 5 6 7 8 9

Число дочерей (х) 888776554

Номера кур . . 1 2 3 4 5 6 7 8 9 10

Число дочерей (х) .8 8 8 7 5 6_ 5 544

Для первого ряда М_е = 7 гол., для второго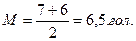

Вычисление медианы в больших выборках при не­равномерном распределении вариантов по классам про­водят по формуле:

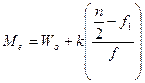
где Wo — начало класса, в котором находится медиана; п — общее число вариант в группе; f\ — сумма частот классов, предшествую­щих классу, где находится медиана; / — частота класса, в котором находится медиана.

Определение медианы проводится путем накопления частот от минимальной величины до величины, не превы­шающей полусуммы всех вариант вариационного ряда. По этой величине устанавливается класс, в котором на­ходится медиана. В данном примере (распределение суточных удоев у 100 коров)

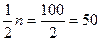
Начало классов . .12 14 16 18 20 22 24 26 28 30

Частоты 3 6 10 15 24 19 14 6 2 1

Накопление частот . . 3 9 19 34 58 (n=100)

Накопление частот: 3+6=9, 9+10=19, 19+15=34. Далее из полусуммы всех вариант совокупности вычи­тается число накопленных частот, меньшее- .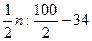

Полученное число умножают на величину к и при­бавляют к величине нижней границы класса, в котором находится М_е:

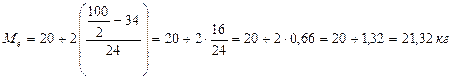
Найденная величина 21,32 также незначительно от­клоняется от средней арифметической 21,26.

Мода и медиана являются вспомогательными вели­чинами, сравнительно редко применяемыми в биологии.

Занятие З.