Краткие теоретические сведения. Всякая группа состоит из особей или объектов, отличающихся друг от друга по каждому из признаков.

Всякая группа состоит из особей или объектов, отличающихся друг от друга по каждому из признаков.

Средняя величина какого-нибудь признака определяется для того, чтобы получить характеристику этого признака для всей изучаемой группы в целом:

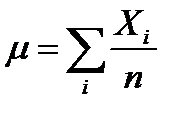. (4.1)

Степень разнообразия особей в группе по изучаемому признаку измеряется несколькими показателями, из которых наибольшее значение имеет стандартное отклонение:

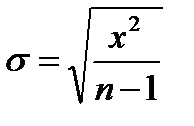. (4.2)

Скошенность кривой называется асимметрией:

. (4.3)

Правосторонняя асимметрия – отрицательна, левосторонняя – положительна.

Отклонение крутизны называют эксцессом:

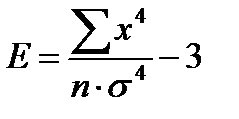. (4.4)

Эксцесс положителен при островершинной кривой, отрицателен при плосковершинной.

Ошибка средней арифметической:

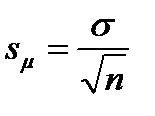. (4.5)

Ошибка стандартного (среднего квадратического) отклонения:

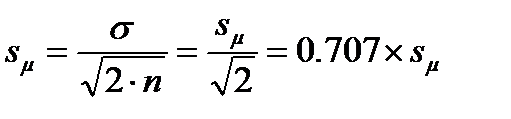. (4.6)

Ошибка показателя асимметрии:

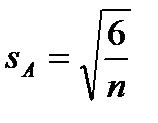. (4.7)

Ошибка показателя эксцесса:

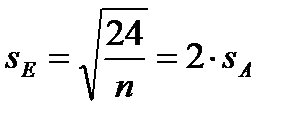. (4.8)

Проверка выбросов (выпадов, артефактов) должна проводиться всегда перед началом обработки полученных первичных данных. Если подтвердится, что резко выделяющееся значение действительно не может относиться к объектам данной группы, и попало в записи вследствие ошибок внимания, следует такой выброс исключить из обработки. Проверка выбросов может производиться по критерию, равному нормированному отклонению выброса:

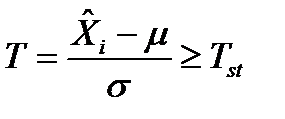, (4.9)

где:

Т – критерий выброса;

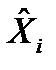– выделяющееся значение признака (или очень большое или очень малое);

μ, s – средняя и сигма, рассчитанные для группы, включающей артефакт;

T_st – стандартные значения критерия выбросов, определяемых по таблице 4.1.

Таблица 4.1 – Стандартные значения критерия выбросов (T_st)

n	Tst	n	Tst	n	Tst	n	Tst
	2,0	16 – 20	2,4	47 – 66	2,8	125 – 174	3,2
3 – 4	2,1	21 – 28	2,5	67 – 84	2,9	175 – 349	3,3
5 – 9	2,2	29 – 34	2,6	85 – 104	3,0	350 – 599	3,4
10 – 15	2,3	35 – 46	2,7	105 – 124	3,1	600 – 1500	3,5

Если Т ≥ T_st, то анализируемое значение признака является выбросом. Альтернатива Т < T_st не позволяет исключить из анализа значение признака.

Для того чтобы оценить генеральный параметр для количественных признаков в форме доверительных границ необходимо:

1 Проверить на нормальность распределения исходных данных.

2 Установить число степеней свободы по правилам, приведенным при описании оценки каждого параметра.

Установить, исходя из ответственности исследования, порог вероятности безошибочных прогнозов (β₁ = 0,95, β₂= 0,99, β₃= 0,999).

В соответствии с числом степеней свободы найти значение критерия надежности t по таблице стандартных значений критерия Стьюдента. При отсутствии таблицы показатель надежности для данного исследования можно приближенно определить по приведенным формулам. Если объем выборки превышает нижние пределы больших выборок (n > 30, n > 100, n > 200), то показатели надежности берутся постоянные для каждого порога вероятности:
t₁ = 2,0; t₂ = 2,6; t₃ = 3,3.

Рассчитать ошибку выборочного показателя.

Определить возможную погрешность оценки генерального параметра, помножив критерий надежности на ошибку репрезентативности: .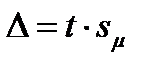

Установить доверительные границы генерального параметра; возможный максимум 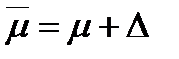и гарантированный минимум .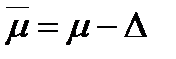