Краткие теоретические сведения. Краткие теоретические сведения изложены в соответствующем разделе лабораторной работы 6.

Краткие теоретические сведения изложены в соответствующем разделе лабораторной работы 6.

Корреляционный и регрессионный анализ

Массив исходных данных приведен в таблице 6.1, который из табличного редактора MS Excel перемещен в таблицу модуля Statistica 6 (рисунок 7.1).

Рисунок 7.1 – Исходные данные
X – независимая переменная
Y – зависимая переменная

Проведем анализ в модуле Basic statistics/Tables(Основная статистика).Рассмотрим и установим связь между X и Y.

Шаг 1. Из Переключателя модулей Statistica откройте модуль Basic statistics/Tables(Основная статистика). Высветите название модуля и далее щелкните мышью по названию модуля: Basic statistics/Tables(рисунок 7.2).

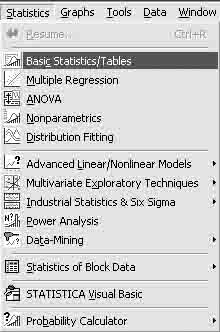
Рисунок 7.2 – Стартовая панель модуля Basic statistics/Tables

Шаг 2. На экране появится (рисунок 7.3). Щелкните мышью по названию Correlation matrics(Корреляционная матрица).

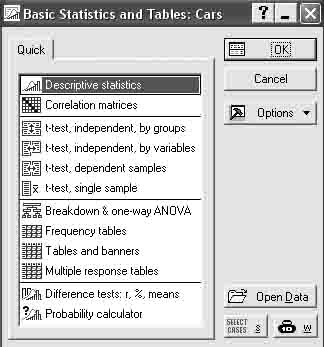
Рисунок 7.3 – Панель запуска

Шаг 3. Выберите переменные для анализа. Выбор переменных осуществляется с помощью кнопки Two list, находящейся в центре верхней части панели (рисунок 7.4).

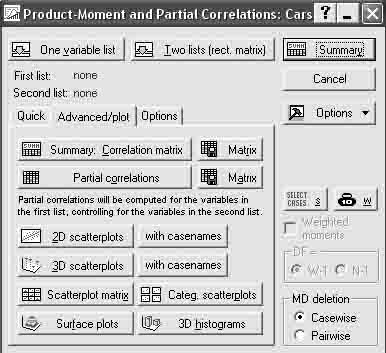
Рисунок 7.4 – Стартовая панель модуляCorrelation matrics

После того как кнопка будет нажата, диалоговое окно Select one or two variable list (выбрать списки зависимых и независимых переменных)появится на вашем экране (рисунок 7.5).

Рисунок 7.5 – Окно выбора переменных для анализа

Шаг 4. Высветив имя переменной в правой части окна, выберите переменную в левой части окна.

После нажатия кнопки OK выполните установки, показанные на рисунке 7.6, подсветив Displey detaled table of results.

Шаг 5. После нажатия кнопки Summary программа произведет
расчет корреляции между X и Y, и на экране появится окно
результатов (рисунок 7.7).

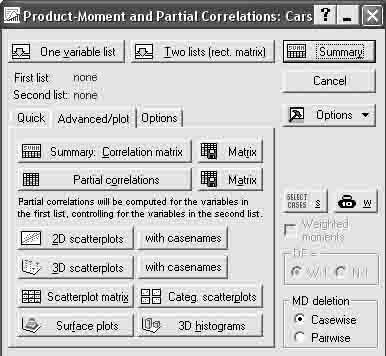
Рисунок 7.6 – Окно предварительных установок

Рисунок 7.7 – Результат расчета корреляции

На рисунке 7.7 представлена следующая информация:

- среднее;

- стандартное отклонение;

- значение коэффициента корреляции r;

- значение коэффициента детерминации r²;

- t – критерий;

- р – уровень значимости;

- число коррелируемых пар;

- 12,67 – свободный член уравнения регрессии.

- 0,82 – коэффициент при независимой переменной уравнения регрессии.

В этом примере r= 0,98. Это очень высокое значение (подсвечено красным цветом), показывающее, что построенная регрессия объясняет более 90% разброса значений переменной X относительно среднего.

Из таблицы видно, что оцененная модель имеет вид:

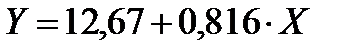
Шаг 6. После нажатия кнопки 2D scatterplots появится график, на котором данные с подогнанной прямой имеют вид (рисунок 7.8).

Рисунок 7.8 – Линейная регрессия для данных X и Y

Задания для выполнения

1 Введите в таблицу Statistica 6 исходные данные из Приложения Б (таблица Б1), предварительно отредактировав и проверив их на наличие артефактов в табличном редакторе MS Excel.

2 Выполните подготовительные и расчетные процедуры в соответствии с порядком операций, выполненных в настоящем разделе.

3 Получите результат и сделайте заключение.

Лабораторная работа 8
Частная и множественная линейные корреляции и регрессия (Statistica 6)

Цель работы: научиться выполнять множественный
корреляционный и регрессионный анализ в программном продукте Statistica 6.