Краткие теоретические сведения. Типичной практической задачей является задача определения зависимостей в системе данных.

Типичной практической задачей является задача определения зависимостей в системе данных.

Предположим, вы наблюдаете значения пары переменных X и Y и хотите найти зависимость между ними.

Переменная X носит название независимой переменной,илипредиктора, переменная Y называется зависимой переменной,или откликом.

Данная терминология связана с тем, что необходимо определить именно зависимость Y от X или предсказать, какими будут значения Y при данных значениях X.

Значение переменной X в i-м опыте будем обозначать через X(i), соответствующее значение величины Y обозначим через Y(i), 0 < i ≤ n.

Вы наблюдаете значения независимой X(i) и соответствующие им значения зависимой Y(i), и хотите оценить зависимость Y от X. В статистике подобные задачи решаются в рамках регрессионной модели. Будем рассматривать самую простую регрессионную модель – линейную. Однако и в рамках этой модели могут быть решены самые разнообразные практические задачи.

Регрессионный анализ в системе Statistica 6 проводится в модуле Multiple regression (Множественная регрессия).

Описание модели

Дадим точное описание линейной регрессионной модели, в рамках которой будем исследовать зависимость Y от Х.

При этом постулируется, что наблюдаемые величины связаны между собой регрессионной зависимостью вида:

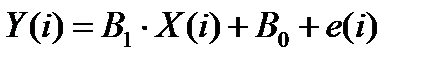, при 0 < i ≤ n

где B₁, В₀ – неизвестные константы, e(i)– ненаблюдаемые
случайные величины (наблюдаются только X(i), Y(i),0 < i ≤ n) со
средним равным нулю (как говорят, являются несмещенными)
и неизвестной дисперсией, не меняющейся от опыта к опыту.

Иногда случайные величины e(i),0 < i ≤ nназывают ошибками наблюдения. Относительно e(i)предполагается, что они не коррелированы в разных опытах. Кроме того, часто предполагается, что ошибки имеют нормальное распределение. В этом случае некоррелированность влечет независимость.

Можно рассматривать и более общие линейные модели, например, с несколькими независимыми переменными:

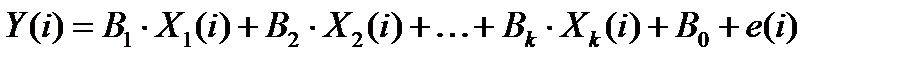, при 0 < i ≤ n,

где B₀, B₁, B₂, ... В_k – неизвестные коэффициенты.

Эта модель также может исследоваться в модуле Multiple regression (Множественная регрессия).

Постановка задачи

Общая задача состоит в том, чтобы по наблюдениям
(X₁, Y₂), ... (X_n, Y_n):

- оценить параметры модели В₁, B₂, В₀ наилучшим образом;

- построить доверительные интервалы для В₁, B₂, В₀;

- проверить гипотезу о значимости регрессии;

- оценить степень адекватности модели.

Ниже на примере выполненных замеров растений определенного вида, где Z – масса растения, Х – высота и Y – диаметр ствола, показано, как решается данная задача в системе Statistica 6.

Введите исходные данные, как показано на рисунке 8.1.

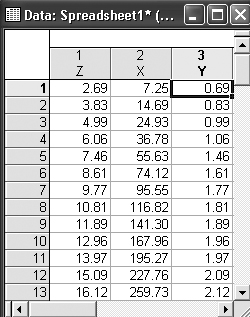
Рисунок 8.1 – Исходные данные
X и Y– независимая переменная; Z– зависимая переменная

Проведем анализ в модуле Multiple regression (Множественная регрессия).

Рассмотрим и установим связь между X, Y и Z.

Шаг 1. Из Переключателя модулей Statistica откройте модуль Multiple regression (Множественная регрессия). Высветите название модуля и далее щелкните мышью по названию модуля Multiple regression (рисунок 8.2).

Рисунок 8.2 – Пусковая панель

Шаг 2. На экране появится стартовая панель модуля (рисунок 8.3).

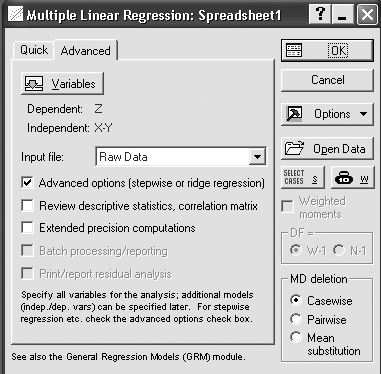
Рисунок 8.3 – Стартовая панель модуля Multiple regression

Выполните установки, как показано на рисунке 8.3. Далее выберите переменные для анализа. Выбор переменных осуществляется с помощью кнопки Variables(Переменные),находящейся в левом верхнем углу панели.

После того как кнопка будет нажата, диалоговое окно Select dependent and independent variable list (Выбрать списки зависимых и независимых переменных) появится на вашем экране (рисунок 8.4).

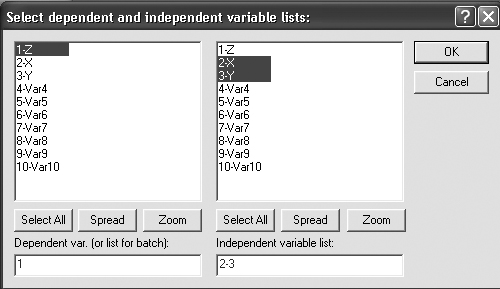
Рисунок 8.4 – Окно выбора переменных для анализа

Высветив имя переменной в левой части окна, выберите зависимые переменные. Высветив имя переменной в правой части окна, выберите независимые переменные.

В данном примере независимыми переменными являются X и Y, зависимой – Z. Высветив имена этих переменных, как показано на рисунке, нажмите кнопку ОК в правом верхнем углу окна Select dependent and independent variable list(Выберите зависимые и независимые переменные). Вы вновь окажетесь в стартовой панели модуля. Переменные для анализа выбраны.

Нажмите кнопку ОК в правом углу стартовой панели.

Шаг 3. На экране перед вами появится диалоговое окно Model Definition(Построение модели) (рисунок 8.5).

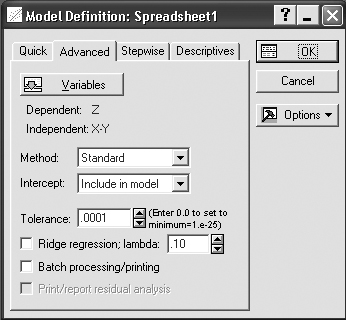
Рисунок 8.5 – Окно построения модели в модуле Multiple Regression

В данном окне выберите стандартный метод оценивания, в опции Method(Метод):Standard(Стандартный).

Далее нажмите кнопку OK.

Программа произведет оценивание параметров модели стандартным методом, и через секунду на экране появится следующее диалоговое окно результатов.

Шаг 4. В диалоговом окнеMultiple Regression Results(Результаты множественной регрессии) просмотрите результаты оценивания. Результаты можно просмотреть в численном и графическом виде.

Окно результатов анализа имеет следующую структуру: верх окна – информационный. Он состоит из двух частей: в первой части содержится основная информация о результатах оценивания, во второй высвечиваются значимые регрессионные коэффициенты. Внизу окна Multiple Regression Results(Результаты множественной регрессии)находятся функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа (рисунок 8.6).

Рассмотрим вначале информационную часть окна.

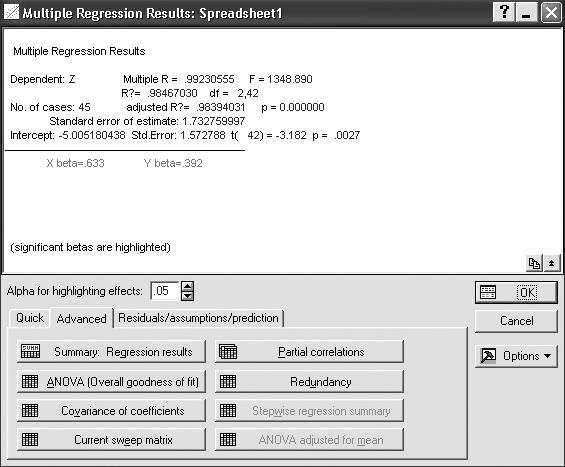
Рисунок 8.6 – Окно оценивания параметров в примере

В ней содержатся краткие сведения о результатах анализа.
А именно:

- Dep. Var. (Имя зависимой переменной). В данном случае: Z;

- No. of Cases (Число случаев, по которым построена регрессия). В примере это число равно 45;

- Multiple R = 0,99 (Коэффициент множественной корреляции);

- R2 (Квадрат коэффициента множественной корреляции), обычно называемый коэффициентом детерминации. Коэффициент
детерминации является чрезвычайно важной характеристикой, поэтому его следует подробно обсудить. Коэффициент детерминации является одной из основных статистик в данном окне, он показывает долю
общего разброса (относительно выборочного среднего зависимой
переменной), которая объясняется построенной регрессией;

- Adjusted R2 (Скорректированный коэффициент детерминации), определяемый как: ,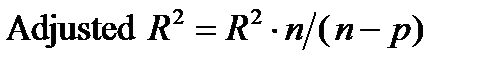

где

- n – число наблюдений в модели, р – число параметров модели (число независимых переменных плюс 1, так как в модель включен свободный член);

- Std. Error of estimate(Стандартная ошибка оценки). Эта статистика является мерой рассеяния наблюдаемых значений относительно регрессионной прямой;

- Intercept(Оценка свободного члена регрессии). Значение коэффициента В₀ в уравнении регрессии;

- Std. Error(Стандартная ошибка оценки свободного члена). Стандартная ошибка коэффициента В₀ в уравнении регрессии;

- t(df) and p-value (Значение t-критерия и уровень р).
t-критерий используется для проверки гипотезы о равенстве нулю свободного члена регрессии.

- F – значения F-критерия;

- df – число степеней свободы F-критерия;

- р – уровень значимости.

В информационной части посмотрим, прежде всего, на значения коэффициента детерминации. Значения коэффициента детерминации лежат в пределах от 0 до 1. В этом примере R² = 0,98. Это очень хорошее значение, показывающее, что построенная регрессия объясняет 98% разброса значений переменной Z относительно среднего.

Далее посмотрите на значение F-критерия и уровень
значимости р. F-критерий используется для проверки гипотезы о значимости регрессии. В данном случае для проверки гипотезы, утверждающей, что между зависимой переменной Z и независимыми переменными X и Y нет линейной зависимости, то есть В₁ = 0иВ₂ = 0, против альтернативы В₁ и В₂ не равны 0. В данном примере наблюдается большое значение F-критерия –1348,89 и даваемый в окне уровень значимости р = 0,0000, показывающие, что построенная регрессия высоко значима.

Перейдем в функциональную часть окна результатов.

Прежде всего, нажмите кнопку Regression summary(Итоговый результат регрессии). На экране появится электронная таблица вывода – spredsheet, в которой представлены итоговые результаты оценивания регрессионной модели (рисунок 8.7).

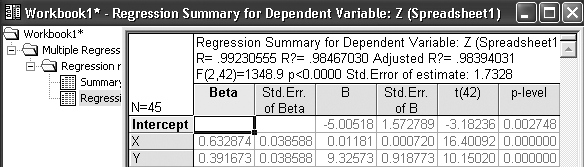
Рисунок 8.7 – Итоговая таблица регрессии

Это стандартная таблица вывода регрессионного анализа. В первом столбце таблицы даны значения коэффициентов beta –стандартизованные коэффициенты регрессионного уравнения, во
втором – стандартные ошибки beta, в третьем – точечные оценки параметров модели.

Свободный член В₀ = – 5,01.

Коэффициент В₁ = 0,012 (при независимой переменной X).

Коэффициент В₂ = 9,33 (при независимой переменной Y).

Далее, стандартные ошибки для В₀, В₁, В₂,значения статистик
t-критерия и т. д.

Из таблицы видно, что оцененная модель имеет вид:

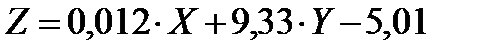
Шаг 5. В окне оценивания параметров (рисунок 8.6) нажмите
кнопку Partial Correlation (Частная корреляция). На рисунке 8.8 высветится результат частных корреляций: r_zx-y = 0,93 (частная корреляция между Z и X при постоянном значении Y) и r_zy-x = 0,84 (частная корреляция между Z и Y при постоянном значении X). Достоверность этих корреляций обусловлена высоким значением
t-критерия и уровнем значимости p = 0,00... Здесь следует обратить внимание на то, что частные коэффициенты корреляции всегда меньше множественного R = 0,99 и соответствующих парных 0,97 и 0,94 (рисунки 8.11 и 8.12).

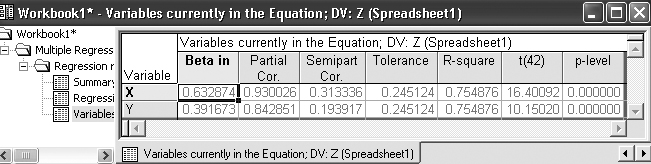
Рисунок 8.8 – Результат расчета частных корреляций

Шаг 6. В окне оценивания параметров (рисунок 8.6) последовательно нажмите кнопки OK(рисунок 8.9), Scatterplot, Bivariate Correlation. В появившемся окне выберите зависимую (Z variable) и независимую
(X variable) переменные (рисунок 8.10 a). Нажмите кнопку OK.

Затем выберите зависимую (Z variable) и независимую
(Y variable) переменные (рисунок 8.10 б). Нажмите кнопку OK.

Рисунок 8.9 – Диалоговое окно Анализ остатков в модуле

На полученных графиках данные с подогнанной прямой имеют вид (рисунки 8.11 и 8.12).

а)

б)

Рисунок 8.10 – Выбор переменных а) – Z и X, б) – Z и Y

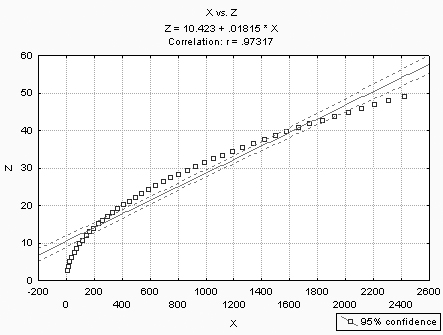
Рисунок 8.11 – Парная корреляция и линейная регрессия между Z и X

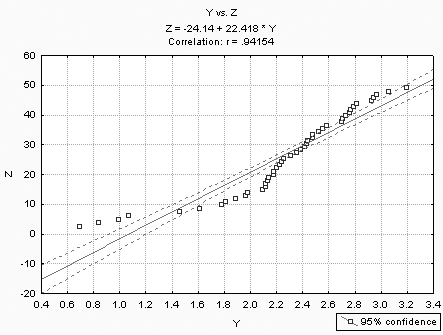
Рисунок 8.12 – Парная корреляция и линейная регрессия между Z и Y

Шаг 7. Оценка адекватности модели.

Важным элементом анализа является оценка адекватности модели. Для этого в окне Диалоговое окно Анализ остатков в модуле (рисунок 8.9) нажмите клавишу Predicted vs. Observed (Модельное и наблюдаемое). Результат обработки представлен на рисунке 8.13. В данном случае адекватность модели наблюдаемым значениям не вызывает сомнений.

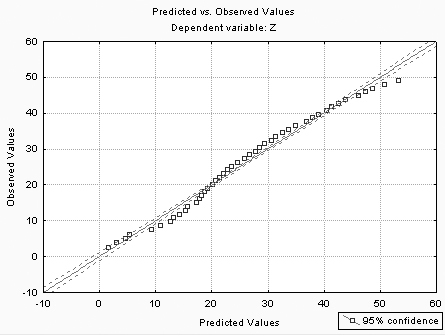
Рисунок 8.13 – Оценка адекватности модели

После того как доказана адекватность модели, полученные результаты можно уверенно использовать для дальнейших действий.

Анализ адекватности основывается на анализе остатков.

Остатки представляют собой разности между наблюдаемыми значениями и модельными, то есть значениями, подсчитанными по модели с оцененными параметрами.

Часто, если остатки не являются нормальными, а также для стабилизации дисперсии применяют преобразования зависимых и независимых переменных, например, логарифмическое преобразование зависимых переменных или извлечение квадратного корня.

Таким образом, применение модуля множественной регрессии показало сильную и достоверную корреляционную связь (R = 0,99;
F(2, 42) = 1348 при р < 0,00..) между массой (зависимая переменная) – высотой и диаметром растений (независимые переменные), которая описывается уравнением линейной регрессии вида:

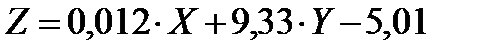
В практическом отношении, следовательно, выполнив ряд замеров высоты и диаметра растений и, зная площадь и густоту посева, можно оценить общую биомассу.

Задания для выполнения

1 Введите в таблицу Statistica 6 исходные данные из Приложения В (таблица В1).

2 Выполните расчетные процедуры в соответствии с порядком операций, выполненных в настоящем разделе.

3 Получите результат и сделайте заключение.

Лабораторная работа 9
Криволинейная корреляция и регрессия
(MS Excel)

Цель работы: научиться выполнять корреляционный и регрессионный анализ в случае предполагаемой криволинейной функциональной связи в табличном редакторе MS Excel.