Суточных удоев 100 коров

Классы (середина) (w)	Частоты (f)	Отклонения (а)	Произведения (fa)
		-4	-12
		-3	-18
		-2	-20	--65
		-1	-15
А-21
		+1	+19
		+2	+28	+78
		+3	+18
		+4	+8
		+5	+5

Эти отклонения обозначаются буквой а. Начинать на­до с класса, середина которого равна 21. Его отклоне­ние от условной средней (А = 21) равно нулю. Класс 19 отклоняется на один классовый промежуток, класс 17—на два, класс 15 — на три, класс 13 — на 4 промежутка. Отклонения этих классов отрицательны, так как их зна­чения меньше, чем условная средняя. Классы 23, 25,27 и т. д. отклоняются от условной средней тоже на 1,2, 3 и т. д. классовых промежутков, но их отклонения положительны, так как их значения больше условной средней. Записав отклонения с их знаками в третью графу таблицы, умножают отклонения каждого класса a на соответствующую частоту f и произведения fa впи­сывают в четвертую графу таблицы. Наконец, суммиру­ют все значения fa с учетом их знака, все положитель­ные (+fa), затем все отрицательные, и вычитают из большей суммы меньшую, сохраняя знак большей ве­личины. В данном примере сумма, положительных значений (+fa) равна +78, сумма отрицательных равна —65. Их алгебраическая сумма ( + 78)+ (—65) = 13.

∑fa представляет собой сумму отклонений вариант от условной средней А, выраженную в числе классовых интервалов. Для вычисления средней арифметической X нужно найти по формуле (4) величину поправки b:

Когда поправка имеет знак «+», ее прибавляют к ус­ловной средней, а когда поправка имеет знак «—», ее отнимают от А.

Прибавив к условной средней - поправку, получают

среднюю арифметическую: Х = A+b = 21+0,26 = 21,26 кг

молока.

Вычисление средней взвешенной (Х_взв).Средняя взвешенная представляет собой результат усреднения средних арифметических нескольких сово­купностей. Она вычисляется по формуле:

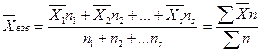(5)

где Хвзв —средняя взвешенная; Х_1,Х₂ Х₃ ...,X_n — средние арифметиче­ские первой, второй и т. д. совокупностей; п, nz,...,n_s — вес (объем) этих совокупностей.

Пример. Известны средняя живая масса и число коров в трех хозяйствах. Они составляли в первом хо­зяйстве Xi = 420, n₁ = 1000, во втором X₂ = 460, n₂ = 500, в третьем Х₃=520, n₃=2000. Нужно вычислить среднюю живую массу коров по данным всех трех хозяйств.

При вычислении средней взвешенной нужно учиты­вать не только среднюю массу коров в каждом хозяй­стве (Х_1, Х₂, X₃), но и объем выборок (п₁, п₂, n₃), по которым были вычислены средние в каждом из хо­зяйств. Средняя -первого хозяйства (Х₁ =420) имеет вдвое больший объем, чем средняя второго хозяйства (Х₂ = 460), Х₁ вычислена по выборке 1000 голов, а Х₂ — по выборке 500 голов. Объем средней третьего хозяй­ства (Х₃=500), вычисленной по выборке 2000 голов, значительно больше объема средней второго хозяйства (Х₂=460), вычисленной по выборке 500 голов. Используя для вычисления средней взвешенной формулу (5), получают:

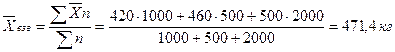
Вычисление средней величины для не­измеряемых признаков (непараметриче­ская средняя). Многие признаки не имеют количе­ственного измерения (интенсивность окраски шкурок цветного каракуля, норок и др.). По степени интенсив­ности развития признака животные могут быть ранжи­рованы в порядке усиления или ослабления выражен­ности признака. Порядковый номер животного называ­ется рангом.

Пример. От двух баранов-производителей (№ 5 и № 6) каракульской породы и группы отобранных маток получено по 8 серых ягнят с различной интенсивностью окраски (от светлой до темно-серой).

Требуется выяснить, какой из производителей дает потомство с более темной мастью. Все потомки обоих баранов-производителей распределены в ранжированный ряд от светло-серой до темно-серой окраски шерсти с указанием номера отца.

Ранги ....1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Номер отца 5 6 5 6 5 5 6 5 5 5 6 5 6 6 6

На основании полученного ряда определяют средний ранг каждого производителя:

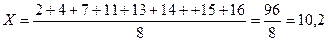
Второй производитель имел больше ягнят с темно-серой окраской, которая ценится дороже.

Понятие о средней геометрической и средней гармо­нической.Для характеристик темпа роста, прироста популяции за определенный период используется сред­няя геометрическая G.

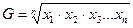(6)

где х - значение варианты; п— число наблюдений в выборке.

Вычисление G проводится путем логарифмирования:

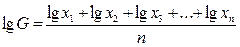
Средняя геометрическая величина используется в асимметрии-чных рядах, когда средняя арифметическая непригодна.

Средняя гармоническая Н используется редко, при усреднении меняющихся скоростей, например при определении средней резвости рысака на разных дистан­циях, пройденных с различной резвостью.