Число подстановок с запрещенными позициями

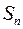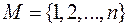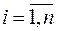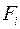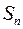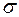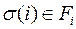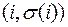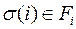Рассмотрим снова группу подстановок множества . Пусть для каждого определено множество запрещенных значений, т.е. из группы исключаются все такие подстановки , для которых . Упорядоченная пара при называется запрещенной парой. Множество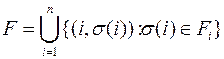

называется запрещенной областью.

На доске, соответствующей матрице подстановок, клетки запрещенной области закрашиваются.

Заметим, что для беспорядков запрещенной областью является главная диагональ.

Чтобы определить число подстановок, которые не принимают значений в запрещенной области, введем для фиксированного 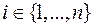множество 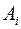как множество всех таких подстановок 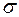, для которых .

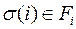Тогда число всех подстановок, значения которых не являются запрещенными, равно

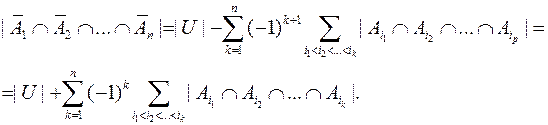
Определим значение 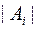при фиксированном 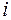. Это будет число всех подстановок, у которых все элементы, кроме 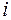-го переставляются как угодно, а 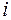-й обязан попасть в одну из закрашенных клеток, т.е. значение подстановки на этом элементе должно принадлежать множеству 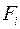. Очевидно, существует 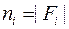способов это сделать. Таким образом, , а .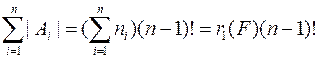

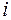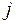Далее, при фиксированных и число 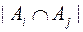равно числу всех перестановок из 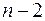элементов, помноженному на число всех способов, которыми можно значения 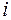-го и 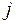-го элементов задать так, чтобы они попали в множества 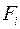и 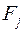соответственно. Это число способов равно, как нетрудно видеть, числу способов, которыми можно разместить две ладьи в той части запрещенной области, которая соответствует множествам 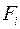и 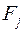. Обозначим это последнее через 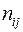. Суммируя 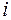по и по 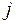, получим

.

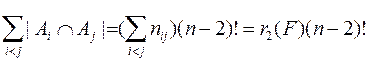Рассуждая аналогично, можно показать, что

.

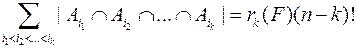Итак, число допустимых подстановок составит

,

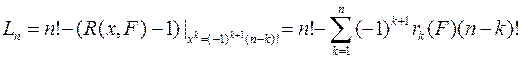т.е. из числа всех подстановок надо вычесть значение ладейного полинома запрещенной области (без единицы) при подстановке вместо 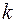-ой степени переменной числа .

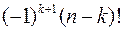Формула может быть, очевидно, переписана и в таком виде:

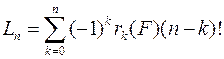
В частности, для беспорядков 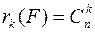- число способов размещения 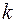ладей на главной диагонали.

Число сюръекций

Формулы включения-исключения можно применить для подсчета числа сюръективных отображений одного конечного множества на другое.

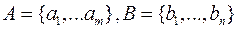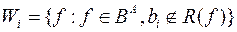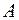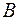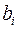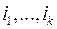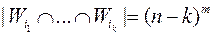Пусть ; пусть - множество всех таких отображений в , в область значений которых не попадает элемент . Тогда для фиксированных имеем , а

.

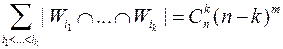Следовательно,

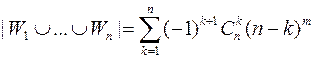
(число всех отображений, не являющихся сюръекциями).

Тогда число 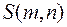всех сюръекций 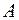на 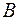составит

.

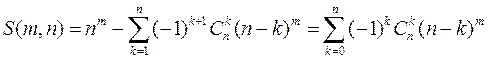Число 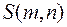может быть получено и по другой формуле:

,

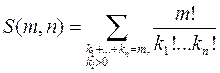где суммирование идет по всем векторам 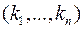с ненулевыми компонентами таким, что сумма компонент равна .

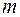Например, 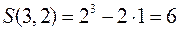по первой формуле, тогда как по второй .

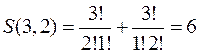Аналогично .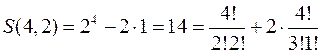

На основании полученных результатов можно вывести формулу для числа всех возможных разбиений 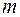-элементного множества на 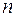подмножеств. Оно будет, как нетрудно показать, равно 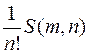[Сачков, с. 44][2]. При этом число разбиений при фиксированных ненулевых числах 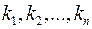будет равно 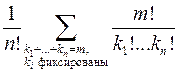, т.е. суммирование ведется по всем различным векторам, компоненты которых суть числа 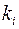. Например, при 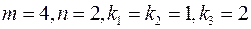получим 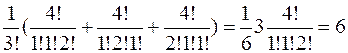, т.е. существует 6 способов разбить 4-элементное множество на 2 одноэлементных и одно двухэлементное. Вот эти разбиения:

1-{1}, {2}, {3,4}, 2-{1}, {3}, {2,4},3-{1}, {4}, {2,3}, 4-{2}, {3}, {1,4}, 5-{2}, {4}, {1,3}, 6-{3}, {4}, {1,2}.

Если в выше написанной формуле для числа сюръекций допустить, что некоторые из чисел 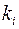могут быть равны нулю, то получим формулу для числа всех отображений m-элементного множества в n-элементное.

По индукции может быть доказана такая формула:

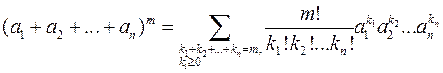
([Сачков, с. 39]).

Тогда при 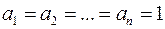получаем 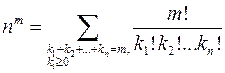, что и равно числу всех отображений m-элементного множества в n-элементное.

[1] Везде в дальнейшем, говоря о размещении ладей, мы, естественно, имеем в виду размещение в неатакующих позициях.

[2] Числа называются числами Стирлинга 2-го рода. [Андерсон, с. 553.]