Структурная идентификация математической модели биологического объекта с использованием методов корреляционного анализа
Лабораторная работа #1
Введение. Одним из первых этапов разработки математической модели нового, т.е. ранее не исследовавшегося объекта является его структурная идентификация, под которой обычно понимают выявление структуры связей между входными, варьируемыми и выходными параметрами, присущими данному объекту. На этом этапе объект обычно представляют в следующем виде (рис. 1.1).
Вектор входных координат (или возмущений) представляет собой набор факторов, которые оказывают воздействие на поведение или состояние этого объекта, но не зависят от желания пользователя. Вектор варьируемых параметров (его часто называют «вектор управлений») представляет собой набор входных параметров, с помощью которых пользователь может оказывать воздействие на объект. И, наконец, вектор выходных координат, представляет собой интересующие свойства объекта (рис. 1.1).
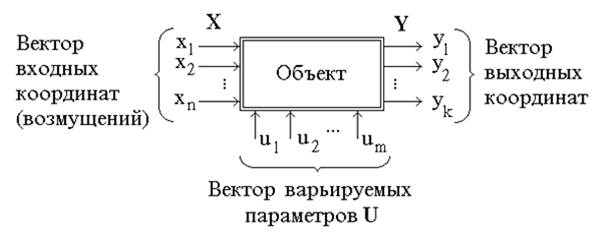
Рис. 1.1. Схематическое представление объекта моделирования.
Математической моделью объекта, представленного на рис. 1.1 является оператор F, связывающий векторы X, U и Y:
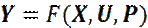 ,
,
здесь P представляет собой вектор параметров этой модели.
На этапе структурной идентификации для объекта, показанного на рис. 1.1 необходимо определить наличие или отсутствие связей по каждому каналу вход – выход и/или оценить «силу» такой связи.
Одним из многочисленных методов структурной идентификации объекта является метод парного корреляционного анализа. На рис. 1.2. показаны различные виды корреляционных полей эмпирических данных, которые могут быть характерны для статических характеристик различных каналов объекта (рис. 1.1).
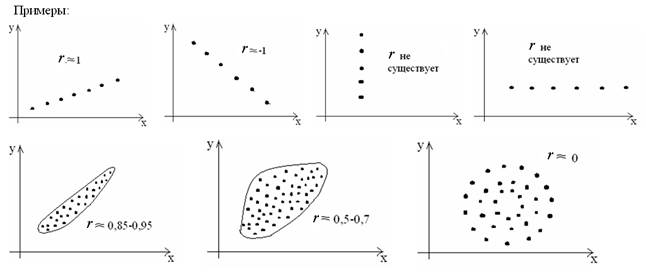
Рис. 1.2. Различные формы корреляционных полей, отражающих статические характеристики объекта, показанного на рис. 1.1.
Расчет коэффициента парной корреляции осуществляется по следующим формулам:
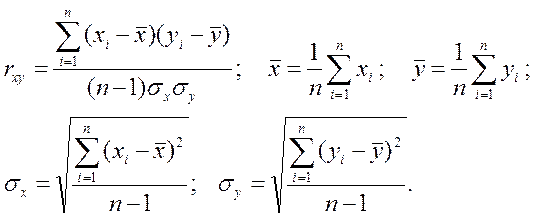
Полученное значение -1£ rxy £1 свидетельствует о «силе» связи. В результате решения задачи структурной идентификации определяют коэффициент парной корреляции по каждому каналу будущей математической модели. Эти результаты оформляют в виде схемы объекта, с нанесенными на каждый канал значениями rxy или в виде таблицы соответствий (пример см. в табл. 1.1).
Таблица 1.1.
Соответствие входов и выходов для объекта, показанного на рис. 1.1.
| Входы объекта | Выходы объекта | |||
| Y1 | Y2 | … | Yk | |
| X1 | 0,2 | -0,4 | 0,98 | |
| X2 | -0,98 | 0,5 | 0,68 | |
| … | ||||
| Xn | -0,01 | 0,4 | 0,3 | |
| U1 | -0,7 | 0,76 | 0,4 | |
| U2 | 0,1 | 0,2 | 0,4 | |
| … | ||||
| Um | 0,9 | -0,8 | 0,76 |
Цели работы:
1) ознакомиться с математическим аппаратом, предназначенным для оценки коэффициентов парной корреляции;
2) разработать программу (можно в MS Excel), позволяющую генерировать псевдоэмпирические данные по различным каналам воображаемого биологического объекта;
3) провести серию вычислительных экспериментов, демонстрирующих различные значения коэффициентов парной корреляции для корреляционных полей различного вида.
Ход работы:
1) с помощью MS Excel сгенерировать таблицу псевдоэмпирических данных, характеризующих одну из статических характеристик биологического объекта;
2) построить график корреляционной зависимости;
3) выполнить расчеты коэффициента парной корреляции по приведенным формулам;
4) провести серию (4-5) вычислительных экспериментов;
5) оформить отчет о проделанной работе в MS Word.
