Критерий достоверности разности
При том большом значении, которое имеет для исследователей получение достоверных разностей, появляется необходимость овладеть методами, позволяющими определить – достоверна ли полученная, реально существующая выборочная разность или, при всей ее материальной действительности, она не достоверна в описанном правильном понимании.
Достоверность выборочной разности измеряется особым показателем, который можно назвать критерием достоверности разности.
Критерий достоверности разности равен отношению выборочной разности к ее ошибке репрезентативности и определяется по формуле:
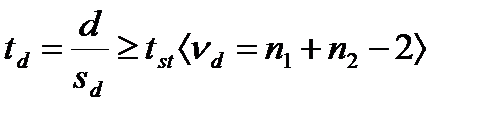 (10.20)
(10.20)
В этой формуле 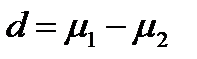 – разность выборочных средних,
– разность выборочных средних,
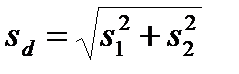 – ошибка выборочной разности, s1, s2 – ошибки репрезентативности сравниваемых выборочных показателей, tst – стандартное значение критерия, определяемое по таблице критериев Стьюдента, для заданного порога вероятности безошибочных прогнозов (0,95, 0,99, 0,999), в зависимости от числа степеней свободы, n1, n2 – численности сравниваемых выборок,
– ошибка выборочной разности, s1, s2 – ошибки репрезентативности сравниваемых выборочных показателей, tst – стандартное значение критерия, определяемое по таблице критериев Стьюдента, для заданного порога вероятности безошибочных прогнозов (0,95, 0,99, 0,999), в зависимости от числа степеней свободы, n1, n2 – численности сравниваемых выборок, 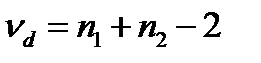 – число степеней свободы для разности двух средних.
– число степеней свободы для разности двух средних.
При использовании критерия достоверности разности возможны два основных случая:
1 td ≥ tst – полученный в исследовании критерий достоверности разности равен или превышает стандартное значение критерия, найденное по Стьюденту. В этом случае разность достоверна с определенной надежностью, т. е. соответствует по знаку генеральной разности.
2 td < tst – полученный в исследовании критерий достоверности разности меньше стандартного значения для минимального или требуемого порога вероятности. В этом случае разность недостоверна, что значит:
- по выборочной разности нельзя сделать никакой оценки генеральной разности;
- осталось невыясненным, какая из двух генеральных средних больше;
- осталось недоказанным как наличие, так и отсутствие различия между генеральными средними.
За минимальный порог достоверности в подавляющем большинстве исследований принимается первый порог, соответствующий вероятности безошибочных прогнозов bi = 0,95.
Техника определения достоверности разности показана на следующих примерах.
Пример
Сравнивался вес взрослых индеек двух пород после одинакового откорма по двум выборкам. Получены следующие сводные показатели:
n1 = 20, μ1±s1 = 4,0 ± 0,3 кг;
n2 = 25, μ2±s2 = 4,6 ± 0,4 кг.
Вторая порода в выборке показала больший вес:
d2-1 = μ2–μ1 = 4,6–4,0 = + 0,6.
Определение достоверности этой разности проведено следующим образом:
d = 0.6; 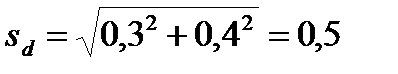
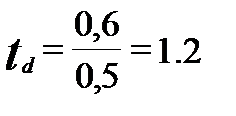 ; n = 20 + 25 – 2 = 43; tst = {2,0 – 2,7 – 3,5}.
; n = 20 + 25 – 2 = 43; tst = {2,0 – 2,7 – 3,5}.
Выводы
- Полученные результаты (d2-1 = + 0,6) свидетельствуют, что в некоторых группах вторая порода может оказаться в среднем тяжелее первой.
- Так как полученная разность оказалась недостоверной, то ничего нельзя заключить о всех представителях обеих пород; осталось невыясненным, какая порода (вся) может иметь больший средний вес; нельзя считать доказанным, что разницы в среднем весе между породами нет и что эти породы в среднем одинаковы по весу.
Пример
Предыдущее исследование было повторено на более обширном материале. Получены новые сводные показатели:
n1 = 100, μ1±s1 = 4,1 ± 0,1 кг;
n2 = 100, μ2±s2 = 4,7 ± 0,1 кг;
d2-1 = μ2 – μ1 = 4,7 – 4,1 = + 0,6 кг.
Определение достоверности разности дало следующие результаты:
d = 0,6; 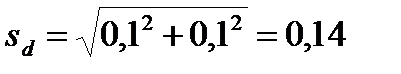
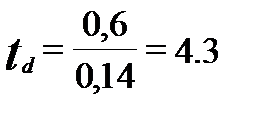 ; n = 100 + 100 – 2 = 198;
; n = 100 + 100 – 2 = 198;
tst= {2,0 – 2,6 – 3,4}.
Выводы
- Полученная разность оказалась достоверна с высшей надежностью (р > 0,999); можно с уверенностью заключить, что вся вторая порода, а не только ее изученная часть, в среднем имеет больший вес взрослых индеек.
- Если нужен прогноз среднего превышения второй породы над первой, например для того, чтобы запланировать экономическим эффект от перемены породы, то это можно сделать обычным методом доверительных границ:
D = tst×sd = 2,0×0,14 = 0,28 » 0,3;
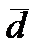 = +0,6±0,3 – [не более +0,6+0,3 = 0,9 кг;
= +0,6±0,3 – [не более +0,6+0,3 = 0,9 кг;
не менее +0,6–0,3 = 0,3 кг;
Гарантированный минимум превосходства второй породы:
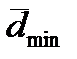 = +0,3 в среднем на голову.
= +0,3 в среднем на голову.
В последнем примере та же по величине разность (0,6), что и в предыдущем, оказалась достоверной вследствие увеличения численности изученных выборок, так как уменьшились ошибки средних.
Так бывает не всегда. Может случиться, что с увеличением численности выборок уменьшается выборочная разность и вследствие этого достоверность ее не повышается; разность остается недостоверной и при большем объеме выборок.
В таких случаях при 2 – 3 повторениях исследования с увеличением численности выборок недостоверная разность уже может считаться доказательством того, что между сравниваемыми генеральными совокупностями не обнаружено различия по изучаемому признаку.
Пример
Изучалось число ядрышек в ядрах соматических клеток серебряного карася у однополых (1) и двуполых (2) особей. Получены следующие сводные показатели:
число исследованных клеток: n1 = 1602, n2 = 1601;
среднее число ядрышек на одну клетку:
μ1 ± s1 = 3.9 ± 0,03; μ2 ± s2 = 2,3 ± 0,02;
разность: d1-2 = 3,9 – 2,3 = +1,6;
Ошибка разности: 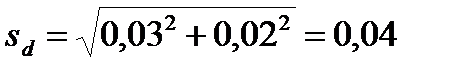 ;
;
Критерий достоверности:
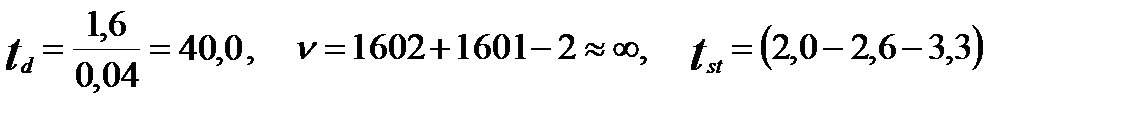 .
.
Разность оказалась в высшей степени достоверной: однополые и двуполые серебряные караси различаются по числу ядрышек на одно ядро в соматических клетках. У однополых число ядрышек в ядрах явно больше.
