Этап 1:Соберем одну грань и поставим центральные кубики на место.
Введение
Кубик Рубика 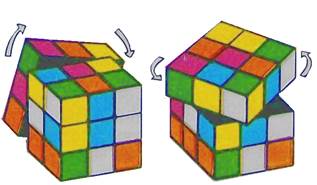 - это пластмассовый куб, разбитый на 27 конгруэнтных кубиков. Внутренний кубик удален, а 26 наружных кубиков с помощью специальных выступов сцеплены так, что любая плитка из 9 кубиков, прилегающих к одной грани куба, может быть повернута в любую сторону на 90°. (Начало двух таких поворотов изображено на рисунке.) После поворота на 90° вся система сохраняет прежнюю свободу вращений: снова любую плитку в любую сторону можно повернуть в ее плоскости на 90°.
- это пластмассовый куб, разбитый на 27 конгруэнтных кубиков. Внутренний кубик удален, а 26 наружных кубиков с помощью специальных выступов сцеплены так, что любая плитка из 9 кубиков, прилегающих к одной грани куба, может быть повернута в любую сторону на 90°. (Начало двух таких поворотов изображено на рисунке.) После поворота на 90° вся система сохраняет прежнюю свободу вращений: снова любую плитку в любую сторону можно повернуть в ее плоскости на 90°.
Первоначально каждая из граней большого куба была окрашена в свой цвет (красный, оранжевый, желтый, зеленый, синий, белый). После ряда случайно выбранных вращений окраска граней куба становится пестрой: на грани присутствуют клетки разных цветов. Головоломка состоит в том, чтобы, получив в руки такой пестрый куб, добиться с помощью вращений правильной расстановки кубиков, то есть такой расстановки, при которой каждая грань куба снова будет одного цвета.
Задача эта совсем не проста. Не вооруженному теорией человеку даже способному, редко удается сразу собрать более одной грани. Число расстановок кубиков, которые можно получить (подсчитано, что их N= 43 252 003 274 489 856 000), делает ее недоступной для перебора даже на ЭВМ. Заметим, впрочем, что не любая расстановка может быть получена вращениями плиток куба: если разрешить разборку куба на составляющие его 26 кубиков, то можно составить 12N = 529 024 039 393 878 272 000 разных расстановок. [1]
Изучив большое количество, литературы я заметила, что почти все варианты сборки кубика Рубика однотипны. Т.е. сначала ставятся на место реберные кубики, а затем угловые. Я же решила найти другой, наиболее оригинальный способ сборки кубика Рубика. Я решила собрать его по слоям, т.е. сначала собрать верхний слой кубика, затем середину и, наконец, низ. Поэтому цель моей работы – разработка оригинального способа сборки кубика Рубика.
Из истории кубика Рубика

В 1974 молодой 30-летний венгр Эрно Рубик, преподаватель Академии прикладных искусств и ремесел после многолетних размышлений создал, то, что в последствии станет называться Кубика Рубика. Много времени ушло на техническое решение, обеспечивающее оптимальный механизм поворота грани куба, результатом которого стал характерный, фирменный скрип. На гранях пробовались и цифры и рисунки, но свой выбор Рубик остановил на цветах.
В 1975 году в социалистической Венгрии Рубик запатентовал свою головоломку.
В конце 1977 года венгерский кооператив выпустил первую партию кубиков. Тогда он назывался "Волшебный Кубик". Случайно немецкий предприниматель с венгерскими корнями - некто Тибор Лакзи увидел Кубика Рубика в руках официанта кафе и занялся ее продвижением на внешний рынок.
1980 год начала реального распространения кубика по всему миру. Американская компания 'Ideal Toy Corporation' дает кубику его правильное имя и заказывает 1 миллион кубиков. Начался бум. За несколько лет было выпущено порядка 100 миллионов кубиков и еще больше подделок. Только «Игра в 15» («пятнашки») изобретенная Sam Loyd, которая в 1870-е годы охватила миллионы людей по обе стороны океана, привлеченных призом в $1000, за решение неразрешимой задачи, могла конкурировать по успеху у землян с Рубиком. Во многих ресторанах кубик стоял на столе как солонка и перечница. Было выпущено около о 60 книг. По разным оценкам каждый 8-10 житель Земли повертел кубику рубика в руках. Кубик получает национальный приз Венгрии как лучшее изобретение, признается лучшей игрушкой в США, Великобритании, Франции и Германии
В 1981 году кубик попадает в экспозицию музея современного искусства в Нью-Йорке (New York Museum of Modern Art). в Англии проходит церемония представления кубика принцу Чарльзу и леди Диане, в честь которых был выпущен специальный тираж. В 1982 кубик Рубика попадает в престижный Оксфордский словарь. Рубик становится первым официальным социалистическим миллионером.
Уже в мае 1980 кубик начал появляться в СССР. Прежде всего, он захватил школы, ученики собирали кубик рубика под партами, а учителя, отобрав его, за классным журналом. Те, кто собирал его быстрее трех минут, пользовались уважением. Официальная цена кубика в СССР была 4,50, как и все, он был дефицитом и из подполы продавался за 10, а то и 20 рублей. В приличной семье старались иметь два кубика, чтобы никто не ждал. Для тех, кто не купил в 1982 году журнал "Юный Техник" печатает статью, как сделать кубик рубика самому. Ряд публикаций по сборке посвятил журнал "Наука и жизнь" 1982 год ознаменовался первым чемпионатом мира по сборке кубика на скорость. Он прошел на родине изобретателя в Будапеште. Рекорд был 22,85 с.
в 1983-1984 В США по субботам шел мультфильм (Rubik, the Amazing Cube), где главный герой - Рубик боролся со злым волшебником. Он умел летать по воздуху и обладал другими паранормальными способностями. Кубик мог жить только, когда его грани были одного цвета.
Но быстрый взлет привел и к быстрому падению, люди накупились кубиков, спрос упал, и рубики стали исчезать с прилавков.
1991 началось постепенное возрождение рубика
1996 в США продано 300 тысяч экземпляров, год спустя в Британии 100 тысяч
В новом веке продажи рубика вновь продолжили свой рост и в 2006 составили 5 млн. штук. На 2007 - 9млн. рубиков! [2]
Терминология
Чтобы изложить предлагаемые правила, условимся сначала о терминологии.
Будем называть центральными кубики, стоящие в центрах граней куба. Каждый центральный кубик всегда (при любых вращениях) остается центральным и смотрит наружу одной клетки определенного цвета.
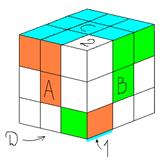
Поскольку нас интересуют не изменения положения всего куба в пространстве, а лишь изменения взаимного расположения его частей, мы будем считать его положение в пространстве фиксированным. Это означает, что положение всех центральных кубиков в пространстве остается неизменным. Это означает так же, что из девяти плоскостей куба мы будем поворачивать только шесть. Если на рисунке некоторая центральная клетка отмечена буквой А, то поворот (не «средней») плитки, содержащей эту клетку, на 90° по часовой стрелке мы будем обозначать через А, а поворот этой же плитки на 90° против часовой стрелки будем обозначать через A-1. Очевидно А-1А-1А-1 =А и А2 = А-2 , где А2 = =А А и А-2= А-1 А-1.
Кубики, содержащие среднюю часть ребра большого куба, будем называть средними. Средний кубик всегда остается средним и смотрит наружу двумя клетками определенного цвета. Для каждой пары цветов (кроме тех пар цветов, которыми первоначально были раскрашены противоположные грани куба) имеется единственный средний кубик с клетками этих цветов.
Угловыми назовем кубики, занимающие в составе куба угловые места. Каждый угловой кубик всегда остается угловым и смотрит наружу тремя клетками, окрашенными в разные цвета. Сочетание этих трех цветов у каждого из угловых кубиков свое. [1]
Невозможные положения
Достаточность предлагаемых ниже «комбинаций» для выполнения перечисленных этапов опирается на три свойства рассматриваемого шарнирного куба.
Если кубики выведены из правильного положения только допустимыми вращениями (а не разборкой и новой сборкой всего устройства или перекраской граней), то не может возникнуть положение, при котором:
I. все средние кубики стоят на своих местах и только один из них повернут неправильно;
II. все средние кубики и стоят, и повернуты правильно, а все угловые кубики, кроме двух, стоят (в любых положениях) на своих местах;
III. все средние кубики и стоят, и повернуты правильно, а все угловые кубики стоят на своих местах и только один из них повернут неправильно.[1]
Основные этапы
Заманчивый, на первый взгляд, путь: постепенно увеличивая пятно одноцветных клеток, получить одноцветную грань, а потом взяться за другую - видимо, приводит лишь к непреодолимым трудностям. Не справившись с головоломкой, ее нередко портят - от злости или из любопытства к устройству шарнира. Я надеюсь, что предлагаемый ниже способ решения сделает головоломку доступной, но и он требует определенных усилий при реализации.
В результате исследования и работы с кубиком Рубика я решила разбить процесс сборки на шесть основных этапов. Как уже говорилось ранее, в ходе решения головоломки центральные кубики не меняют своего положения в пространстве. Что касается средних кубиков, то каждый из них должен в процессе решения занять вполне определенное место: оказаться на ребре между двумя «своими» гранями куба, то есть теми гранями, чьи центральные клетки такого же цвета, как две клетки данного среднего кубика. Кроме того, он должен быть правильно повернут: его цветные клетки должны прилегать к центральным клеткам того же цвета. Совершенно аналогично обстоит дело с угловыми кубиками: у каждого из них есть свое место (на стыке трех граней с центральными клетками его цветов) и единственный правильный разворот.
Каждый из этапов необходимо выполнять только после того, как предыдущий этап полностью закончен. При этом очередной этап выполнять так, чтобы после его завершения оказались не нарушенными достижения предшествующих этапов.
Этап 1:Соберем одну грань и поставим центральные кубики на место.
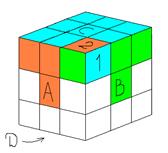
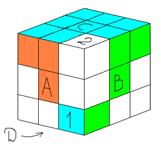
Соберем одну из граней кубика так, чтобы смежные кубики совпали по цвету. И поставим на места центральные кубики (см. рис 1).
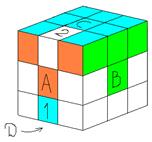
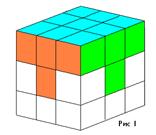
 Для этого обозначим среднюю полосу грани С и А буквой F, а среднюю полосу граней A и B буквой Е. И выполним комбинации при которых 1 2:
Для этого обозначим среднюю полосу грани С и А буквой F, а среднюю полосу граней A и B буквой Е. И выполним комбинации при которых 1 2:
Kа=D-1F-1DF (рис 1а)
Kб=DAD-1A-1 (рис 1б)
Kв=AD-1A-1DAD-1A-1 (рис 1в)
 Kг=(B-1DBD-1)(B-1DB) (рис 1г)
Kг=(B-1DBD-1)(B-1DB) (рис 1г)
|
|
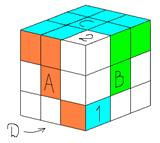 Kд=D-1B-1DB (рис 1д)
Kд=D-1B-1DB (рис 1д) Kе=(F-1DDF)(D-1F-1DF) (рис 1е)
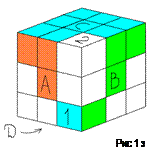
Kж=EAE-1A-1 (рис 1ж)
Kз=E-1B-1EB (рис 1з)
Kи=F-1DDF (рис 1и)
|
|
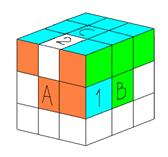
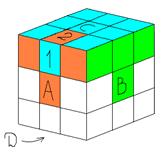
 Kк=(B-1DBD-1)(AD-1A-1) (рис 1к)
Kк=(B-1DBD-1)(AD-1A-1) (рис 1к) 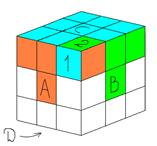
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
 | |||||||||||||
| |||||||||||||
| |||||||||||||
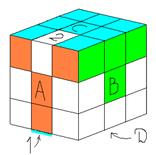
Этап 2:Боковые кубики - на место (рис 4).
 Для этого выполним комбинации, при которой 1 2
Для этого выполним комбинации, при которой 1 2
K1=(D-1B-1DB)(DAD-1A-1)(в том случае если необходимо поставить боковой кубик вправо (см. рис 2))
K2=(DAD-1A-1)(D-1B-1DB)(в том случае если необходимо поставить боковой кубик влево (см. рис3))
