Проверка оптимальности распределения поставок

Транспортная задача

Постановка задачи

Важным частным случаем ЗЛП является транспортная задача. Задача выглядит следующим образом: имеется m поставщиков и n потребителей, мощности поставщиков, спросы потребителей и затраты на перевозку единицы груза для каждой пары «поставщик-потребитель».

Задача представляется в виде таблицы.

Поставщики	Мощность поставщиков	Потребители и их спрос
		…	n
N1	N2	…	Nn
	M1	c11   х11	c12   х12	…	c1n   х1n
	M2	c21   х21	c22   х22	…	c2n   х2n
…	…	…	…	…	…
m	Mm	cm1   хm1	cv2   хv2	…	cmn   хmn

В левом верхнем углу клетки стоит коэффициент затрат c_ij – затраты наперевозку единицы груза от i-го поставщика j-му потребителю.

Задача ставится следующим образом: найти объемы перевозок x_ij для каждой пары «поставщик-потребитель», так чтобы:

1. Мощности всех поставщиков были реализованы.
2. Спросы всех потребителей были удовлетворены.
3. Суммарные затраты на перевозку должны быть минимальны.

Таким образом, для транспортной задачи характерны две системы ограничений:

Первая система ограничений для поставщиков

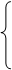х₁₁+х₁₂+…+х_1n=M₁

х₂₁+х₂₂+…+х_2n=M₂

_…

х_m1+х_m2+…+х_mn=M_m

Вторая система ограничений для потребителей

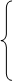х₁₁+х₂₁+…+х_m1=N₁

х₁₂+х₂₂+…+х_m2=N₂

…

х_1n+х_2n+…+х_mn=N_n

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует предположить, что x_ij³0 (i=1,..,m; j=1,…,n).

Суммарные затраты F на перевозку выражаются через коэффициенты затрат и поставки следующим образом: F=c₁₁x₁₁+c₁₂x₁₂+…+c_1nx_1n+…+c_mnx_mn

Математическая постановка задачи

На множестве неотрицательных решений систем ограничени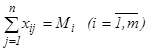й и 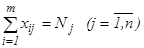найти такое решение Х=(х₁₁,х₁₂,…,х_ij,…,x_mn), при котором линейная функция 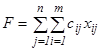принимает минимальное значение.

Транспортные задачи делятся на закрытые (сбалансированные) и открытые.

Закрытая модель-это частный случай транспортной задачи, при которой суммарные мощности поставщиков равны суммарным спросам потребителей.

Открытая модель-это частный случай транспортной задачи, при которой условие равенства суммарных мощностей поставщиков и суммарного спроса потребителей не выполняется.

Нахождение первоначального базисного распределения поставок

По аналогии с другими задачами линейного программирования решение транспортной задачи начинается с построения допустимого базисного распределения. Первоначальное базисное распределение поставок можно найти:

ü методом северо-западного угла;

ü методом минимального элемента;

ü методом Фогеля и т.д.

Проверка оптимальности распределения поставок

Базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.

Правило нахождения оценок свободных клеток: к коэффициентам затрат таблицы поставок в каждой строке и столбце надо прибавить такие числа (потенциалы), чтобы коэффициенты затрат в заполненных клетках стали равными нулю. Полученные при этом коэффициенты затрат свободных клеток равны оценкам этих клеток.