Алгоритм разбора сверху-вниз
Пусть дана КС-грамматика G = (N, T, P, S). Рассмотрим предсказывающий разбор (или разбор сверху-вниз) для грамматики G.
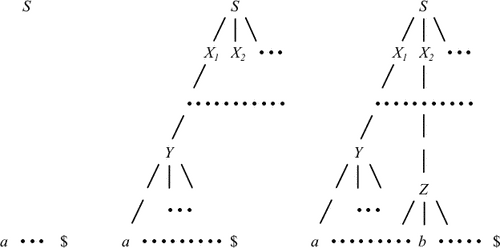
Основная задача предсказывающего разбора - определение правила вывода, которое нужно применить к нетерминалу. Процесс предсказывающего разбора с точки зрения построения дерева разбора проиллюстрирован на рис. 4.1.
|
Фрагменты недостроенного дерева соответствуют сентенциальным формам. Вначале дерево состоит только из одной вершины, соответствующей аксиоме S. В этот момент по первому символу входной цепочки предсказывающий анализатор должен определить правило S  X1X2... , которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y
X1X2... , которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y  a... . Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
a... . Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
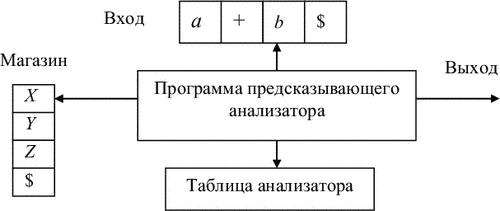
На рис. 4.2 приведена структура предсказывающего анализатора, который определяет очередное правило с помощью таблицы. Такую таблицу можно построить непосредственно по грамматике.
|
Таблично-управляемый предсказывающий анализатор имеет входную ленту, управляющее устройство (программу), таблицу анализа, магазин (стек) и выходную ленту.
Входная лента содержит анализируемую строку, заканчивающуюся символом $ - маркером конца строки. Выходная лента содержит последовательность примененных правил вывода.
Таблица анализа - это двумерный массив M[A, a], где A - нетерминал, и a - терминал или символ $. Значением M[A, a] может быть некоторое правило грамматики или элемент «ошибка».
Магазин может содержать последовательность символов грамматики с $ на дне. В начальный момент магазин содержит только начальный символ грамматики на верхушке и $ на дне.
Анализатор работает следующим образом. Вначале анализатор находится в конфигурации, в которой магазин содержит S$, на входной ленте w$ (w - анализируемая цепочка), выходная лента пуста. На каждом такте анализатор рассматривает X - символ на верхушке магазина и a - текущий входной символ. Эти два символа определяют действия анализатора. Имеются следующие возможности.
1. Если X = a = $, анализатор останавливается, сообщает об успешном окончании разбора и выдает содержимое выходной ленты.
2. Если X = a 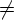 $, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ.
$, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ.
3. Если X - терминал, и X 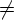 a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
4. Если X - нетерминал, анализатор заглядывает в таблицу M[X, a]. Возможны два случая:
- Значением M[X, a] является правило для X. В этом случае анализатор заменяет X на верхушке магазина на правую часть данного правила, а само правило помещает на выходную ленту. Указатель входа не передвигается.
- Значением M[X, a] является «ошибка». В этом случае анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
Работа анализатора может быть задана следующей программой:
| do {X=верхний символ магазина; if (X - терминал || X=="$") if (X==InSym) {удалить X из магазина; InSym=очередной символ; } else error(); else /*X - нетерминал*/ if (M[X,InSym]=="X->Y1Y2...Yk") {удалить X из магазина; поместить Yk,Yk-1,...Y1 в магазин (Y1 на верхушку); вывести правило X->Y1Y2...Yk; } else error(); /*вход таблицы M пуст*/ } while (X!=$) /*магазин пуст*/ |
Пример 4.3. Рассмотрим грамматику арифметических выражений G = ({E, E', T, T', F}, {id, +, *, (, )}, P, E) с правилами:
E  TE' TE' | T'  *FT' *FT' | ||
E'  +TE' +TE' | T'  e e | ||
E'  e e | F  (E) (E) | ||
T  FT' FT' | F  id id | ||
Таблица предсказывающего анализатора для этой грамматики приведена на рис. 4.3. Пустые клетки таблицы соответствуют элементу «ошибка».

|
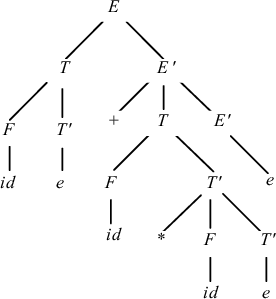
При разборе входной цепочки id + id * id$ анализатор совершает последовательность шагов, изображенную на рис. 4.4. Заметим, что анализатор осуществляет в точности левый вывод. Если за уже просмотренными входными символами поместить символы грамматики в магазине, то можно получить в точности левые сентенциальные формы вывода. Дерево разбора для этой цепочки приведено на рис. 4.5.

| ||
|
Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для 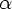 - произвольной цепочки, состоящей из символов грамматики, определим FIRST(
- произвольной цепочки, состоящей из символов грамматики, определим FIRST( 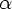 ) как множество терминалов, с которых начинаются строки, выводимые из
) как множество терминалов, с которых начинаются строки, выводимые из 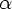 . Если
. Если 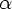
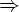 *e, то e также принадлежит FIRST(
*e, то e также принадлежит FIRST( 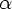 ).
).
Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа от A в некоторой сентенциальной форме грамматики, т.е. множество терминалов a таких, что существует вывод вида S 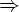 *
* 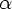 Aa
Aa 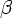 для некоторых
для некоторых 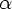 ,
, 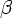
 (N
(N  T)*. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
T)*. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа X  (N
(N  T).
T).
Метод. Выполнить шаги 1-3:
- Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить FIRST(X) =
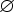 .
. - Если в P имеется правило X
 e, то добавить e к FIRST(X).
e, то добавить e к FIRST(X). - Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
если X - нетерминал и имеется правило вывода X  Y 1Y 2...Y k, то включить a в FIRST(X), если a
Y 1Y 2...Y k, то включить a в FIRST(X), если a  FIRST(Y i) для некоторого i, 1
FIRST(Y i) для некоторого i, 1 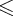 i
i 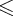 k, и e принадлежит всем FIRST(Y 1), ..., FIRST(Y i-1), то есть Y 1...Y i-1
k, и e принадлежит всем FIRST(Y 1), ..., FIRST(Y i-1), то есть Y 1...Y i-1 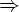 *e. Если e принадлежит FIRST(Y j) для всех j = 1, 2, ..., k, то добавить e к FIRST(X).
*e. Если e принадлежит FIRST(Y j) для всех j = 1, 2, ..., k, то добавить e к FIRST(X).
Алгоритм 4.4. Вычисление FIRST для цепочки.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X1X2...Xn), Xi  (N
(N  T).
T).
Метод. Выполнить шаги 1-3:
- При помощи предыдущего алгоритма вычислить FIRST(X) для каждого X
 (N
(N  T).
T). - Положить FIRST(X1X2...Xn) =
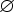 .
. - Добавить к FIRST(X1X2...Xn) все не e-элементы из FIRST(X1). Добавить к нему также все не e-элементы из FIRST(X2), если e
 FIRST(X1), не e-элементы из FIRST(X3), если e принадлежит как FIRST(X1), так и FIRST(X2), и т.д. Наконец, добавить цепочку e к FIRST(X1X2...Xn), если e
FIRST(X1), не e-элементы из FIRST(X3), если e принадлежит как FIRST(X1), так и FIRST(X2), и т.д. Наконец, добавить цепочку e к FIRST(X1X2...Xn), если e  FIRST(Xi) для всех i.
FIRST(Xi) для всех i.
Рассмотрим алгоритм вычисления функции FOLLOW.
Алгоритм 4.5. Вычисление FOLLOW для нетерминалов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FOLLOW(X) для каждого символа X  N.
N.
Метод. Выполнить шаги 1-4:
- Положить FOLLOW(X) =
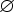 для каждого символа X
для каждого символа X  N.
N. - Добавить $ к FOLLOW(S).
- Если в P eсть правило вывода A

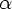 B
B 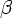 , где
, где 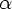 ,
, 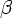
 (N
(N  T)* то все элементы из FIRST(
T)* то все элементы из FIRST( 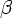 ), за исключением e, добавить к FOLLOW(B).
), за исключением e, добавить к FOLLOW(B). - Пока ничего нельзя будет добавить ни к какому множеству FOLLOW(X), выполнять:
если в P есть правило A 
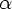 B или A
B или A 
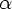 B
B 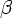 ,
, 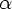 ,
, 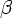
 (N
(N  T)*, где FIRST(
T)*, где FIRST( 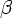 ) содержит e (т.е.
) содержит e (т.е. 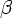
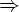 *e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
*e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
Пример 4.4. Рассмотрим грамматику из примера 4.3. Для нее
| FIRST(E) = FIRST(T) = FIRST(F) = {(, id} | |
| FIRST(E') = {+, e} | |
| FIRST(T') = {*, e} | |
| FOLLOW(E) = FOLLOW(E') = { ), $} | |
| FOLLOW(T) = FOLLOW(T') = {+, ), $} | |
| FOLLOW(F) = {+, *, ), $} | |
Например, id и левая скобка добавляются к FIRST(F) на шаге 3 при i = 1, поскольку FIRST(id) = {id} и FIRST(”(”) = {”(”} в соответствии с шагом 1. На шаге 3 при i = 1, в соответствии с правилом вывода T  FT' к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
FT' к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
При вычислении множеств FOLLOW на шаге 2 в FOLLOW(E) включается $. На шаге 3, на основании правила F  (E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E
(E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E  TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку E'
TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку E' 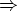 *e, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E
*e, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E  TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
