Ряди номінальних опорів резисторів та ємностей конденсаторів
| Індекс ряду | Номінальні значення (одиниці, десятки, сотні ом, кілоом, мегаом, пікофарад, нанофарад, мікрофарад) | |||||||||||
| E3 | 1,0 | 2,2 | 4,7 | |||||||||
| E6 | 1,0 | 1,5 | 2,2 | 3,3 | 4,7 | 6,8 | ||||||
| E12 | 1,0 | 1,2 | 1,5 | 1,8 | 2,2 | 2,7 | 3,3 | 3,9 | 4,7 | 5,6 | 6,8 | 8,2 |
| E24 | 1,0 1,1 | 1,2 1,3 | 1,5 1,6 | 1,8 2,0 | 2,2 2,4 | 2,7 3,0 | 3,3 3,6 | 3,9 4,3 | 4,7 5,1 | 5,6 6,2 | 6,8 7,5 | 8,2 9,1 |
Примітка. Ряди E представляють собою геометричну прогресію зі знаменником 
, який дорівнює: для ряду E3 
; для ряду E6 
; для ряду E12 
; для ряду E24 
.
6. Обираємо тип операційного підсилювача (ОП). Необхідно, щоб параметри обраного ОП задовольняли наступним вимогам
,
,
де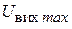 
– максимальна вихідна напруга ОП, 
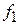– частота одиничного підсилення ОП. Бажано обирати ОП, який має якомога більший коефіцієнт підсилення за напругою та якомога більший вхідний опір. Параметри операційних підсилювачів наведені у довідниковій літературі [7, 8]. Параметри та схеми включення деяких ОП наведені також у Додатках А, Б.
7. Обираємо опір обмежуючого резистора R5
,
де 
– мінімально допустимий опір навантаження для обраного ОП. Згідно з отриманим значенням необхідно обрати найближчий в сторону збільшення стандартний номінал опору (див. табл. 2).
Визначаємо потужність розсіювання
.
8. Визначаємо необхідний коефіцієнт підсилення за напругою
,
де 
– амплітуда напруги на вході підсилювача потужності. При виконанні розрахунків вважаємо, що 
.
9. Обираємо опір резистора R2 в діапазоні від 10 до 50 кОм.
Визначаємо опір резистора R3
.
Приймаємо, що номінальна потужність розсіювання для резисторів R2, R3 дорівнює 0,125 Вт.
10. Визначаємо опір резистора R4
.
Приймаємо, що номінальна потужність розсіювання для резистора R4 дорівнює 0,125 Вт.
11. Обираємо номінальний опір резистора R1 в діапазоні від 500 до 1000 Ом. Визначаємо потужність розсіювання для даного резистора
.
Смуговий фільтр
Електричним фільтром називається частотно-вибірковий пристрій, який пропускає сигнали певних частот і затримує сигнали інших частот. Фільтри нижніх та верхніх частот пропускають відповідно тільки низькі або тільки високі частоти. Смугові фільтри пропускають, а режекторні фільтри, навпаки, не пропускають тільки сигнали певного діапазону (смуги) частот.
Розглянемо передатну функцію фільтру
де 
та 
– напруга на вході та виході фільтру, відповідно.
Зробивши заміну 
( 
), отримаємо комплексний коефіцієнт передачі фільтра
де та 
– амплітуда вхідної та вихідної напруги, 
та 
– фаза вхідної та вихідної напруги. Залежність модуля комплексного коефіцієнту передачі від частоти 
представляє собою амплітудно-частотну характеристику (АЧХ), а залежність аргументу коефіцієнту передачі від частоти 
називається фазочастотною характеристикою (ФЧХ) фільтру.
Смуговий фільтр представляє собою пристрій, який пропускає сигнали в діапазоні частот з шириною смуги 
, яка розташована біля центральної частоти 
, та не пропускає сигнали, частоти яких вище або нижче цієї смуги. На рис. 4 зображені ідеальна та реальна амплітудно-частотні характеристики (АЧХ) смугового фільтру. Частоти 
, 
представляють собою нижню і верхню частоти зрізу фільтра та визначають ширину смуги пропускання 
.
У смузі пропускання амплітудно-частотна характеристика не виходить за межі певного значення (рівень А1 на рис. 4). Існують також дві смуги затримання: 
та 
, де значення АЧХ завжди нижче певного рівня (А2 на рис. 4). Діапазони частот між смугами затримання та смугою пропускання, а саме 
та 
, утворюють відповідно нижню та верхню перехідні області, в яких характеристика є монотонною. Таким чином, реальна АЧХ відрізняється від ідеальної наявністю перехідних областей, а також нерівномірністю характеристики у смузі пропускання та смугах затримання.
Рис. 4. Амплітудно-частотна характеристика смугового фільтру
Відношення 
називається добротністю фільтру та визначає ступінь його частотної вибірковості. Високому значенню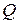 
відповідає відносно вузька, а низькому значенню 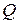– відносно широка смуга пропускання. Коефіцієнт підсилення фільтру 
визначається як значення його амплітудно-частотної характеристики на центральній частоті 
.
Активні фільтри складаються із операційних підсилювачів, які працюють в лінійному режимі, та пасивних RC-елементів. Передатна функція таких фільтрів представляє собою відношення двох поліномів
,
де 
і 
– дійсні коефіцієнти фільтру, 
, 
, 
. Порядок фільтру дорівнює ступені полінома знаменника 
. Чим більший порядок фільтру, тим ближче його АЧХ до ідеальної. Проте підвищення порядку пов’язано з ускладненням схем та більш високою вартістю фільтра.
В залежності від значення коефіцієнтів , розрізняють наступні типи фільтрів: Баттерворта, Чебишева, інверсні Чебишева, еліптичні, Беселя та інші [9, 10].
Фільтр Баттерворта має монотонну амплітудно-частотну характеристику. Такий фільтр називають фільтром з максимально плоскою АЧХ. Характеристика фільтра Чебишева містить пульсації в смузі пропускання (коливання коефіцієнта передачі) і монотонна у смугах затримання. В той же час фільтр Чебишева забезпечує меншу ширину перехідних областей АЧХ, ніж фільтр Баттерворта.
Типову передатну функцію смугового фільтра Баттерворта або Чебишева другого порядку можна записати у наступному вигляді [9]
,
де параметри 
, 
і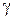 
пов’язані з коефіцієнтами фільтру , .
Для реалізації активних фільтрів Баттерворта і Чебишева найбільш широко застосовуються схема з багатоланковим зворотнім зв’язком (БЗЗ) та схема на базі джерела напруги, що керується напругою (ДНКН).
Схема смугового фільтру другого порядку з БЗЗ зображена на рис. 5, а. Такий фільтр має мінімальне число елементів, інвертуючий коефіцієнт підсилення та може забезпечувати значення добротності 
при невеликих коефіцієнтах підсилення. Для фільтру з БЗЗ мають місце наступні співвідношення
,
,
.
Схема смугового фільтра на базі ДНКН зображена на рис. 5, б. Такий фільтр має неінвертуючий коефіцієнт підсилення та може забезпечувати значення добротності . Опори та ємності елементів фільтру пов’язані з його параметрами наступним чином
,
,
,
де 
, 
.
а
б
Рис. 5. Активні смугові фільтри другого порядку:
а – з багатоланковим зворотнім зв’язком; б – фільтр на базі джерела напруги,
що керується напругою
При виконанні курсової роботи необхідно розробити активний смуговий фільтр четвертого порядку, який складається з двох каскадно включених фільтрів другого порядку. Розглянемо методику розрахунку такого фільтру.
Вихідні дані для розрахунку: тип фільтра (Баттерворта, Чебишева з нерівномірністю АЧХ 0,5 дБ, 1 дБ або 2 дБ); структура фільтра (з багатоланковим зворотнім зв’язком або на базі джерела напруги, що керується напругою); – коефіцієнт підсилення у смузі пропускання; 
– несуча частота АМн сигналу; 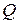– добротність фільтру.