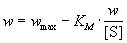Кинетика ферментативного катализа. Уравнение Михаэлиса-Ментен. Уравнение Лайнуивера-Берка
1. Кинетика изучает влияние разных факторов на скорость реакции. Скорость ферментативной реакции (У) измеряют по убыли субстрата или приросту продукта за единицу времени.
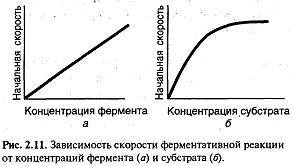
2. Влияние концентрации фермента на скорость реакции: если концентрация субстрата постоянна, то скорость реакции пропорциональна концентрации фермента (рис. 2.11, а).
3. Влияние концентрации субстрата на скорость ферментативной реакции: график зависимости скорости ферментативной реакции от концентрации субстрата имеет вид гиперболы (рис. 2.11, б), как, например, кривая насыщения миоглобина кислородом.
Измеряют скорость реакции почти сразу после начала реакции (начальную скорость) во избежание осложнений зависящих, например, от уменьшения концентрации субстрата, обратимости реакции или образования тормозящих реакцию продуктов.
Интервал времени, в течение которого скорость реакции равна начальной скорости или близка к ней, соответствует прямолинейному участку графика зависимости скорости реакции от времени (рис. 2.12).
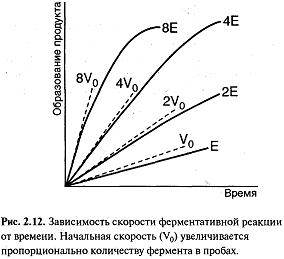
При высокой концентрации субстрата, когда все молекулы фермента находятся в форме фермент-субстратного комплекса, достигается полное насыщение активных центров фермента субстратом, а скорость реакции становится максимальной (VMaKC).
При полунасыщении, когда половина молекул фермента находится в форме ES, скорость реакции равна половине максимальной (1/2 VMaKC). Концентрация субстрата, при которой достигается Vi VMaKC, дает численную величину константы Михаэлиса (4. Константа Михаэлиса Км и максимальная скорость реакции VMaKC — важные характеристики скорости при разных концентрациях субстрата, как указано на рис. 2.13.
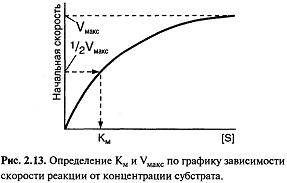
VMaKC — величина, постоянная для каждого фермента, которая позволяет оценить эффективность его действия.
Км показывает сродство фермента к субстрату; чем меньше ее значение, тем больше сродство.
Изоферменты могут различаться по значению Км (для изоферментов глюкокиназы и гексокиназы значение Км различается в 50 раз, и это объясняет их различную физиологическую функцию; см. рис. 2.16).
Если реакция обратима, то взаимодействие фермента с субстратом прямой реакции характеризуется Км, отличающейся от таковой для субстрата обратной реакции (например, карбангидраза для С02 имеет Км, равную 1,2-10-2 М, а для НСО3-KM больше и равна 2,6-10-2 М).
--------------------------------------------------------------------------------------------------------------------------
Простейшая схема ферментативного катализа включает обратимое образование промежуточного комплекса фермента (E) с реагирующим веществом (субстратом, S) и разрушение этого комплекса с образованием продуктов реакции (P):
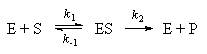
Применение квазиравновесного приближения к этой схеме (при условии k2 << k-1) с учетом уравнения материального баланса [E] = [E]0 - [ES] (индекс "0" обозначает начальную концентрацию) позволяет выразить скорость образования продукта через начальную концентрацию фермента и текущую концентрацию субстрата:
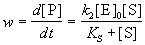
где KS = k-1 / k1 = [E]. [S] / [ES] - субстратная константа. При увеличении концентрации субстрата скорость реакции стремится к предельному значению: wmax = k2. [E]0. Скорость реакции связана с максимальной скоростью соотношением:
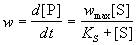 (7.1)
(7.1)
Обычно в эксперименте измеряют зависимость начальной скорости ферментативной реакции от начальной концентрации субстрата: w0 = f([S]0). Проведение таких измерений для ряда начальных концентраций позволяет определить параметры уравнения (7.1) - KS и wmax.
Чаще всего для анализа кинетических схем ферментативного катализа используют метод стационарных концентраций (k2 >> k1). Применение этого метода к простейшей схеме катализа дает уравнение Михаэлиса-Ментен:
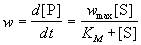 (7.2)
(7.2)
где wmax = k2. [E]0 - максимальная скорость реакции (при бесконечно большой концентрации субстрата),
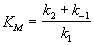
- константа Михаэлиса. Эта константа равна концентрации субстрата, при которой скорость реакции равна половине максимальной скорости. Типичные значения KM - от 10-6 до 10-1 моль/л. Константу скорости k2 иногда называют числом оборотов фермента. Она может изменяться в пределах от 10 до 108 мин-1.
Для практического определения кинетических параметров этот график неудобен, к тому же требует использования концентраций субстрата, «насыщающих» фермент, что не всегда достижимо при ограниченной растворимости субстрата. Поэтому обычно стремятся преобразовать уравнение Михаэлиса-Ментен в такую форму, чтобы графически оно изображалось прямой линией. Чаще всего для этого используют метод Лайнуивера-Берка, представляя уравнение Михаэлиса-Ментен в виде уравнения прямой линии:
Последнее выражение называют уравнением Лайнуивера-Берка и для расчета кинетических параметров используют график, построенный в координатах: 1/V против 1/S. В результате получается прямая, отсекающая на оси ординат отрезок, равный 1/V, а на продолжении оси абсцисс отрезок, равный - 1/Кга. Однако следует отметить, что при использовании графика Лайнуивера-Берка точки в области высоких концентраций субстрата располагаются слишком густо, а положение прямой линии во многом зависит от точек в области низких концентраций субстрата, где определение скорости менее надежно. Кроме того, реальные экспериментальные данные не всегда адекватно аппроксимируются в виде прямой линии: