Производительность и режим работы ВЗУ

Производительность загрузочного устройства определяется заданной производительностью оборудования П₀. На производительность загрузочного устройства оказывает влияние целый ряд эксплутационных и конструктивных факторов, которые практически трудно учесть аналитически. К таким факторам, прежде всего, относятся колебание напряжения в электросети, изменение степени заполнения бункера деталями, количество загруженных деталей и т.п. При прочих равных условиях, производительность также зависит от качества работы привода бункера. Поэтому определяют среднюю расчетную производительность загрузочного устройства П_ср, дет/мин, принимая ее несколько выше производительности П₀.

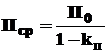, (1)

где k_п - коэффициент нестабильности работы бункерного загрузочного устройства.

Значение коэффициента нестабильности для большинства вибрационных бункеров, согласно экспериментальным данным, может быть принято равнымk_п = 0,2…0,3.

Производительность вибрационных загрузочных устройств связана со скоростью движения деталей по лотку бункера. Для обеспечения требуемой производительности скорость движения деталей V_д, мм/с должна соответствовать:

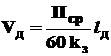, (2)

где l_д - размер детали в направлении движения, мм;

k_з - коэффициент заполнения лотка бункера деталями, движущимися в требуемом ориентированном положении.

Коэффициент заполнения выражается формулой

k_з = 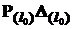, (3)

где P 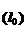- вероятность ориентированного положения деталей на выходном лотке; D 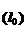- относительная длина детали

.

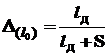Здесь S - среднее значение зазора между движущимися деталями.

Значение вероятности P 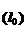зависит от конфигурации детали, физико-механических свойств материала, принятой системы ориентирования конструктивного выполнения ориентиров, установленных на лотках бункера, а также от вероятностей захвата деталей в бункер из навала. Аналитическое определение P 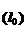для деталей сложной конфигурации затруднительно. Приближенно оно может быть подсчитано для деталей простейшей конфигурации (гладкий валик, втулка, валик с симметричными и асимметричными концами) и призматических деталей с одной и двумя полостями симметрии.

При пассивном ориентировании симметричных валиков и втулок по цилиндрической поверхности для случая l_д > d

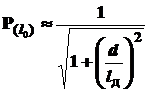, (4)

где d- базовый диаметр детали.

При пассивном ориентировании валиков с асимметричными концами P(l₀)_a определяется по формуле

.

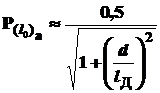При активном ориентировании цилиндрических деталей вероятность движения их в ориентированном положении на выходном лотке может быть определена по формуле (4). Аналогичные формулы для определения P 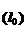могут быть получены для призматических деталей.

При загрузке тонких симметричных пластин (b < l_д >> d) и симметричных длинных цилиндрических деталей (l_д > 10d) можно принять P 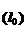» 1.

При загрузке асимметричных деталей, требующих сложных систем ориентирования, вероятность P 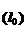удобнее определять экспериментально.

Значение относительной длины D 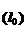в основном зависит от режима работы вибрационного бункера. Если загрузочное устройство работает с подпором, то s= 0, D 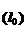= 1. При отрывной подаче деталей D 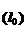определяется экспериментально.

Рассмотрим пример. Пусть требуется определить расчетную среднюю скорость движения детали (d = 7,5 мм, l_д = 19 мм) по лотку вибрационного бункера при активном ориентировании. Деталь подается в рабочие органы сборочного автомата, работающего с производительностью П₀ = 60 дет./мин.

1. Принимая k_п = 0,25, по формуле (1) находим П_ср = 80 дет./мин.

2. По формуле (4) определяем

.

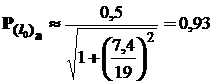3. При работе вибробункера с системой активной ориентации принимаем s = 0; следовательно, D 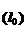= 1.

4. По формуле (3) определяем k_з = 0,93 · 1 = 0,93.

5. Расчетная средняя скорость движения деталей по лотку [см. формулу(2)] составляет

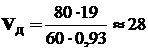мм/с.

Исходя из условия обеспечения средней скорости движения деталей по лотку, определяют основные расчетные зависимости и параметры проектируемых вибрационных питателей.*

Для автоматической загрузки деталей наиболее широкое распространение получили вибрационные бункерные питатели, имеющие гармонический закон колебания лотков бункера. Детали движутся по лоткам при направленных колебаниях лотка под углом α к горизонтальной плоскости. Лотки для транспортировки деталей располагаются на стенках бункера по спирали с углом подъема β.

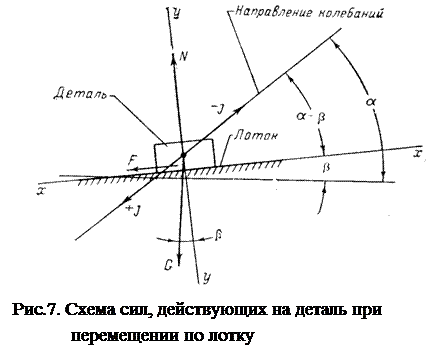
На рис.7 показано направление сил, действующих на деталь, находящуюся на вирирующем лотке. Направим координатную ось xx вдоль лотка под углом β к горизонтальной плоскости, а ось yy- перпендикулярно ей. Рассмотрим в упрощенном виде схему движения детали по лотку, который совершает направленные гармонические колебания с амплитудой A и частотой pпо закону*^*

s = A(1 - cos pt),

где s - текущее перемещение лотка.

На деталь действуют сила тяжести G, сила трения F, возникающая при движении детали по лотку, нормальная реакция N между лотком и деталью, а также сила инерции детали массой m, имеющей ускорениеs¢¢,

j = ms¢¢= mAp²cos pt.

Тогда уравнения относительного движения центра тяжести детали по наклонной поверхности лотка запишутся в следующем виде:

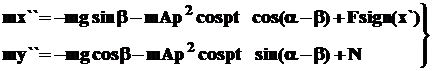, (5)

где x- текущая координата центра тяжести детали;

y- текущая координата нижней поверхности детали.

Сила сухого трения F пропорциональна силе давления между трущимися поверхностями и меняет свое направление при изменении скорости. Для рассматриваемой задачи, когда деталь находится на поверхности лотка, т.е. y = 0, силу трения можно выразить следующим образом:

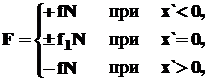
где f и f₁- коэффициенты трения детали по лотку соответственно при движении и покое.

Для анализа явлений, происходящих при перемещении деталей по лотку, воспользуемся вторым уравнением (5), характеризующем действие сил в плоскости, перпендикулярной к основанию лотка. В начальный момент движения (при t= 0 и y= 0) это уравнение примет вид

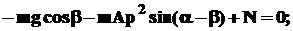
отсюда следует, что в этот момент деталь прижимается к поверхности лотка с наибольшим усилием

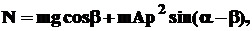
что обуславливает значительную силу трения между деталью и лотком

,

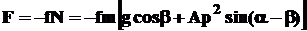направленную в сторону, противоположную направлению движения детали. Увеличению силы трения способствует суммарное действие силы тяжести и силы инерции детали, так что в начальный момент времени, когда скорость движения лотка ещё мала, деталь перемещается совместно с лотком.

В первый полупериод колебания скорость движения лотка и сила инерции детали возрастают по абсолютной величине, при этом уменьшается значение N. Если же значение нормальной составляющей силы инерции превысит нормальную составляющую силы тяжести детали, то деталь начнет отрываться от лотка, т.е. при y >0 N= 0 и F= 0. Таким образом, условие отрыва детали от лотка можно выразить уравнением

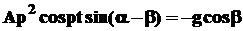. (6)

Обозначим pt = φ - фазовый угол колебательного движения;

φ ₀ - фазовый угол при котором возможен отрыв детали от лотка;

p = 2πn_в- круговая частота вынужденных колебаний;

n_в - частота вынужденных колебаний.

Тогда из выражения (6) получим выражение для фазового угла при граничном условии

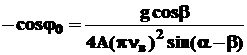. (7)

Значение cosφ ₀ характеризует режим работы вибропитателя. При cosφ₀<1 деталь начнет отрываться от лотка и будет совершать релаксационное движение, Практически удобнее пользоваться обратной cosφ₀ величиной, называемой коэффициентом режима работы вибропитателя:

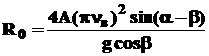. (8)

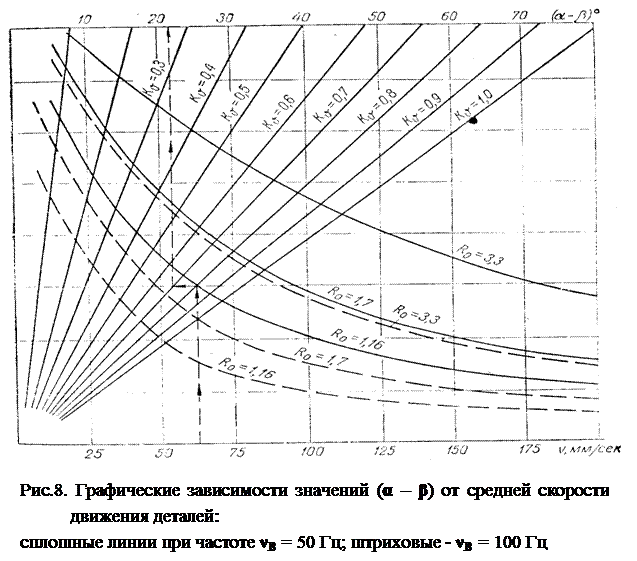
Коэффициент режима работы вибропитателя R₀ определяет скорость движения детали по лотку и максимальный угол подъема лотка (угол спирали). При значениях R₀ =1 движение детали происходит без отрыва от лотка, при
R₀ >1 деталь отрывается от лотка. При R₀ » 3,33 наступает режим непрерывного подбрасывания, соприкосновение детали с лотком происходит в момент удара. Такой режим работы вибропитателя практически непригоден для ориентированной загрузки, так как движение детали неустойчивое и условие ориентации плохое.

В практике проектирования вибропитателей используется режим работы:

1£ R₀ < 3.

При этом режиме определяют все расчетные и конструктивные параметры вибропитателей.

Предельный угол подъема может быть найден по следующим формулам:

1. Для движения деталей по лотку без подбрасывания при R₀ » 1:

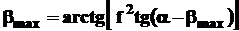. (9)

2. Для движения деталей в режиме с подбрасыванием:

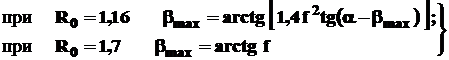(10)

где f - коэффициент трения при движении детали по лотку.

Для расчета средней скорости движения детали по лотку в установившемся режиме работы при угле подъема β, определяемом по формулам (9) и (10), служит выражение

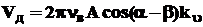, (11)

где k_u- коэффициент, учитывающий снижение скорости по сравнению с максимально возможной:

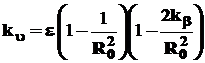(12)

где e = 0,7…0,9; .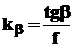

Из уравнений (8) и (11) определим угол бросания

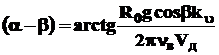, (13)

а следовательно, и угол направления колебания a.

Значение угла a - b можно определить по графикам (рис. 8) в зависимости от требуемой средней скорости движения детали по лотку.

Угол наклона пружинных стержней подвески вибропитателя в вертикальной плоскости связан с углом направления колебания следующей зависимостью:

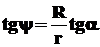, (14)

где R- средний радиус движения деталей по лотку;

r- радиус верхней заделки пружинных стержней.

На режим работы вибропитателя большое влияние оказывает частота вынужденных колебаний, поэтому в практической работе этому вопросу следует уделять особое внимание. При прочих равных условиях, чем больше частота вынужденных колебаний, тем меньше высота подбрасывания детали на лотке, а следовательно, тем лучше условия ориентирования деталей. Для определения режима работы вибробункера необходимо знать высоту подбрасывания детали на лотке (табл. 1).

Таблица 1

Значение высоты подбрасывания детали на лотке вибрационного бункера (в мм)

nв, Гц	R0
	1,6	1,7	3,33
		0,086cosβ 0,019cosβ	0,140cosβ 0,035 cosβ	0,76cosβ 0,19cosβ

Следует, однако, учитывать, что повышение частоты колебаний приводит к необходимости снижения средней скорости движения деталей ввиду возрастания значений ускорений.

Вибропитатели с электромагнитным приводом, включаемые в сеть промышленной частоты, совершают колебания с частотой 100 или 50 Гц.