Расчеты конических зубчатых колес на прочность
Расчеты строят как расчеты эквивалентных цилиндрических колес. Расчетная нагрузка принимается равной силе, отнесенной к средней по ширине венца делительной окружности конических колес:
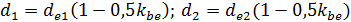
Диаметры эквивалентных цилиндрических колес:
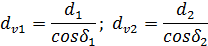
Числа зубьев эквивалентных цилиндрических прямозубых колес:
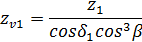 Эквивалентное передаточное число (только для распространения расчетов на контактную прочность цилиндрических передач иа конические):
Эквивалентное передаточное число (только для распространения расчетов на контактную прочность цилиндрических передач иа конические):
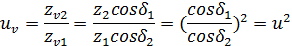
Модуль принимается равным нормальному модулю на середине ширины венца. Для расчета на контактную прочность в формулу для контактных напряжений цилиндрических колес, выраженную через окружную силу 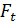 , подставляем:
, подставляем:
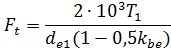
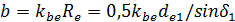 , вместо
, вместо 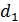 , подставляем
, подставляем 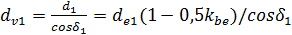 , а u заменяем на
, а u заменяем на 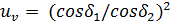 и производим приближенную замену
и производим приближенную замену 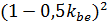 на
на 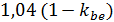 .
.
Кроме того, вводим установленный опытом коэффициент понижения несущей способности конических передач по сравнению с эквивалентными цилиндрическими 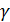 (обычно принимают
(обычно принимают 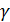 =0,85). После преобразований получаем:
=0,85). После преобразований получаем:
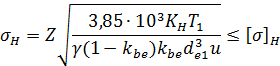
где, как и в цилиндрических передачах 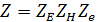 ;
; 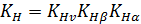 .
.
В отечественной практике большее применение сохранила традиционная форма расчета 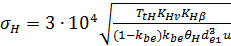
где 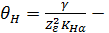 коэффициент, назначаемый для прямозубых передач равным 0,85, а для передач с круговым зубом, определяемый по формулам:
коэффициент, назначаемый для прямозубых передач равным 0,85, а для передач с круговым зубом, определяемый по формулам:
при твердости рабочих поверхностей зубьев шестерни Н1, и колеса Н2 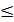 350 НВ:
350 НВ:
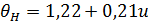
при твердости 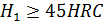 и
и 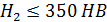
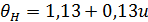
при твердости 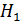 и
и 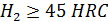
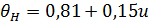
Наружный диаметр шестерни с круговыми зубьями при конструкторском расчете для рекомендуемого отношения 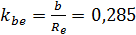 можно найти из формулы:
можно найти из формулы:
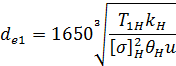
Допускаемое напряжение обычно определяют по менее твердому колесу пары.
Формулы проверочного расчета на изгиб конических зубчатых колес (также с учетом пониженной до 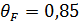 несущей способности по сравнению с цилиндрическими):
несущей способности по сравнению с цилиндрическими):
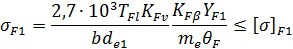
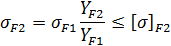
где 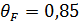 — для прямозубых передач; для передач с круговым зубом определяется в зависимости от твердости шестерни Н1 и колеса Н2 по следующим формулам:
— для прямозубых передач; для передач с круговым зубом определяется в зависимости от твердости шестерни Н1 и колеса Н2 по следующим формулам:
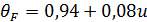 при
при 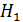 и
и 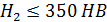
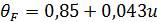 при
при 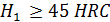 и
и 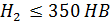
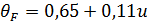 при
при 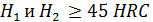
Расчетная формула для проектного расчета конических зубчатых колес, если
основным критерием является прочность на изгиб, а числа зубьев заданы заранее, имеет вид:
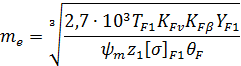
Коэффициент формы зубьев следует выбирать в зависимости от эквивалентных чисел зубьев 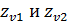 по таблице, увеличенными на 20 %. Круговые зубья с точки зрения прочности отличаются от прямых и косых зубьев дуговой формой и начальным касанием в точке.
по таблице, увеличенными на 20 %. Круговые зубья с точки зрения прочности отличаются от прямых и косых зубьев дуговой формой и начальным касанием в точке.
Червячная передача
Червячная передача (рисунок 3.20) состоит из червяка, т. е. винта с трапецеидальной или близкой к ней резьбой, и червячного колеса, т. е. зубчатого колеса с зубьями особой формы, получаемой в результате взаимного огибания с витками червяка.
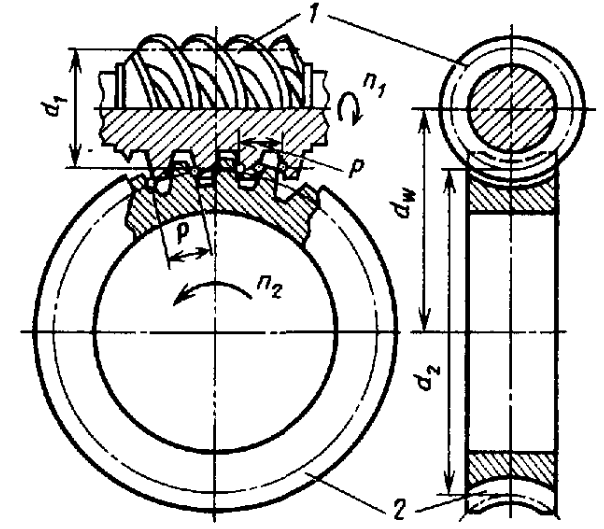
Рисунок 3.20– Кинематическая схема червячной передачи
Червячные передачи относятся к числу зубчато-винтовых, имеющих характерные черты зубчатых и винтовых передач. В отличие от винтовых зубчатых передач с перекрещивающимися осями, у которых начальный контакт происходит в точке, в червячных передачах имеет место линейный контакт.
Зубья червячных колес имеют дуговую форму. Это обеспечивает облегание тела червяка и увеличение длины контактных линий.
Достоинства червячных передач:
а) возможность большого редуцирования;
б)плавность и бесшумность работы.
Недостатки червячных передач:
а) низкий к. п. д.;
б) необходимость применения для колеса дорогих антифрикционных материалов.
Червячные передачи применяют при необходимости редуцирования скорости и передачи движения между перекрещивающимися (в большинстве случаев - взаимно-перпендикулярными) валами. Объем применения червячных передач от передач зацеплением (зубчатых и червячных) составляет около 10%.
Широкое применение червячные передачи имеют в подъемно-транспортных машинах, в станках, автомобилях и других машинах.
Передаточное число и червячной передачи определяют по условию, что за каждый оборот червяка колесо поворачивается на числе зубьев, равное числу заходов червяка:
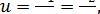
где z1 и z2 - число заходов червяка и число зубьев колеса; n1 и n2 - частоты вращения червяка и колеса, об/мин.
Таким образом, передаточное число определяется отношением числа зубьев колеса к числу заходов червяка и не зависит от соотношения диаметров.
Основные параметры червячных передач.
Червячные передачи вследствие относительно низкого к. п. д. применяют для небольших и средних мощностей от долей киловатта до 200 кВт, как правило, до 50 кВт. Передаточные числа обычно принимают равными от 8 до 100, в специальных случаях, например в приводе столов большого диаметра станков, до 1000. Значения осевых модулей m (мм) выбирают (по ГОСТ 19036-73) из ряда 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5; 16; 20; допускаются m = 1,5; 3; 6; 12. Межосевые расстояния aw по ГОСТ 2144-66: 40; 50; 63; 80; 100; 125; 140; 160; 180; 200; 225; 250; 280; 315; 355; 400; 450; 500 мм.
Геометрия червячных передач
Геометрические расчеты червячных передач аналогичны таким расчетам зубчатых передач. Вначале рассматриваем некорригированное зацепление.
Червяки. В связи с изготовлением червячных колес инструментом, имеющим форму и размеры червяка, сопряженный профиль колеса получается автоматически. Поэтому профиль витков червяка можно варьировать. Выбор профиля в основном определяется технологическими факторами.
Применяют червяки следующих типов: архимедовы, конволютные и близкие к ним - нелинейчатые, эвольвентные, а также с вогнутым профилем.
Архимедовы червяки (рисунок 3.21 а) представляют собой винты с резьбой, имеющей прямолинейные очертания профиля в осевом сечении (трапецеидальный профиль). В торцовом сечении витки очерчены архимедовой спиралью. Эти червяки имеют широкое распространение, как давно известные и наиболее близкие к обычным винтам с трапецеидальной резьбой. Их обычно не шлифуют, так как для шлифования необходима специальная профилировка шлифовального круга.
Под конволютными червяками (рисунок 3.21 б) понимают червяки, имеющие прямолинейные очертания впадины (или витка) в нормальном сечении. В торцовом сечении витки очерчены удлиненной или укороченной эвольвентой. Эти червяки обладают некоторыми технологическими преимуществами перед архимедовыми. При точении резьбы двусторонним резцом (по профилю канавки), а также при нарезании зубьев колеса летучим резцом но обеим боковым граням имеют место одинаковые углы резания.
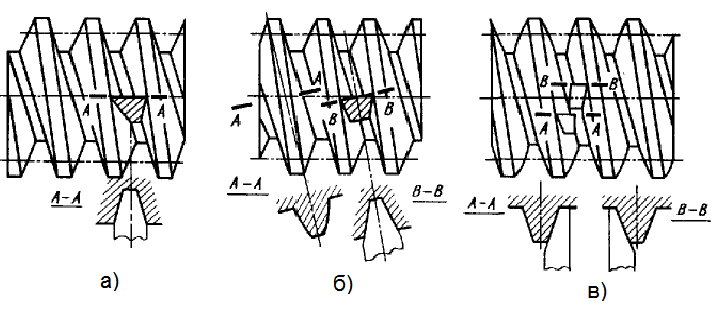
а – архимедов; б – конволюнтный; в – эвольвентный;
Рисунок 3.21 – Основные виды червяков
Червячные колеса(рисунок 3.21). Минимальные числа зубьев колес z2 во вспомогательных кинематических передачах при однозаходных червяках принимают равными 17-18, в силовых передачах z2 = 26 ÷ 28 (если червяк эвольвентный - 17), оптимальными в силовых передачах z2 = 32 ÷ 63 (не более 80). В приводах столов большого диаметра z2 доходит до 200-300, а в отдельных случаях до 1000.
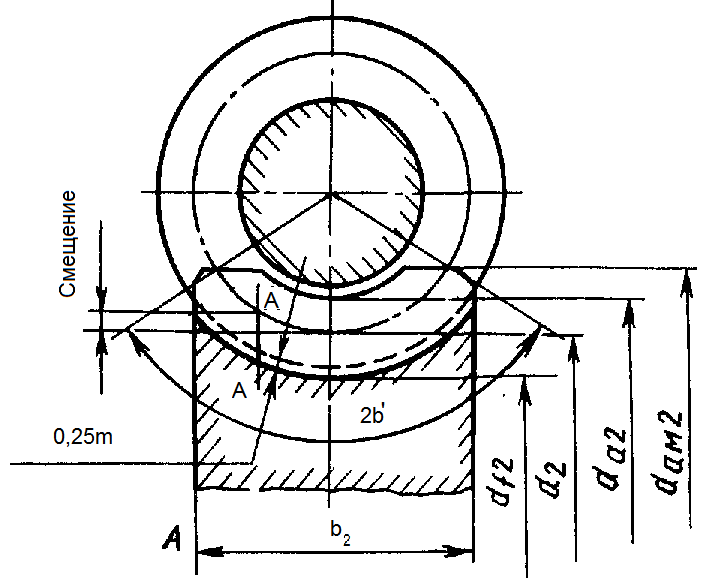
Рисунок 3.22 – Схема червячного колеса
Делительный и совпадающий с ним начальный диаметр 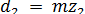 . Ширину колеса выбирают в зависимости от диаметра окружности вершин червяка (рис. 4): при
. Ширину колеса выбирают в зависимости от диаметра окружности вершин червяка (рис. 4): при 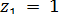 и 2
и 2 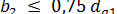 ; при z1 = 4
; при z1 = 4 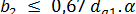
Условный угол обхвата 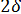 для расчета на прочность находится по точкам пересечения окружности
для расчета на прочность находится по точкам пересечения окружности  m с торцовыми (контурными) линиями червячного колеса, т. е.
m с торцовыми (контурными) линиями червячного колеса, т. е.

Межосевое расстояние передачи равно полусумме диаметров делительных окружностей червяка и колеса, т. е.
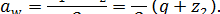
В червячных передачах необходимо предусматривать возможность регулирования при сборке положения червячного колеса вдоль его оси для совмещения с осевой плоскостью червяка.
Расчеты на прочность
Червячные передачи рассчитывают на прочность: по напряжениям изгиба и по контактным напряжениям. В большинстве случаев прочность при изгибе не определяет размеры передачи и этот расчет применяют в качестве проверочного. В качестве проектного расчета на изгиб применяют только при больших числах зубьев колес (более 90 - 100) и для ручных передач. Основное значение имеет расчет по контактным напряжениям, который должен предотвращать в проектируемых передачах выкрашивание и заедание.
Условия зацепления и несущая способность передач с цилиндрическими червяками основных типов весьма близки, особенно при малом числе заходов. Поэтому расчеты, которые ведут в применении к передачам с архимедовым червяком, распространяются на передачи с другими цилиндрическими червяками.
Расчет на изгиб ведут по колесу, так как витки червяков значительно прочнее, и по номинальным напряжениям. Расчет аналогичен расчету косозубых цилиндрических колес только зубья червячных колес принимают на 20-40 % прочнее косозубых. Повышенная прочность зубьев червячных колес связана с их дуговой формой и с так называемой естественной коррекцией, имеющей место во всех сечениях, кроме среднего.
Напряжения изгиба зубьев
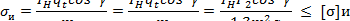
где 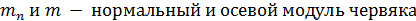 ;
;  - коэффициент прочности зубьев для червячных колес, выбираемый по эквивалентному числу зубьев
- коэффициент прочности зубьев для червячных колес, выбираемый по эквивалентному числу зубьев 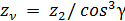 ; [σ]и - допускаемое номинальное напряжение изгиба зубьев колеса, МПа. Множитель cos2γ учитывает наклон контактных линий и работу зуба как пластины.
; [σ]и - допускаемое номинальное напряжение изгиба зубьев колеса, МПа. Множитель cos2γ учитывает наклон контактных линий и работу зуба как пластины.
Расчет по контактным напряжениям ведут по напряжениям в полюсе зацепления, которые не сильно отличаются от максимальных, но определяются проще, чем напряжения в других точках зацепления.
Аналогично расчету зубчатых передач в качестве исходной принимают известную формулу Герца для наибольших контактных напряжений при сжатии цилиндров вдоль образующих 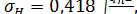 :
:
где Е – приведенный модуль упругости материала; ρν – приведенный радиус кривизны.
Величина 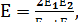
где Е1 – модуль упругости материала червяка; Е2 – модуль упругости материала колеса.
Витки архимедова червяка в средней плоскости имеют профиль прямобочной рейки ρ2 = ∞, а зубья червячного колеса имеют эвольвентный профиль (рисунок 3.23); поэтому расчетный приведенный радиус кривизны равен радиусу кривизны зуба червячного колеса в полюсе зацепления, т. е.
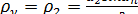 .
.
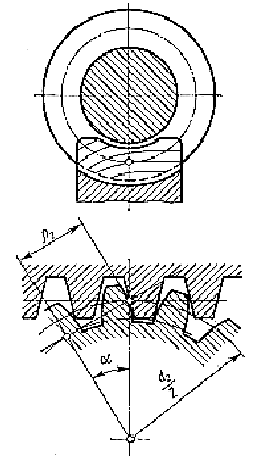
Рисунок 3.23 – Эвольвентный профиль
Подставив в исходную зависимость ρν, а также qn; Р2; d2 = mz2; d1 = mq; 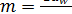 ; α = 200; Е1 = 2,15∙106 кгс/см2; Е2 = 0,9∙106 кгс/см2(для бронзы и чугуна), после преобразований получаем формулу для [σ]Н (МПа)
; α = 200; Е1 = 2,15∙106 кгс/см2; Е2 = 0,9∙106 кгс/см2(для бронзы и чугуна), после преобразований получаем формулу для [σ]Н (МПа)
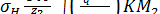 ≤ [σ]Н
≤ [σ]Н
Ременная передача
