Пример решения задания №3

ЗАДАНИЕ №3

Расчет на растяжение–сжатие ступенчатого стержня

Определить напряжения на каждом участке стержня и полную его деформацию. Построить эпюры N, s. Оценить прочность стержня по допускаемым напряжениям. Стержень изготовлен из чугуна: модуль упругости E=1,2*10⁵ МПа, предел прочности на растяжение 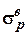=113 МПа, предел прочности на сжатие 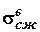=490 Мпа (рис.3.1, табл.3.1).

Требуется выполнить следущее

1. Вычертить схему стержня со всеми числовыми данными.

2. Определить внутренние усилия на каждом участке.

3. Определить напряжения на каждом участке.

4. Оценить прочность каждого участка стержня по допускаемым напряжениям,

5. Определить деформацию каждого участка и полную деформацию стержня.

6. Вычертить схему с эпюрами продольных сил N, напряжений s.

Таблица 3.1

Вариант	Продольная сила, кН	Площадь поперечного сечения А, м2	Длины участков
F1	F2	F3	l1, м	l2, м	l3, м
				3,0×10-3	0,2	0,4	0,2
				3,2×10-3	0,4	0,2	0,2
				2,8×10-3	0,4	0,5	0,2
				2,7×10-3	0,2	0,2	0,3
				2,4×10-3	0,2	0,3	0,4
				2,6×10-3	0,5	0,2	0,2
				2,0×10-3	0,3	0,3	0,4
				1,6×10-3	0,5	0,2	0,3
				1,8×10-3	0,2	0,5	0,2
				2,5×10-3	0,5	0,2	0,4

При сжимающей силе в опасном сечении расчет проводят по допускаемым напряжениям на сжатие: 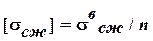, а при растягивающей продольной силе – по допускаемым напряжениям на растяжение: 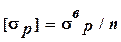, где n – коэффициент запаса прочности (в задаче принять n=1,5), 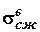, 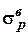– пределы прочности материала соответственно на сжатие и растяжение.

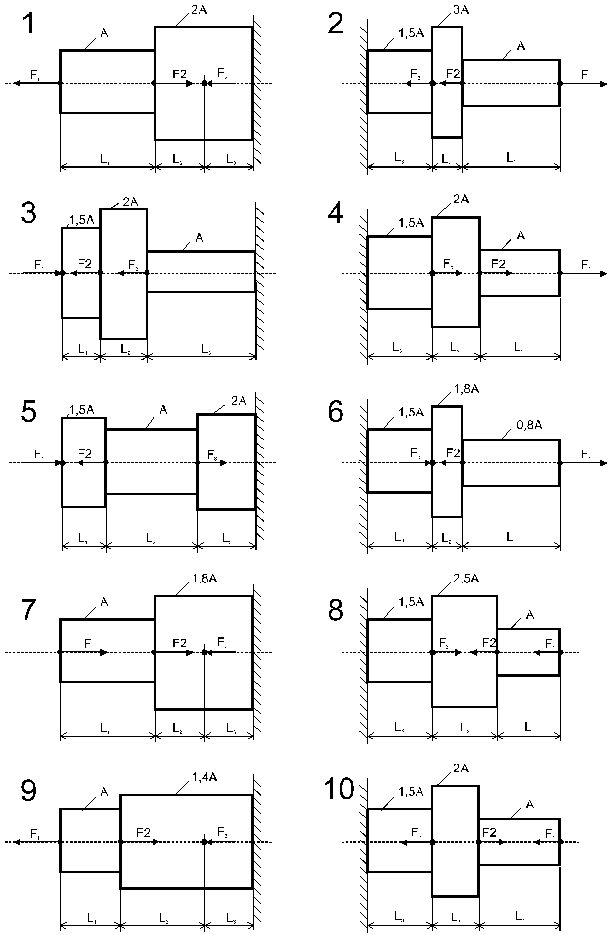
Рис.3.1

Указания к заданию №3

Эпюры продольных сил необходимо строить, руководствуясь правилом: продольная сила в любом сечении стержня равна алгебраической сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на ось стержня. Продольная сила считается положительной, если она соответствует деформации растяжения.

При сжимающей силе в опасном сечении расчет проводят по допускаемым напряжениям на сжатие: 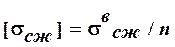, а при растягивающей продольной силе – по допускаемым напряжениям на растяжение: 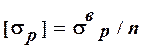, где n – коэффициент запаса прочности (в задаче принять n=1,5), 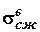, 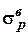– пределы прочности материала соответственно на сжатие и растяжение.

Пример решения задания №3

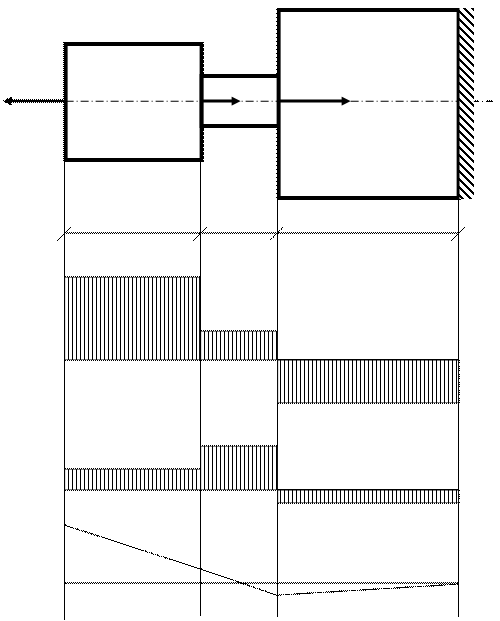
Задание. Для заданного ступенчатого стержня (рис.3.2), изготовленного из чугуна построить эпюры продольных сил и нормальных напряжений по длине; проверить брус на прочность.

Дано: L₁=0,3м; : L₂=0,2м; : L₃=0,4м; А=10^-3м²; А₁=2*А=2*10^-3м²; А₂=0,5*А=0,5*10^-3м²; А₃=3*А=3*10^-3м²;

F₁=40кН;. F₂=20кН;. F₃=50кН;.

Допускаемое напряжение для материала стержня 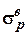=113МПа, 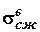=490МПа. Модуль упругости E=1,2*10⁵ МПа, коэффициент запаса прочностиn=2.

Решение. Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил или местами изменения размеров поперечного сечения. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая правые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке.

3A

2A

A

F₁ F₃

F₂

L₁ L₂ L₃

I участок II участок III участок

N, kH

-30

-10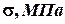

8,33*10^-5

3.33*10^-5

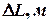
-3.33*10^-5

Рис.3.2

Для того, чтобы определить усилие N_I, проводим сечения в пределах первого участка. Рассмотрим равновесие оставшейся левой части стержня (рис.3.3).

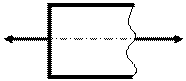F₁ N_I

Рис.3.3

Из уравнения равновесия оставшейся левой части выразим внутреннюю продольную силу N_I через внешние силы, приложенные к оставленной части

N_I = F₁ = 40= 40 кН

Так как положительное направление совпадает с деформацией растяжения, то знак плюс означает, что на первом участке осуществляется деформация растяжения.

Аналогично находим внутреннее усилие N_II, действующее на втором участке. Для этого проводим произвольное сечение на втором участке и рассматриваем равновесие оставшейся левой части стержня (рис.3.4).

F₂

F₁ N_II

Рис.3.4

Уравнение равновесия в проекции на ось стержня для второго участка

F₁ – F₂ – N_II = 0

Решая это уравнение, получим

N_II = F₁ – F₂ = 40–20 = 20 кН.

Знак плюс означает, что на втором участке осуществляется деформация растяжения.

Для того, чтобы определить внутреннее усилие N_III, действующее на третьем участке рассмотрим равновесие оставшейся части стержня (рис.3.5)

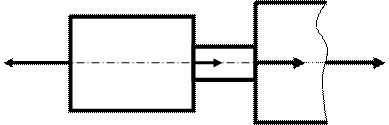
F₁ F₂ F₃ N_III

Рис.3.5

Уравнение равновесие в проекции на ось стержня для схемы, представленной на рис.3.5

F₁ – F₂ – F₃ – N_III = 0.

Решая это уравнение, получим

N_III = F₁ – F₂ – F₃ = 40–20 – 50= -30 кН.

Таким образом, в заделке действует реакция равная N_III =-30 кН.

Знак минус означает, что на третьем участке осуществляется деформация сжатия.

Эпюра продольных сил показана на рис.3.2.

Чтобы определить напряжение в поперечных сечениях бруса, нужно разделить числовые значения продольных сил на площади этих сечений.

Для первого участка

.

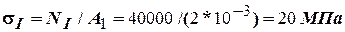Допускаемые напряжения при растяжении, при условии, что коэффициент запаса n=2

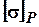=113/2=56,5 Мпа.

Условие прочности для первого участка выполняется

.

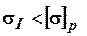Недогруз конструкции на первом участке составил =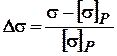

= (20-56,5) / 56,5*100% = –64,6%, что выше допустимого (10%).

Для второго участка

.

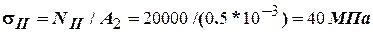Условие прочности для второго участка выполняется

.

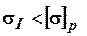Недогруз конструкции на втором участке составил

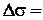(40–56,5) / 56,5*100%=29,2%, что выше допустимого (10%).

Для третьего участка

.

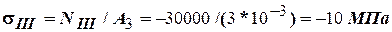Допускаемые напряжения при сжатии, при условии, что коэффициент запаса n=2

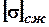=490 / 2=245 МПа.

Условие прочности для первого участка выполняется с большим запасом

.

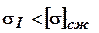Недогруз конструкции на третьем участке составил

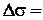(10-245) / 245*100% = – 95,9%.

Эпюра нормальных напряжений по длине бруса показана на рис. 3.2.

Удлинения (укорочения) участков бруса определяются по формуле

,

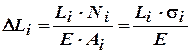где 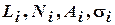– соответственно длина участка, внутреннее усилие, площадь поперечного сечения, напряжение в сечении. Е–модуль упругости материала.

Удлинение первого участка

.

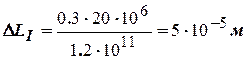Удлинение второго участка

.

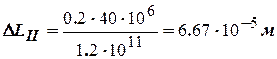Укорочение третьего участка

.

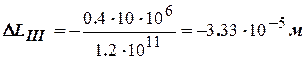В правом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры смещения стержня необходимо строить, начиная с правого конца (рис.3.3).

На третьем участке смещение изменяется от 0 до 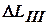=-3,33*10^-5м;

на втором от 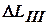=-3,33*10^-5м до 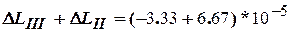=3,33*10^-5м;

на первом от 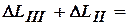3,33*10^-5м до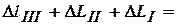

+(-3,33+6,67+5)*10^-5=8,33*10^-5м.

Полное удлинение бруса составило 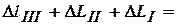8,33*10^-5м.