Расчет и конструирование спирального сверла

Задание:

Рассчитать и сконструировать спиральное сверло из быстрорежущей стали для сверления под последующую технологическую операцию. Диаметр сверла выбрать исходя из технологического назначения отверстия.

Обрабатываемый материал: Чугун СЧ35.

Предел прочности: σ_в =180 МПа.

Глубина сквозного отверстия: l = 10 мм.

Назначение сверления: на проход под заклепку d = 19 мм.

Решение:

Материал рабочей части сверла принимаем быстрорежущую сталь Р6М5 (табл. 1, [1], стр. 34), материал хвостовика принимаем сталь 45.

2.1 Определение наружного диаметра D.

Для сверления на проход под заклепку d = 19 мм принимаем диаметр сверла равным D = 19 мм ГОСТ 10903-77 (табл. 41, [2], стр. 145).

2.2 Определяем режим резания. При сверлении чугуна с пределом прочности σ_в = 180 МПа подачу на оборот принимаем равной: S_о = 0,41 мм/об (табл. 25, [2], стр. 276).

Скорость главного движения резания, допускаемая режущими свойствами сверла:

(1) 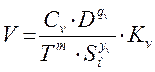, ([2], стр. 276)

С_v – постоянная, значение берется из справочника;

D – диаметр сверла;

q, у, m – показатели степени для конкретных условий обработки;

Т- средний период стойкости, мин;

S – подача, мм/об;

K_v – суммарный поправочный коэффициент, учитывает фактические условия резания, данные берутся из таблиц.

C_v = 17,1; q_v = 0,25; y_v = 0,4; m = 0,125 – при S_о > 0,3 мм/об и без охлаждении (табл. 28, [2], стр. 278);

T – период стойкости сверла, для сверла диаметром D = 19 мм при обработке чугуна сверлом из быстрорежущей стали принимаем T=45 мин (табл. 30, [2], стр. 279);

Общий поправочный коэффициент:

(2) 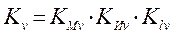, ([2], стр. 276)

K_Мv – поправочный коэффициент, учитывающий обрабатываемый материал;

K_Иv – поправочный коэффициент, учитывающий материал инструмента;

K_lv – поправочный коэффициент, учитывающий глубину сверления

(3) , (табл. 1, [2], стр. 261)

n_v – показатель степени;

HB - твердость обрабатываемого материала, МПа.

n_v = 1,3 (табл. 2, [2], стр. 262); σ_в = 180 МПа.

,

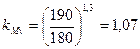K_Иv – поправочный коэффициент, учитывающий материал инструмента, для сверла из быстрорежущей стали Р18 принимаем K_Иv = 1,0 (табл. 6, [2], стр. 263);

K_lv – поправочный коэффициент, учитывающий глубину сверления, принимаем K_lv = 1,0 (табл. 31, [2],стр. 280);

,

.

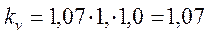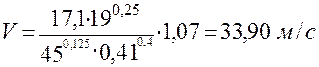2.3 Определяем осевую составляющую силы резания по формуле:

(4) 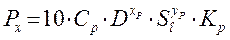, ([1], стр. 13)

С_р – постоянная, значение берется из справочника;

х, у– показатели степени для конкретных условий обработки для каждой из составляющих силы резания;

S – подача, мм/об;

D – диаметр сверла, м/с;

k_р – суммарный поправочный коэффициент, учитывает фактические условия резания, данные берутся из таблиц

C_P = 42,7; q_P = 1,0; y_P = 0,8 (табл. 32, [2], стр. 281);

K_P – поправочный коэффициент на осевую составляющую силы резания

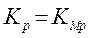, ([2], стр. 280)

(5) , ([2], стр. 264)

n_p – показатель степени;

HB - твердость обрабатываемого материала, МПа.

n_P = 0,6 (табл. 9, [2], стр. 264).

,

,

.

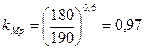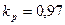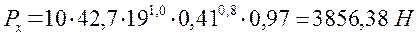2.4 Определяем момент сил сопротивления резанию (крутящий момент) по формуле:

(6) 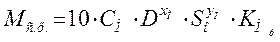, ([1], стр. 13)

С_M – постоянная, значение берется из справочника;

х, у– показатели степени для конкретных условий обработки для каждой из составляющих крутящего момента;

S – подача, мм/об;

D – диаметр сверла, м/с;

K_MP – поправочный коэффициент на осевую составляющую силы резания

C_M = 0,021; q_M = 2,0; y_M = 0,8 – для серого чугуна с пределом прочности σ_в = 180 МПа (табл. 32, [2], стр. 281);

.

,

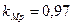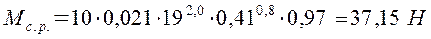2.5 Определяем номер конуса Морзе хвостовика.

Момент трения между хвостовиком и втулкой определяется по формуле:

(7) 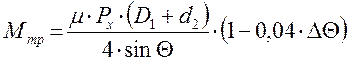, ([1], стр. 13)

Р_х – осевая сила, Н;

μ– коэффициент трения стали по стали;

θ– половина угла конуса;

D₁ ,d₂ – диаметры конуса хвостовика, мм.

Приравниваем момент трения к максимальному моменту сил сопротивления резанию, т. е. к моменту, создающемуся при работе затупившимся сверлом, который увеличивается до 3 раз по сравнению с моментом, принятым для нормальной работы сверла.

Следовательно, 3×М_с.р. = М_тр .

Средний диаметр конуса хвостовика определяется по формуле: d_ср = (D₁ + d₂)/2,

(8) 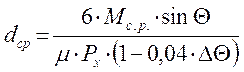, ([5], стр. 192)

М_ср – момент сопротивления сил резанию, Н·м;

Θ = 1^о26'16'' – половина угла конуса (конусность равна 0,05020; sin Θ = 0,0251), ([1], стр. 14);

Р_х – осевая сила, Н;

μ = 0,095 – коэффициент трения стали по чугуну ([1], стр. 14);

∆Θ = 5' – отклонение угла конуса ([1], стр. 14).

,

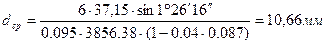По ГОСТ 25557 – 82 выбираем ближайший больший конус, т. е. конус Морзе № 2 с лапкой ([2] стр. 150), со следующими основными конструктивными размерами: D₁ = 18 мм; d₂ = 14 мм; l₃ = 75 мм; l₄ = 80 мм.

2.6 Определяем длину сверла.

Общую длину сверла L, длину рабочей части l_о, длину хвостовика l_х и длину шейки l₂ принимаем по ГОСТ 2092 – 77 (табл. 40, [2], стр. 137).

(9) L = l_о + l_х + l₂ = 52 + 65 + 16 = 133 мм.

L - общая длина сверла, мм;

l_о - длина рабочей части, мм;

l_х - длину хвостовика l_х, мм;

l₂ - длину шейки, мм.

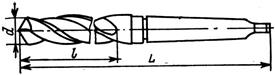
Рис. 2. Сверло спиральное с коническим хвостовиком

2.7 Определяем геометрические и конструктивные параметры рабочей части сверла.

Форму заточки принимаем ДП (двойная с подточкой поперечной кромки) (табл. 43, [2], стр. 151). Принимаем данный вид заточки, т.к обрабатываемый материал - чугун, а ДП используется для обработки чугунов с неснятой коркой, данная заточка позволяет значительно увеличить стойкость сверла и увеличить скорость резания.

Угол наклона винтовой канавки ω = 31°. Углы между режущими кромками: 2φ = 118°; 2φ_о = 70°. b = 2,5 мм. Задний угол α = 12°. Угол наклона поперечной кромки ψ = 55°. Размеры подточенной части перемычки: a = 1,5 мм, l = 2,5 мм. Шаг винтовой канавки:

(10) H = π × D/tg ω = 3,14 × 19/tg30° = 103,33 мм.

H - шаг винтовой канавки, мм;

D- диаметр сверла, мм;

ω - угол наклона винтовой канавки, °.

Центровочное отверстие принимаем формы А ГОСТ 14034 – 74.

Форма A

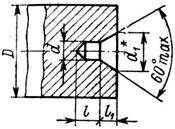
Рис. 3 Центровочное отверстие с углом конуса 60°

D = 14 мм, d = 2 мм, d₁ = 4 мм, l = 2,5 мм, l₁ = 1,5 мм.

2.8 Толщину сердцевины сверла выбираем в зависимости от диаметра сверла. Для сверла диаметром D = 19 мм толщину сердцевины у переднего конца принимаем:

(11) d_с = 0,14 × D = 0,14 × 19 = 2,66 мм , ([1], стр. 14)

D- диаметр сверла, мм;

d_с - толщина сердцевины сверла, мм.

Принимаем это утолщение равным 3 мм.

2.9 Обратную конусность сверла (уменьшение диаметра по направлению к хвостовику) на 100 мм длины рабочей части для сверла диаметром D = 19мм принимаем равной 0,12 мм ([1], стр. 14).

2.10 Ширину ленточки (вспомогательной задней поверхности лезвия) f_о и высоту затылка по спинке K выбираем в соответствии с диаметром сверла D. Принимаем f_о = 0,2 мм; K = 0,9 мм (табл. 44, [2], стр. 151).

2.11 Ширина пера:

(12) B = 0,38 × D = 0,38 × 19 = 7,22 мм , ([1], стр. 14)

D- диаметр сверла, мм;

В – ширина пера, мм.

2.12 Геометрические элементы профиля фрезы для фрезерования канавки сверла определяем упрощенным аналитическим методом.

Больший радиус профиля:

(13) 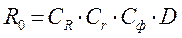, ([5], стр. 193)

,

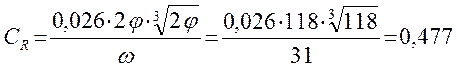(14) ,

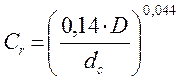при отношении толщины сердцевины d_с к диаметру сверла D, равном 0,14, C_r = 1;

(15) ,

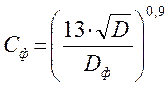D_ф – диаметр фрезы.

При D_ф = 13 × ÖD, C_ф = 1.

Следовательно, R₀ = 0,477 × 1 × 1 × 19 = 9,063 мм.

Меньший радиус профиля R_к = C_к × D, где

C_к = 0,015 × ω^0,75 = 0,015 × 31^0,75 = 0,197.

Следовательно, R_к = 0,197 × 19= 3,743 мм.

Ширина профиля B = R₀ + R_к = 9,063 + 3,743 = 12,806 мм.

2.13 Устанавливаем основные технические требования и допуски на размеры сверла (по ГОСТ 885 – 77*).

Предельные отклонения диаметров сверла D = 19h9_(-0,043) мм. Допуск на общую длину и длину рабочей части сверла равен удвоенному допуску по 14-му квалитету с симметричным расположением предельных отклонений 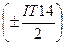по ГОСТ 25347 – 82. Предельные отклонения размеров конуса хвостовика устанавливают по ГОСТ 2848 – 75* (степень точности AT8). Радиальное биение рабочей части сверла относительно оси хвостовика не должно превышать 0,15 мм. Углы 2φ = 118° ± 2°; 2φ₀ = 70°^+5°. Угол наклона винтовой канавки ω = 31°_-2°.

Предельные отклонения размеров подточки перемычки режущей части сверла +0,5 мм. Твёрдость рабочей части сверла 63 – 66 HRC_э, у лапки хвостовика сверла 32 – 46,5 HRC_э.