Вопрос 53. проверочный расчёт валов на статическую прочность, жесткость и колебания

Проверку статической прочностипроизводят в целях предупреждения пластических деформаций и разрушений с учетом кратковременных перегрузок (например, пусковых и т. п.). При этом определяют эквивалентное напряжение по формуле

где

Здесь М и Т ‑ изгибающий и крутящий моменты в опасном сечении при перегрузке.

Расчет на жесткость. Упругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колес, катков фрикционных передач и т. п.

От прогиба вала в зубчатом зацеплении возникает концентрация нагрузки по длине зуба. При больших углах поворота в подшипнике может произойти защемление вала.

Допускаемые упругие перемещения зависят от конкретных требований к конструкции и определяются в каждом отдельном случае. Приближенные рекомендации следующие:

Для вала зубчатых передач стрела прогиба под колесом ‑ передачи цилиндрические; ‑ конические, гипоидные, глобоидные передачи, где т ‑ модуль зацепления.

Угол взаимного наклона валов под шестернями рад.

В станкостроении для валов общего назначения ,

где ‑ расстояние между опорами.

Угол поворота вала в подшипнике скольжения 0,001 рад; в радиальном шарикоподшипнике 0,005 рад.

Малые величины допускаемых перемещений иногда приводят к тому, что размеры вала определяет не прочность, а жесткость. В этих случаях нецелесообразно изготовлять вал из дорогих высокопрочных сталей (если это не диктуется какими-либо другими условиями, например износостойкостью цапф).

Перемещение при кручении валов постоянного диаметра определяют по формуле

где ‑ угол закручивания вала, рад;

‑ крутящий момент;

‑ модуль упругости при сдвиге;

‑ длина закручиваемого участка вала;

‑ полярный момент инерции поперечного сечения вала.

Если вал ступенчатый и нагружен несколькими , то угол определяют по участкам и затем суммируют.

Расчет на колебания.

На валу, вращающемся с угловой скоростью закреплен диск массой 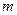с эксцентриситетом е. Собственную массу вала считаем малой по сравнению с т и в расчет не принимаем (упругая система с одной степенью свободы). На вал действует центробежная сила вектор которой вращается с угловой скоростью .

Составляющие силы F, по осям у и z:

Силы F_y и F_z являются гармоническими возмущающими силами, которые вызывают изгибные колебания вала в направлении осей у и z.

Колебания от силы F_y описываются уравнением:

Колебания от силы F_z описываются уравнением:

Частота собственных изгибных колебаний

где ‑ изгибная податливость вала или прогиб от единичной силы;

‑ статический прогиб вала от действия силы тяжести mg диска.

Анализируя уравнение колебаний позволяет отметить, что при

При наступает резонанс.

Таким образом, даже при ничтожно малой неуравновешенности в условиях резонанса можно ожидать разрушения машины.

Частоту вращения (мин^-1), при которой наступает резонанс, называют критической: