Прямоугольные изометрические проекции

Кафедра «Профессиональное обучение, инженерная графика и САПР»

В.А. Садовая

Проекционное черчение

Аксонометрические проекции

Учебно-методическое пособие по изучению дисциплины

Для студентов инженерных специальностей

Барнаул 2015

УДК 744 (072)

Садовая В.А. Инженерная графика. Проекционное черчение. Аксонометрические проекции. Методическое пособие по изучению дисциплины для студентов инженерных специальностей. / В.А. Садовая. - Барнаул: РИО Алтайский ГАУ, 2015. – 21с.

Учебно-методическое пособие содержит методические указания по изучению дисциплины «Начертательная геометрия. Инженерная графика» и выполнению самостоятельных работ.

Пособие предназначено для сопровождения аудиторных практических занятий и самостоятельной работы студентов инженерных специальностей.

Рецензенты:

к.т.н., доцент кафедры «Начертательная геометрия и графика» АлтГТУ им. И.И. Ползунова Г.М. Кашкаров;

старший преподаватель кафедры «Механика машин и сооружений» ИФ Алтайский ГАУ И.Л. Новожилов.

Рекомендовано методической комиссией ИФ Алтайский ГАУ (протокол № 7 от 14.05. 2015 г.)

Ó Садовая В.А., 2015

Ó ФГОУ ВО Алтайский ГАУ, 2015

Цель и задачи пособия

Целью настоящего издания является изучение правил построения аксонометрических проекций деталей – ГОСТ 2.317- 2011. Получение навыков в построении наглядных изображений в аксонометрии необходимо при выполнении заданий по проекционному и машиностроительному черчению.

Методические указания

Изготовление деталей различных машин и инженерных сооружений производится по чертежам, выполненных методом ортогональных проекций при необходимости дополненными вспомогательными видами, разрезами и сечениями. Однако эти изображения имеют существенный недостаток, заключающийся в отсутствии наглядности, поэтому приходится одновременно рассматривать несколько проекций, что затрудняет мысленное воспроизведение предмета.

Наглядное изображение предмета достигается с помощью метода аксонометрических проекций.

Аксонометрической проекцией называется изображение предмета на некоторой плоскости, полученное параллельным проецированием, направление которого не совпадает с направлением координатных осей, ориентирующих проецируемый предмет.

В зависимости от направления проецирующих прямых и искажения линейных размеров предмета аксонометрические проекции делятся на прямоугольные и косоугольные. Если проецирующие прямые перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной аксонометрической проекцией. При направлении проецирования, не перпендикулярном к аксонометрической плоскости проекций, получают косоугольные аксонометрические проекции.

В зависимости от соотношения коэффициентов искажения как прямоугольные, так и косоугольные аксонометрические проекции разделяются на изометрические, диметрические и триметрические.

Изометрические проекции имеют по всем трём осям одинаковые коэффициенты искажения.

Диметрические проекции имеют по двум осям одинаковые коэффициенты искажения, а по третьей - отличный от первых двух.

Триметрические проекции по всем трём осям имеют разные коэффициенты искажения.

Теоретическое обоснование метода аксонометрических проекций дано в курсе начертательной геометрии. В черчении будем пользоваться «готовой» характеристикой аксонометрических изображений.

Рассмотрим наиболее распространенные – изометрические и диметрические проекции, рекомендуемые ГОСТ 2.317- 2011 для выполнения наглядных изображений и технических рисунков деталей.

Прямоугольные изометрические проекции

Прямоугольной изометрией называется аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120°. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.

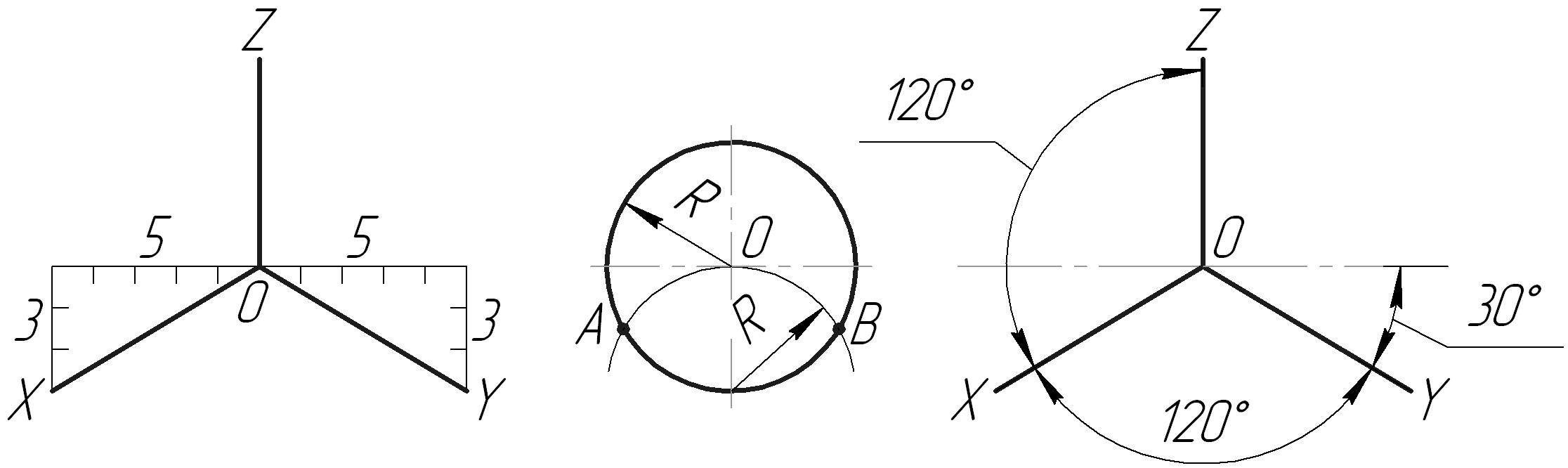
а) б) в)

Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.

При практических построениях коэффициент искажения (К) по аксонометрическим осям согласно ГОСТ 2.317- 2011 рекомендуют равный единице. При этом изображение получают более крупным по сравнению с теоретическим или точным изображением при коэффициентах искажения 0,82. Увеличение равно 1,22. На рис. 2 приведён пример изображения детали в прямоугольной изометрической проекции.

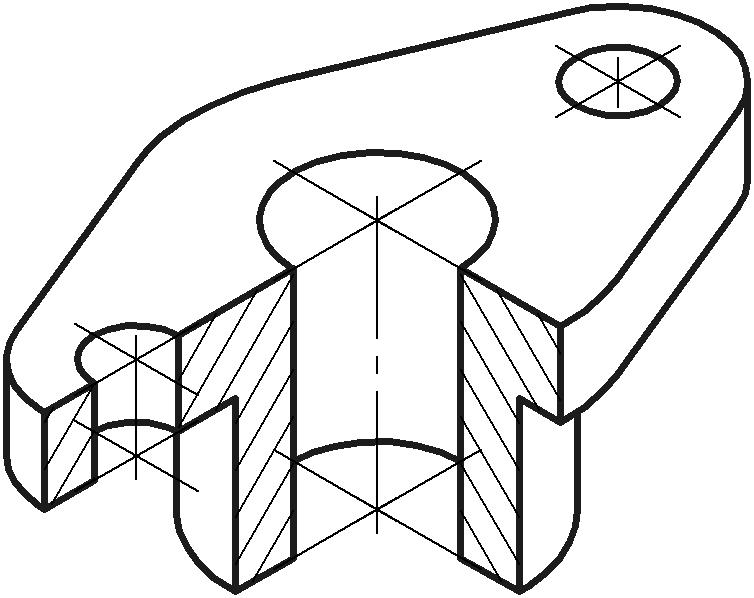
Рис. 2. Изометрия детали.