Коэффициенты формы зуба червячного колеса

Zv2
YF2	2,43	2,41	2,32	2,27	2,22	2,19	2,12	2,09	2,08	2,04

Пример выполнения практической работы № 3

Рассчитать червячную передачу одноступенчатого редуктора и проверить зубья червячного колеса на прочность по контактным напряжениям и напряжениям изгиба, если мощность на валу червяка – Р₁=8 кВт, угловая скорость ведущего вала – ω₁ = 140 рад/с, передаточное число u = 30. Червяк выполнен из закалённой стали 40Х с твёрдостью витков HRC > 45. Редуктор нереверсивный, предназначен для длительной работы при постоянной нагрузке. Положение червяка - верхнее.

Решение

1. Выбираем марку материала для венца червячного колеса, для чего определяем скорость скольжения по формуле

V_s= ,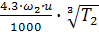

где ω₂ = ω₁/u = 140/40 = 3,5 рад/с;

Т₂ = 10³Р/ ω₂ - 8000/3,5 = 2286 Нм.

Тогда V_s = 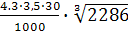= 5,9 м/с.

По табл. 3.1 выбираем бронзу Бр05Ц5С5, имеющую следующие характеристики: σ_в = 200 Н/мм², σ_т = 90 Н/мм².

2. Допускаемые контактные напряжения:

[σ_H] = 0,9C_vσ_B = 0,9·0,89·200 = 160 Н/мм².

Так как червяк расположен вне масляной ванны, то [σ_H] уменьшаем на 15%: [σ_H] = 160·0,85 = 136 Н/мм²

Допускаемые изгибные напряжения:

[σ_F] = 0,08 σ_B + 0,25 σ_T = 0,08·200 + 0,25·90 = 38,5 Н/мм².

3. Межосевое расстояние:

α_w=61· 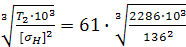=304 мм.

По стандарту принимаем α_w =315 мм.

4. Принимаем число витков червяка z₁. Для u = 30, z₁ = 2.

5. Число зубьев червячного колеса z₂ = z₁·u = 2·30 = 60.

6. Модуль зацепления:

m = (1,5…1,7)α_w/z₂ = (1,5...1,7)315/60 = 7,9.. .8,9.

По стандарту принимаем m = 8 мм.

7. Коэффициент диаметра червяка

q = (0,212...0,25)z₂= 12,7 ... 15.

Принимаем q= 14.

8. Коэффициент смещения инструмента:

х = (α_w/m)-0,5(q + z₂) = 315/8-0,5(14+60) = 2,4>1

Увеличиваем число зубьев колеса: z₂ = 61.

Принимаем коэффициент диаметра червяка q = 16.

Тогда х = 315/8-0,5(16+61) = 0,9.

9. Фактическое передаточное число u_ф = z₂/z₁ = 61/2 = 30,5.

Отклонение от заданного 100%( u_ф - u)/u = 100%(30,5 - 30)/30 = 1,7%.

10.Фактическое значение межосевого расстояния

α_w = 0,5m(q + z₂ + 2х) = 0,5·8(16 + 61 + 2·0,9) = 315,2 мм

11. Основные геометрические размеры передачи:

а) червяка:

делительный диаметр d₁ = qm = 16·8 = 128 мм

начальный диаметр d_wl = m(q + 2х) = 8(16 + 2·0,9) = 142,4 мм

диаметр вершин витков d_a1 = d₁ + 2m =128 + 2·8 = 144 мм

диаметр впадин витков d_f1 = d₁ – 2,4m = 128 – 2,4·8 = 108,8 мм

угол подъёма линии витков γ = arctg(z₁/q) = arctg(2/l6)=7°7'

длина нарезаемой части червяка

b₁ = (10+5,5|x|+z₁)m+100m/z₂ = (10 + 5,5·0,9 + 2)8 + 100·8/61 = 148,7 мм;

б) венца червячного колеса:

делительный диаметр d₂ = mz₂ = 8·61= 488 мм

диаметр вершин зубьев d_a2 = d₂+2m(l+x) = 488+2·8(1+0,9) = 518,4мм

наибольший диаметр колеса

d_aM2 ≤ d_a2 + 2m(l + х)=518,4+2·8(1+0.9)=548,8 мм

диаметр впадин зубьев d_f2 = d₂-2m(1,2-x) = 488-2·8(1,2-0,9)=483,2 мм

ширина венца b₂ = 0,355α_w = 0,355∙315,2 = 111,9 мм

условный угол обхвата червяка венцом колеса 2δ:

Sin δ = b₂/(d_a1 – 0,5m) =111,9/(144 – 0,5 · 8) = 0,7993 δ = 53°3'.

Угол должен быть в пределах 90...120 градусов.

12. Фактическая скорость скольжения V_s = 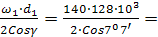9 м/с.

Угол трения φ=1°.

Коэффициент полезного действия червячной передачи

η= .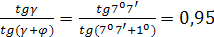

13. Окружная сила на колесе F_t2 = 2T₂·10³/d₂ = 2·2286·10³/488 = 9369 Н.

Окружная скорость на колесе v₂ = ω₂d₂/2000 = 3,5·488/2000 = 0,85м/с.

Тогда коэффициент нагрузки К=1.

Контактные напряжения зубьев колеса:

σ_Н=340 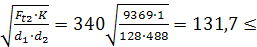[ σ_Н].

Условие прочности выполняется.

14. Напряжения изгиба зубьев колеса

σ_F=0,7Y_F2 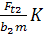≤ [σ_F].

Здесь Y_F2 зависит от z_v2 = z₂/cos³γ = 61/cos³7°7' = 62. Тогда YF2 = 2,14.

Тогда σ_F =0,7·2,14·9369·1/(111,9·8)= 15,7 ≤ [σ_F].

Условие прочности выполняется.

Таблица 3.6

Варианты заданий для практической работы