Последовательность выполнения работы. 4.1.Вычертить схему установки

4.1.Вычертить схему установки.

4.2.Проверить правильность положения задвижек и вентилей.

4.3.Определить удельную энергию положения в характерных сечениях, приняв за плоскость сравнения пол лаборатории или ось трубопровода (если она горизонтальна).

4.4.Определить площади характерных сечений wпо заданным внутренним диаметрам трубопровода.

4.5.Вкючить центробежный насос (ВКЛЮЧАЕТ ЛАБОРАНТ ИЛИ ПРЕПОДАВАТЕЛЬ), установить постоянный уровень в напорном резервуаре, проверить уровни в пьезометрах, открыть регулировочный кран 4.

4.6.Снять показания пьезометров в характерных сечениях при установившемся движении, определить время наполнения мерного бака (дважды) объемом W. Включить центробежный насос.

4.7.Вычислить расход воды (Q) объёмным способом.

4.8.Вычислить средние скорости в характерных сечениях, используя уравнение постоянства расхода

.

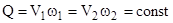4.9.Вычислить удельную кинетическую энергию ( 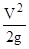), удельную потенциальную ( 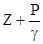), полную ( 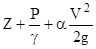), удельную энергию (в каждом характерном сечении) и потери полной удельной энергии (h_1-2) как между соседними сечениями, так и по всей длине опытного участка трубопровода.

4.10. Вычислить пьезометрическую линию и линию полной удельной энергии в масштабах: M 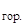= 1:20. М 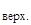= 1:5 на отдельном листе миллиметровки.

4.11.Результаты вычислений свести в таблицу 1.

5. Контрольные вопросы

5.1.Что такое удельная энергия жидкости?

5.2.Как называется каждый член уравнения Бернулли?

5.3.В каких единицах измеряется каждый вид удельной энергии жидкости?

5.4.Какими методами определяется величина различных видов удельной энергии жидкости?

5.5.Из каких составляющих складываются общие потери удельной энергии на участке потока?

Литература

6.1.Кедров В.С., Калицун В.И. Гидравлика, водоснабжение и канализация. М., Стройиздат 1972 г., стр.44-49.

6.2.Угинчус А.А. Гидравлика и гидравлические машины. Харьков 1970 г., стр.111-130.

6.3.Башта Т.М. Гидравлика, гидравлические машины и гидропривод. М., Машиностроение, стр. 44-52.

Таблица результатов

Определяемые величины	№№	№№ пьезометров
P/γ	сред.
z
z+P/γ
V2/2g
e=z+P/γ+V2/2g
h1-2
h1-7

ЛАБОРАТОРНАЯ РАБОТА №3

Тарирование водомера Вентури

Цель работы

Получение опытным путем значений коэффициента расхода при различных измеряемых расходах, построение графика зависимости от критерия Рейнольдса и определение величины коэффициента расхода в квадратичной зоне.

Введение

Водомер Вентури, схема которого изображена на рис.1, состоит из конусообразной сходящейся трубки со вставкой меньшего диаметра, чем диаметр цилиндрической трубы, к которой присоединяется водомер. За вставкой следует конус водомера, расширяющийся в направлении течения. По оси прибора устанавливаются два пьезометра: один перед началом конусообразного сужения, а другой посередине суженной вставки.

Обозначим:

D₂- диаметр трубки, в которой производится измерение расхода жидкости;

D₃- диаметр суженной вставки;

V₂- средняя скорость в трубе диаметром D₂;

V₃- средняя скорость в области суженной вставки.

Применим уравнение Бернулли к потоку жидкости, движущейся по водомеру Вентури. Для этого проведем плоскость сравнения 0-0 по оси прибора и рассмотрим два сечения: сечение 2-2 в начале сужения, где установлен первый пьезометр, и сечение 3-3 суженной вставки, где установлен второй пьезометр.

Вследствие незначительной длины прибора между указанными сечениями (обычно 3-5 диаметров трубы) и плавного конусообразного подхода к суженной вставке, потерями энергии можно пренебречь. Поэтому можем записать уравнение Бернулли применительно к рассматриваемому случаю следующим образом:

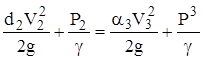. (1)

Геометрические высоты z₁ и z₂ равны нулю вследствие того, что плоскость сравнения проходит через центры тяжести живых сечений, совпадающие с осью прибора. Так как расход равен

,

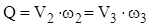то скорость V₃ определяется по формуле

.

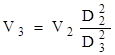Подставим полученное значение V₃ в уравнение (1), обозначим разность пьезометрических высот, отсчитываемую по шкале прибора через 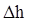.Тогда

,

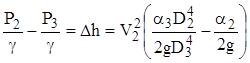следовательно,

.

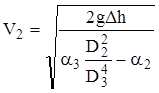С другой стороны, расход жидкости, проходящей через водомер, равен:

.

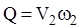Поэтому:

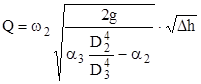. (2)

При выводе зависимостей (2) мы не учитывали потерь энергии при движении воды через прибор. Практически эти потери учитываются введением коэффициента расхода водомера m. Следовательно, окончательная формула для расхода жидкости, проходящей через водомер, будет иметь следующий вид:

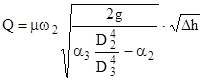
Таким образом, для определения расхода жидкости с помощью водомера рассматриваемой конструкции надо знать постоянную прибора, зависящей от его размеров;

.

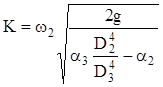Коэффициент расхода m=0,985 для новых водомеров и m=0,98 для водомеров бывших в употреблении.

При определении постоянной водомера, коэффициенты неравномерности a₂ и a₃ могут быть приняты равными 1. Кроме того, нужно иметь ввиду, как будет показано далее, что в некоторых случаях коэффициент расхода m может зависеть от числа Рейнольдса, т.е. .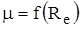

Следовательно, зная m и К необходимо только произвести отсчёт по пьезометрам. При этом показание второго пьезометра будет всегда меньше показания первого, так как в суженной части трубки скорости будут больше, а давление ниже. Таким образом, суженная вставка устраивается для получения разности пьезометрических высот.

Кроме рассмотренного выше водомера, для измерения расхода жидкости в трубах применяются измерительные шайбы (диафрагмы), расчёт которых также основан на уравнении Бернулли.

Измерительные приборы

Секундомер, мерный бак, пьезометры.

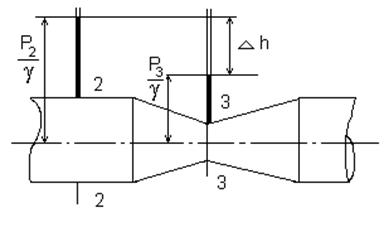Рис. 1. Водомер Вентури