Определение числа неизвестных
Вводимые в основную систему дополнительные связи имеют вид. моментной (угловой) связи, которая препятствует повороту узла, но не мешает линейной подвижности узла, или силовой (поступательной) связи, которая препятствует только линейному перемещению узла. Угловые связи накладываются на все жесткие узлы, системы, а линейные — там, где есть независимые поступательные перемещения узлов.
На рис. 56, а показан неподвижный портал рамной конструкции, который служит основой для разнообразных типов кранов. В качестве нагрузки приняты полезная G и линейная q от ветра. Дополнительные угловые связи для данной системы накладываются в узлах В и С. Для определения числа независимых линейных перемещений узлов рамы подсчитывается степень упругой подвижности системы П. Определение ее для рам базируется на следующих допущениях, принятых в МП: 1) концы стержней, соединенных жестко в узле, поворачиваются на один и тот же угол, т. е. угол между стержнями при деформации не меняется; 2) не учитывается влияние продольных N и поперечных Q сил на перемещения узлов; 3) расстояния между узлами при изгибе прямых стержней не меняются; 4) углы поворота вследствие малых значений принимаются равными их тангенсам.
Для рамы (рис. 56, а) изобразим шарнирную схему (рис. 56, б) путем установки шарниров в узлах В и С. Степень упругой подвижности равна П=ЗС – 2Ш, где С — число стержней рамы; 3 — число степеней свободы стержня на плоскости; Ш — число простых шарниров; 2 — число связей, накладываемых простым шарниром. Для рассматриваемого случая П = 3 × 3 — 2 × 4 = 1, т. е. имеем одно независимое поступательное (линейное) перемещение узлов В и С по горизонтали. Следовательно, необходимо -ввести одну дополнительную связь, например в узле В, препятствующую этому перемещению. Число независимых поступательных перемещений равно числу дополнительных связей, обращающих шарнирную схему в геометрически неизменяемую. Перемещениями узлов В и С по вертикали вследствие продольных деформаций стержней пренебрегаем.
На рис. 56, в показана основная система. по МП, имеющая пу = 2 — число угловых связей и пл =1 — число линейных связей. Степень кинематической неопределимости по МП равна kп = nу + nл. Для этой же рамы при расчете по МС степень статической неопределимости сН = 1. В общем случае kH ≠ cH .
На рис. 57показана безраскосная ферма мостового крана. Для этой фермы сН = 3п = =3×7 = 21, где п — число замкнутых контуров. Величина kH = 16 + 7 = 23. Основная система (рнс. 56, в) представляет собой сочетание стандартных элементов — балки ВС, защемленной по концам, и балок АВ и СD, защемленных на одном конце и шарнирно опертых — на другом. Решения для некоторых стандартных балок при действии нагрузки и смещении их концов, в том числе для балок, из которых образуются основные системы по рис. 56, в, приведены в табл. 2. Отсюда следует, что основная система МП может быть получена единственным способом.
|
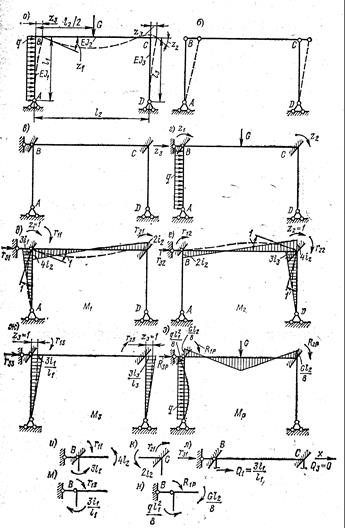
а – схема нагрузки на портал; б – шарнирная схема рамы портала; в – основная система по МП; г – система, эквивалентная заданной; д, е, ж – единичные эпюры М1 – М3; з – грузовая эпюра; и – равновесие узла В при Z1 = 1; k – равновесие узла С при Z1 = 1; л – равновесие стержня ВС при Z1 = 1; м – равновесие узла В при Z3 = 1; н – равновесие узла В при учете действия внешней нагрузки.
Рисунок 56 – К расчету неподвижного портала методом перемещений.
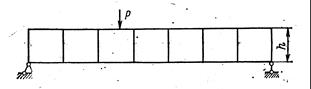
Рисунок 57 – Безраскосная ферма мостового крана
В этом главное преимущество МП по сравнению с МС, что особенно существенно при расчете на ЭВМ. Для устранения противоречий между заданной системой (см. рис.56, а) и основной (см. рис. 56, в) переместим каждую дополнительную связь последней на величину перемещения z1, z2, z3 в заданной. Эти перемещения приводят к возникновению реакций, наложенных связей. От действия нагрузки в этих же связях также имеют место реакции. Так, в i-и связи суммарная реакция Ri (z1, z2, z3, Р) является функцией перемещений z1, z2, z3 и нагрузки Р. Эта реакция равна нулю, если в заданной системе в рассматриваемом узле не приложено никакой силы в направлении дополнительной связи. При этом основная система с наложенными связями (см. рис.56, г) эквивалентна заданной. Полагая, i = 1, 2, 3, получим три уравнения равновесия:
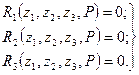 (106)
(106)
Далее решаем систему уравнений (106) относительно z1, z2, z3.