Лекция № 8. Тема: «Уравнения Бернулли для элементарной струйки и потока вязкой жидкости»
Полный напор в любом сечении струйки вязкой жидкости определяется теми же составляющими, что и для невязкой жидкости. Однако значение полного напора в сечениях будет разное, так как часть энергии в вязкой жидкости расходуется на преодаление гидравлических сопротивлений (трение частиц друг о друга, о стенки). При этом часть гидравлической энергии преобразуется в тепловую или механическую (колебание трубопровода) и рассеивается во внешнюю среду. Следовательно, напор в сечении II-II (рис.8.1) будет меньше, чем в сечении I-I на величину потерь напора.
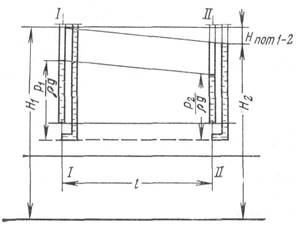
Рисунок 8.1 Графическое определение потерь напора
Последние определяются как разность полных напоров в соответствующих сечениях 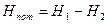 . Отсюда, если
. Отсюда, если 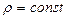 , получим уравнение Бернулли для струйки вязкой жидкости
, получим уравнение Бернулли для струйки вязкой жидкости
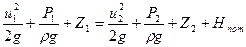 ; (8.1)
; (8.1)
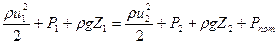 . (8.2)
. (8.2)
Левые члены уравнений (8.1) и (8.2) дают соответственно полный напор, полное давление, полный запас удельной энергии элементарной струйки в сечении I-I относительно принятой плоскости сравнения.
Основное различие уравнений Бернулли для потока и элементарной струйки заключается в определении скоростного напора в живом сечении. В отличие от элементарной струйки скорости частиц жидкости в различных точках живого сечения потока неодинаковы, поэтому при определении кинетической энергии через среднюю скорость допускается неточность, которую необходимо учесть.
Кинетическая энергия жидкости в сечении элементарной струйки
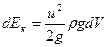 , (8.3)
, (8.3)
где 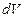 - элементарный объем жидкости, проходящий через живое сечение струйки за время
- элементарный объем жидкости, проходящий через живое сечение струйки за время 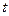 ;
; 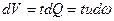 . Тогда
. Тогда
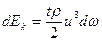 .
.
Для потока запас кинетической энергии будет 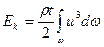 и скоростной напор
и скоростной напор
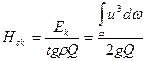 . (8.4)
. (8.4)
Скоростной напор, выраженный через среднюю скорость 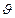 (6.4), не равен действительному значению, найденному по уравнению (8.4). Отношение действительного скоростного напора к подсчитанному по средней скорости называется коэффициентом Кориолиса:
(6.4), не равен действительному значению, найденному по уравнению (8.4). Отношение действительного скоростного напора к подсчитанному по средней скорости называется коэффициентом Кориолиса:
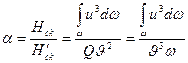 . (8.5)
. (8.5)
Для равномерного турбулентного потока 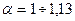 , для равномерного ламинарного потока
, для равномерного ламинарного потока 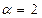 . На участках неравномерного движения вследствие искажения поля скоростей коэффициент
. На участках неравномерного движения вследствие искажения поля скоростей коэффициент 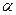 может иметь различные значения, достигающие 5 и более единиц. Если в уравнениях (8.1) и (8.2) вместо местной скорости
может иметь различные значения, достигающие 5 и более единиц. Если в уравнениях (8.1) и (8.2) вместо местной скорости 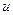 подставить среднюю скорость
подставить среднюю скорость 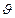 , введя поправку к скоростному напору
, введя поправку к скоростному напору 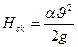 , получим уравнение Бернулли для потока
, получим уравнение Бернулли для потока
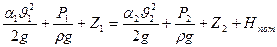 (8.6)
(8.6)
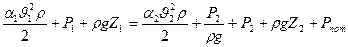 . (8.7)
. (8.7)
Рассеивание энергии, потери покрываются в основном за счет потенциальной энергии и могут быть выражены как потери напора 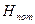 (8.6), потери давления
(8.6), потери давления 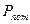 (8.7).
(8.7).
Для потока капельной жидкости (8.6) отношение потерь напора к длине потока (трубопровода) называется гидравлическим уклоном:
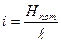 . (8.8)
. (8.8)
Гидравлический уклон – величина безразмерная, характеризующая потерю напора на единицу длины. В частности, для горизонтального равномерного потока 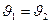 ;
; 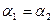 ;
; 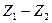 . Согласно уравнению (8.6), потери напора определяются изменением пьезометрического напора (рис.8.1) и поэтому гидравлический уклон
. Согласно уравнению (8.6), потери напора определяются изменением пьезометрического напора (рис.8.1) и поэтому гидравлический уклон
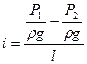 . (8.9)
. (8.9)
При решении многих инженерных задач необходимо знать мощность потока. Удельная энергия представляет работу, которую может выполнить единицу массы, объема или веса жидкости, а мощность равна работе единицу времени всей массы, объема или веса. Поэтому для получения мощности необходимо полные напоры умножить соответственно на расходы: массовый 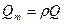 , объемный
, объемный 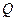 или весовой
или весовой 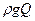 . В результате этого получим
. В результате этого получим
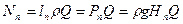 . (8.10)
. (8.10)
Размерность: 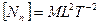 , единица в системе СИ -
, единица в системе СИ - 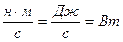 . Для перемещения вязкой жидкости необходимо вводить в поток энергию, которая должна покрыть рассеивание энергии, т.е. мощность, которую можно определить, если в уравнение (8.10) вместо полных напоров подставить
. Для перемещения вязкой жидкости необходимо вводить в поток энергию, которая должна покрыть рассеивание энергии, т.е. мощность, которую можно определить, если в уравнение (8.10) вместо полных напоров подставить 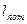 ,
, 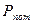 и
и 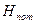 .
.
Литература:4 осн. [54-57]; 1 осн. [97-104]; 6доп. [44-48].
Контрольные вопросы
1. Напишите уравнение Бернулли для элементарной струйки и потока вязкой жидкости.
2. Что такое коэффициент Кориолиса и что он характеризует?
3.По каким формулам определяют мощность потока жидкости при объемном, массовом и весовом расходах?
