Нормальное приращение в горизонтально-слоистой среде
Скоростной анализ, статические поправки, суммирование
ВВЕДЕНИЕ
Данные АК представляют прямое измерение скорости, с которой сейсмические волны распространяются в разрезе в зависимости от глубины. Сейсмические данные, с другой стороны, обеспечивают непрямое измерение скорости. Основываясь на этих двух типах информации, сейсморазведчик получает большое количество различных типов скоростей, таких как интервальная, кажущаяся, средняя, среднеквадратичная, мгновенная, фазовая, групповая, по ОГТ, суммирования и миграции. Однако, наиболее достоверная скорость, получается по сейсмическим данным. Это та, которая дает лучшую сумму. Если предположить, что разрез является сложным, скорость суммирования относится к скорости ОГТ, которая, в свою очередь, относится к среднеквадратичной скорости (ур. 3.4), из которой выводятся средняя и интервальная скорости.
Интервальная скорость – это средняя скорость в интервале между двумя отражающими поверхностями. В блоке пород с определенным литологическим составом на интервальную скорость влияют несколько факторов:
1. 1. Форма пор
2. 2. Поровое давление
3. 3. Насыщенность порывами флюидами
4. 4. Ограничивающее (горное) давление
5. 5. Температура
Эти факторы подверглись обширным исследованиям в лабораторных условиях. На рис.3.1 показана скорость, измеряя в лаборатории в зависимости от горного давления на образе известняка Bedford с порами в форме микротрещин. Эксперимент проводился с образцами, заключенными в корпус, чтобы управлять давлением поровых флюидов независимо от горного давления. При возрастании горного давления увеличивались скорости как продольных, так и поперечных волн. Более определенно: скорость быстро возрастает с увеличением горного давления при малых его значениях, а затем постепенно выравнивается при дальнейшем росте горного давления (рис.3.1). Причина этого заключается в том, что при возрастании горного давления поры закрываются. Однако, при высоком поровом давлении деформируемого порового пространства не остается. Следовательно, дальнейший рост горного давления не приводит к значительному увеличению скорости. Из рис.3.1 видно, что скорость Р-волн больше скорости S-волн независимо от горного давления. Это справедливо для любого типа породы. Наконец, на рис.3.1 можно видеть действие флюидонасыщенности в порах. Насыщенный образец характеризуется более высокой скоростью Р-волн, чем сухой образец при низком горном давлении (почему так?). При высоких значениях горного давления скорость Р-волн в сухом образце приближается к величине скорости Р-волн в насыщенном образце. Отметим также, что скорость Р-волн в насыщенном образце не изменяется так же быстро, как в сухом образце, поскольку флюид почти так же несжимаем, как порода. Скорость S-волн мало зависит от того, заполнены поры флюидом или нет, т.к. флюиды не могут поддерживать распространение поперечных волн.
Теперь исследуем скорость в функции горного давления для образца песчаника Berea с круглыми порами, заключенного в корпус (рис.3.2). Снова можно видеть возрастание скорости с увеличением горного давления. Существенное различие между этим образцом и образцом на рис.3.1 состоит в диапазоне изменения скорости. При любом данном горном давлении порода с микротрещинами характеризуется более высокой скоростью, чем порода с круглыми порами. Причина состоит в том, что легче закрыть поры в виде микротрещин, чем круглые поры. Наиболее заметное влияние на скорость в породе с данной литологией и пористостью оказывает, вероятно, горное давление. Этот тип давления вызван перекрывающими отложениями и увеличивается с глубиной. Скорость также увеличивается с глубиной. Однако, поскольку существуют такие факторы как поровое давление, может иметь место инверсия скорости в слое. На рис.3.3 показано изменение скорости с глубиной для различных типов литологии. Третичные обломочные породы, которые имеют меньший возраст, чем другие породы, занимают низкоскоростную часть графика. Они начинаются со скорости, которая изменяется от 1.5 до 2.5км/с на поверхности или вблизи нее, а затем постепенно увеличиваются до 4.5 – 5.5км/с на глубинах более 5км. Карбонаты с высокой пористостью занимают среднюю часть графика, для них скорость возрастает от 3 до 6км/с. С другой стороны, низкопористые карбонаты характеризуются меньшим диапазоном изменения скорости. Если в породе больше нет пор, которые могут быть закрыты, увеличение горного давления не дает повышения скорости.
В этой части главы рассматриваются способы оценки скоростей по сейсмическим данным. Для оценки скорости требуются данные, зарегистрированные при нулевых выносах. Имея оцененные скорости, мы можем внести поправку за нулевой вынос и сжать объем зарегистрированных данных (в координатах средняя точка – вынос – время) в суммированный разрез (рис.1.34).
Для одного горизонтального слоя с постоянной скоростью кривая времен пробега в функции выноса представляет собой гиперболу (Раздел 3.2). Разность времен пробега при данном выносе и при нулевом выносе называется нормальным приращением. Скорость, необходимая для ввода поправки за нормальное приращение, скоростью нормального приращения (NMO velocity).Для одной горизонтальной отражающей поверхности скорость нормального приращения равна скорости в среде над отражающей поверхностью (ОП). Для наклонной ОП эта скорость равна скорости в среде, деленной на косинус угла наклона. При наблюдении наклонной ОП в трех измерениях дополнительным фактором становится азимут (угол между направлением падения и направлением профиля). Зависимость времени пробега от выноса для последовательности плоских горизонтальных слоев с постоянной скоростью аппроксимируется гиперболой. При меньших высотах эта аппроксимация лучше, чем при больших выносах. Для малых выносов скорость нормального приращения для горизонтально-слоистого разреза среднеквадратичной скорости до границы рассматриваемого слоя. В среде, состоящей из слоев с произвольными наклонами уравнение времени пробега усложняется. Однако, на практике, если наклоны незначительные, а длина расстановки меньше глубины отражающей поверхности, можно считать, что время пробега аппроксимируется гиперболой. Для границ слов, формы которых произвольны, это допущение не действительно.
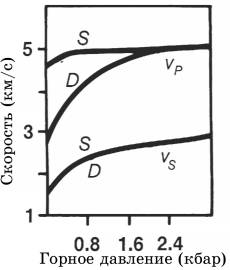 Рис.3.1 Изменение скоростей Р- и S-волн в зависимости от горного давления, наблюдаемое в сухих и водонасыщенных образцах известняка Bedford с порами в виде микротрещин. В течении замеров объем флюидов поддерживался постоянным. Здесь S = насыщенный, D = сухой, vP = скорость Р-волн, vS = скорость S-волн (Nur, 1981). Рис.3.1 Изменение скоростей Р- и S-волн в зависимости от горного давления, наблюдаемое в сухих и водонасыщенных образцах известняка Bedford с порами в виде микротрещин. В течении замеров объем флюидов поддерживался постоянным. Здесь S = насыщенный, D = сухой, vP = скорость Р-волн, vS = скорость S-волн (Nur, 1981). | 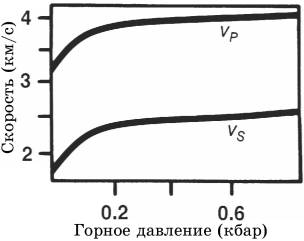 Рис.3.2 Изменение скоростей Р- и S-волн в зависимости от горного давления, наблюдаемое в образцах песчаника Berea с круглыми порами. В течение замеров объем флюидов поддерживался постоянным. Здесь vP = скорость Р-волн, vS = скорость S-волн (Nur, 1981). Рис.3.2 Изменение скоростей Р- и S-волн в зависимости от горного давления, наблюдаемое в образцах песчаника Berea с круглыми порами. В течение замеров объем флюидов поддерживался постоянным. Здесь vP = скорость Р-волн, vS = скорость S-волн (Nur, 1981). |
Между скоростью нормального приращения (скоростью ОГТ) и скоростью суммирования существует различие, которое на практике часто игнорируется. Скорость ОГТ основывается на гиперболичности времени пробега при коротких расстановках (Taner и Koehler, 1969; Al-Chalabi, 1973), а скорость суммирования исходит из гиперболы, которая наилучшим образом аппроксимирует данные по всей длине расстановки. Тем не менее, скорость суммирования и скорость ОГТ в общем случае рассматриваются как эквивалентные.
В основе общепринятого скоростного анализа находится предположение о гиперболичности годографа. В Разделе 3.3 рассмотрены различные подходы к скоростному анализу. Уравнение времени пробега является линейным в плоскости (t2, x2). Вертикальное время и скорость суммирования для данной ОП можно оценить по линии, которая наилучшим образом аппроксимирует точки времени пробега, построенные на плоскости (t2, x2) . Другой способ оценки скорости ОГТ – это применение различных поправок за нормальное приращение к выборке ОСТ с использованием диапазона постоянных скоростей с последующим отображением их в ряд. Скорость, которая наилучшим образом сглаживает каждое отражение в функции выноса, выбирается как его скорость ОГТ. С другой стороны, можно суммировать небольшой участок профиля, используя ряд постоянных скоростей. Затем эти суммы постоянных скоростей можно построить в виде панели, называемой панелью CVS. Скорости суммирования, которые дают желательную сумму, можно затем выбрать из панели.
Другая используемая обычно методика скоростного анализа основывается на расчете спектра скоростей. Идея состоит в отображении некоторой меры когерентности сигнала на графике зависимости от полного вертикального времени пробега. Принцип заключается в расчете когерентности сигнала на выборке ОСТ в малых временных окнах, которые следуют гиперболической траектории. Скорости суммирования интерпретируются по спектрам скоростей путем выбора скоростной функции, которая создает наибольшую когерентность на временах со значительными амплитудами отражений.
Необходимо определить изменение скорости суммирования по конкретной ОП. Скоростной анализ, ориентированный на горизонт, дает изменение скорости суммирования в латеральном направлении по горизонту, представляющему интерес. Рассмотрены практические аспекты этого метода, основанные на реальных данных.
В горизонтально-слоистой среде годограф отраженных волн не всегда являются гиперболическими. Одной из причин отклонения времени пробега от совершенной амплитуды является присутствие статических сдвигов, обусловленных приповерхностными изменениями скорости. Статика может сильно исказить гиперболу, если имеют место значительные изменения рельефа поверхности земли или при изменении 3мс в горизонтальном направлении. Остаточная статика часто сохраняется в данных даже после ввода начальных поправок за оцененные изменения 3мс и отметок превышения (т.е. за полевую статику – см. Раздел 3.6). Следовательно, перед суммированием необходимо рассчитать поправки за эту остаточную статику и применить к выборкам ОСТ. Оценка выполняется после предварительного ввода поправки за нормальное приращение с использованием региональной скоростной функции или информации, полученной из последовательности предварительных скоростных анализов по профилю. После коррекции остаточной статики скоростные анализы обычно повторяются с целью улучшения селекции волн по скорости для суммирования. различные аспекты коррекции остаточной статики рассмотрены в Разделах 3.4.и 3.5.
Наконец, скорости, требующиеся для процессов суммирования и миграции, - это не одно и то же. Для данных, собранных параллельно направлению падения одной ОП, скорость суммирования – это скорость в среде над ОП, деленная на косинус угла падения, а скорость миграции – это собственно скорость в среде. Другими словами, скорость суммирования чувствительна к углу падения, а скорость миграции нечувствительна. В Разделе 4.5 вводится теоретический метод определения скоростей миграции.
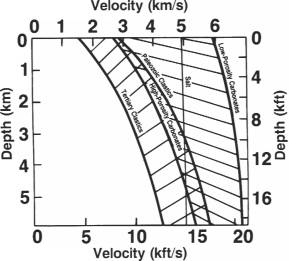 Рис.3.3 Пределы изменения скорости для пород различного состава на различных глубинах. (Sheriff, 1976; American Association of Petroleum Geologists). Рис.3.3 Пределы изменения скорости для пород различного состава на различных глубинах. (Sheriff, 1976; American Association of Petroleum Geologists). | 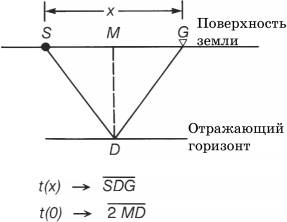 Рис.3.4 Геометрия нормального приращения для одной горизонтальной ОП [к уравнению (3.1)]. Рис.3.4 Геометрия нормального приращения для одной горизонтальной ОП [к уравнению (3.1)]. |
На рис.3.3: Tertiary Clastics – третичные обломочные породы; High-Porosity Carbonates – высоко пористые карбонаты; Paleozoic Clastics – палеозойские обломочные породы; Salt – соль; Low-Porosity Carbonates – низкопористые карбонаты.
НОРМАЛЬНОЕ ПРИРАЩЕНИЕ
На рис.3.4 показан простой случай одного горизонтального слоя. При данном положении средней точки М время пробега по лучу от положения ПВ S до глубинной точки D и к сейсмическому G равно t(x). Используя теорему Пифагора, запишем уравнение времени пробега в функции выноса:
| t2(x) = t2(0) + x2/v2 | (3.1) |
где x – расстояние между ПВ и сейсмоприемником; v – скорость в среде ОП; t(0) – полное время пробега по горизонтальному лучу MD. Вертикальная проекция глубинной точки D на поверхность по нормали к ОП совпадает со средней точкой М. Это справедливо только для горизонтальной ОП. Уравнение (3.1) описывает гиперболу в плоскости зависимости полного времени побега от выноса. Рис.3.5 – это пример трасс в выборке ОСТ (общих средних точек). Рисунок представляет также выборку ОГТ (общих глубинных точек), т.к. все лучи ассоциированные с каждой парой “взрыв-прибор”, отражаются от одной и той же глубинной точки D. На рис.3.5 вынос изменяется от 0 до 3150м с шагом между трассами 50м. Скорость в среде над ОП равна 2264м/с. Все трассы в этой выборке ОСТ содержат отражение от одной и той же глубинной точки. Разность между полным временем пробега при данном выносе t(x) и полным вертикальным временем пробега t(0) называется нормальным приращением. Из уравнения (3.1) видно, что скорость можно рассчитать, если известны вынос х и полное время пробега t(x) и t(0).
После того, как оценена скорость ОГТ, можно исправить времена пробега с целью устранения влияния выноса (рис.3.6). Затем трассы, исправленные за нормальное приращение, суммируются с целью получения суммарной трассы в положении данной ОСТ.
Процедура ввода поправки за гиперболическое нормальное приращение показана на рис.3.7. Идея состоит в нахождении величины амплитуды в точке А? на выборке, исправленной за нормальное приращение, по величине амплитуды в точке А на первоначальной выборке ОСТ. При данных t(0), x и vNMO рассчитаем t(x) по уравнению (3.1). Допустим, что оно равно 1003мс. Если шаг дискретизации был равен 4мс, это время соответствует индексу дискретизации (sample index), равному 250.25. Следовательно, необходимо рассчитать амплитуду при этом времени, используя амплитуды на соседних целочисленных выборках.
Поправка за нормальное приращение определяется разностью между t(x) и t(0):
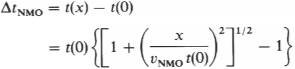 | (3.2) |
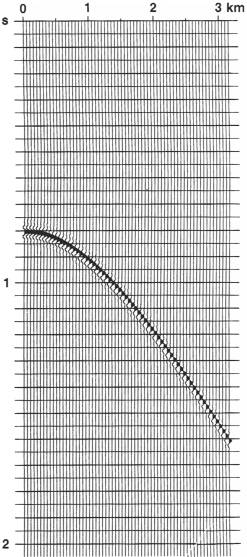 Рис.3.5 Синтетическая выборка ОСТ, ассоциированная с геометрией на рис.3.4. Кривая времени пробега для плоской ОП представляет собой гиперболу с вершиной, соответствующей вертикальному лучу. Таблица 3.1 Поправка за нормальное приращение в функции выноса х и полного вертикального времени для данной скоростной функции. Рис.3.5 Синтетическая выборка ОСТ, ассоциированная с геометрией на рис.3.4. Кривая времени пробега для плоской ОП представляет собой гиперболу с вершиной, соответствующей вертикальному лучу. Таблица 3.1 Поправка за нормальное приращение в функции выноса х и полного вертикального времени для данной скоростной функции. 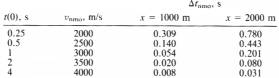 | 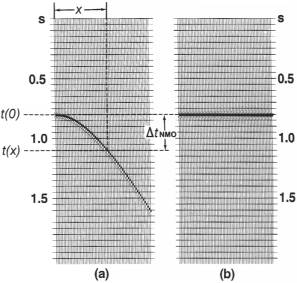 Рис.3.6 Поправка за нормальное приращение [уравнение (3.2)] включает определение положения времени пробега при ненулевом выносе t(x) на времени пробега при нулевом выносе t(0). (а) До поправки за нормальное приращение; (b) после поправки за нормальное приращение. Рис.3.6 Поправка за нормальное приращение [уравнение (3.2)] включает определение положения времени пробега при ненулевом выносе t(x) на времени пробега при нулевом выносе t(0). (а) До поправки за нормальное приращение; (b) после поправки за нормальное приращение. 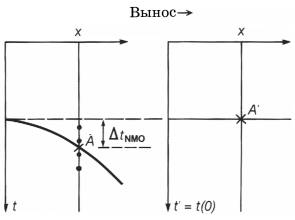 Рис.3.7 Ввод поправки за нормальное приращение с помощью компьютера. Для данных целой величины t(0), скорости и выноса расчета t(x), используется уравнение (3.1). Амплитуда при величине t(x), обозначенной А, необязательно попадает в положение входной целочисленной выборки. Используя по две выборки на обеих сторонах t(x) (обозначены точками), мы можем интерполировать между четырьмя значениями амплитуды, чтобы рассчитать амплитуду в t(x). Затем положение величины этой амплитуды определяется на целочисленной выборке t(0) (обозначена А?) при соответствующем выносе. Рис.3.7 Ввод поправки за нормальное приращение с помощью компьютера. Для данных целой величины t(0), скорости и выноса расчета t(x), используется уравнение (3.1). Амплитуда при величине t(x), обозначенной А, необязательно попадает в положение входной целочисленной выборки. Используя по две выборки на обеих сторонах t(x) (обозначены точками), мы можем интерполировать между четырьмя значениями амплитуды, чтобы рассчитать амплитуду в t(x). Затем положение величины этой амплитуды определяется на целочисленной выборке t(0) (обозначена А?) при соответствующем выносе. |
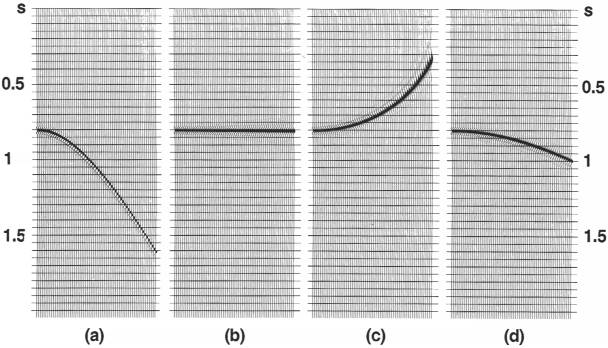 |
Рис.3.8 (а) Выборка ОСТ, содержащая одно отражение со скоростью нормального приращения 2264м/с; (b) выборка, исправленная за нормальное приращение с применением подходящей скорости приращения; (с) перекоррекция вследствие использования слишком низкой скорости (2000м/с); (d) недокоррекция из-за использования слишком высокой скорости (2500м/c).
В таблице 3.1 показаны поправки за нормальное приращение для двух различных величин; используется реалистичная скоростная функция, т.е. скорость возрастает с увеличением глубины ОП. Из этой таблицы можно видеть, что нормальное приращение возрастает с выносом и уменьшается с глубиной. Кроме того, нормальное приращение уменьшается при увеличении скорости.
Для плоской ОП, перекрываемой однородной средой, гиперболу отражения можно исправить за вынос, если в уравнении поправки за нормальное приращение используется правильная скорость в среде. На рис.3.8 видно, что если используется более высокая скорость, чем в действительности (2264м/с), гипербола сглаживается не полностью. Это называется недокоррекцией. С другой стороны, если используется более низкая скорость, происходит перекоррекция. На рис.3.8 показана основа общепринятого скоростного анализа. Поправка за нормальное приращение применяется к входным выборкам ОСТ с использованием ряда опытных постоянных скоростей в уравнении (3.2). Скорость, которая наилучшим образом сглаживает гиперболу отражения, - это скорость, которая наилучшим образом корректирует за нормальное приращение перед суммированием трасс в выборке. Более того, для простого случая одной горизонтальной ОП эта скорость также равна скорости в среде над ОП.
Нормальное приращение в горизонтально-слоистой среде
Рассмотрим среду, состоящую из горизонтальных слоев с равными скоростями (рис.3.9).Каждый слой имеет определенную мощность, которая может быть определена в единицах полного вертикального времени. Слои характеризуются интервальными скоростями (v1, v2, …, vN), где N – количество слоев. Рассмотрим траекторию от источника S до глубинной точки D и до сейсмоприемника R, ассоциированную с выносом х при положении средней точки М. Taner и Koehler (1969) вывели для этой траектории уравнение времени пробега:
| t2(x) = C0 + C1x2 + C2x4 + C3x6 + …, | (3.3) |
где C0 =t(0), C1 = 1/v2rms, C2, C3, … - сложные функции, которые зависят от мощности слоев и от интервальных скоростей. Среднеквадратичная скорость vrms до отражающей поверхности, на которой расположена глубинная точка D, определяется как:
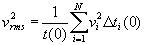 | (3.4) |
где Dti – вертикальное полное время пробега через i-тый слой, а, 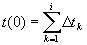 . Выполнив аппроксимацию короткой расстановкой (вынос мал по сравнению с глубиной), последовательность в уравнении (3.3) можно сократить:
. Выполнив аппроксимацию короткой расстановкой (вынос мал по сравнению с глубиной), последовательность в уравнении (3.3) можно сократить:
| t2(x) = t2(0) + x2/v2rms | (3.5) |
При сопоставлении уравнений (3.1) и (3.5) можно видеть, что скорость, требуемая для поправки за нормальное приращение в горизонтально-слоистой среде, равна среднеквадратичной скорости, при условии, что выполнена аппроксимация короткой расстановкой.
Насколько велика ошибка, вызываемая опусканием элементов более высокого порядка в уравнении (3.3)? На рис.3.10а показана выборка ОСТ, основанная на скоростной модели на рис.3.11. Времена пробега для всех четырех ОП были рассчитаны по интегральным уравнениям (Grant и West, 1965), которые точно описывают распространение волн в горизонтально-слоистой среде с данной моделью интервальных скоростей. Заменим слои, залегающие выше второго отражения при t(0) = 0.8с, одним слоем со скоростью, равной среднеквадратичной скорости до этой отражающей поверхности, т.е. 2264м/с. Полученная в результате кривая времени пробега, рассчитанная по уравнению (3.5), показана на рис.3.10b. Эта процедура повторяется для более глубоких отражений при t(0) = 1.2 и 1.6с на рис.3.10с и 3.10d. Обратите внимание, что кривые времени пробега на рис.3.10b, c и d представляют собой совершенные гиперболы. Насколько кривые времени пробега на рис.3.10а отличаются от этих гипербол? После тщательного исследования можно видеть, что времена пробега незначительно различаются для неглубоких отражений на временах t(0) = 0.8 и 1.2с только при больших выносов, в частности, более 3км. Опустив элементы более высокого порядка, мы аппроксимируем времена отражения в горизонтально-слоистой среде гиперболой короткой расстановки (small-spread hyperbola).
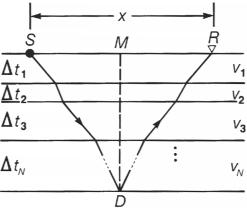 |
Рис.3.9 Нормальное приращение для горизонтально-слоистой модели разреза [геометрия для уравнения (3.3)].
