Расчёт ускоряющегося потока
Сила гидравлического удара прямо зависит от скорости, которую успел набрать останавливаемый поток. Достаточно определённо о скорости потока можно сказать только в одном случае — при резком перекрытии установившегося потока. Однако во многих случаях поток под воздействием внешнего давления (или, что то же самое, перепада уровней) периодически набирает некоторую скорость, после чего резко перекрывается, а затем цикл повторяется снова — таков, скажем, принцип работы гидравлических таранов. Этот же процесс имеет место при повторных циклах гидроудара независимо от того, был ли вызван первичный гидроудар перекрытием установившегося или ускорявшегося потока. Поэтому возникает необходимость определить следующие взаимосвязанные величины:
1. максимальную скорость, которую изначально покоящаяся жидкость под воздействием внешнего давления может набрать при заполнении трубы;
2. время, за которое на этом расстоянии поток наберёт заданную скорость (конечно, не превышающую максимально возможной);
3. скорость, которую поток может достичь, имея заданное расстояние для разгона.
При рассмотрении будем предполагать, что поток начинает заполнять горизонтальную пустую трубу, среда внутри которой не оказывает ему сколько-нибудь заметного сопротивления. Кроме того, давление в резервуаре на уровне входа в трубу также будем считать постоянным (это соответствует ситуации, когда объём резервуара намного больше заполняемого объёма трубы, либо такая неизменность давления обеспечивается специальными техническими средствами).
Расчёт сначала проведём без учёта потерь на гидравлическое трение (для сверхтекучей жидкости), а затем попробуем учесть потери.
Ускорение жидкости.
Прежде всего следует выяснить, где происходит ускорение жидкости — в трубе или вне её? Уравнение непрерывности даёт однозначный ответ: внутри трубы неизменного сечения скорость потока также неизменна, а следовательно, всё ускорение происходит в резервуаре перед трубой! В этом легко убедиться, наблюдая за сливом воды из ванны — «воронка» над сливным отверстием обусловлена именно зоной ускорения воды, находящейся в объёме самой ванны, а в сливной трубе скорость воды уже не меняется. Поэтому и энергия гидравлического удара обусловлена всем объёмом воды, двигающейся в трубе с одной и той же скоростью. \
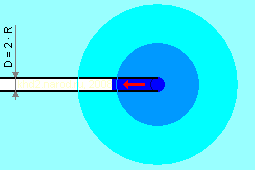
Вовлечение заполняющей трубу жидкости в движение вне трубы. Более насыщенным цветом показаны области с большей скоростью. Градации показаны условно, нарастание скорости происходит плавно.
Давайте определим форму границы области, на которой скорость жидкости меньше скорости в трубе на одну и ту же величину (форму эквискоростной поверхности). Поскольку вне трубы жидкость стремится к её входу со всех сторон в равной степени (давление-то везде одинаково), логично предположить, что при отсутствии каких-либо дополнительных направляющих граница этой области ускорения вокруг входа в трубу имеет сферическую форму. Впрочем, вблизи от входа трубы она будет несколько отличаться от сферической из-за того, что жидкость «сзади» от входа испытывает гидравлическое трение о стенки трубы и, к тому же, прежде чем попасть в внутрь, ей необходимо поменять направление, то есть ей труднее попасть в трубу, чем той, что находится напротив входа и практически не меняет направление движения вплоть до попадания внутрь трубы. Однако по мере удаления от входа влияние этих факторов ослабевает и форма эквискоростной поверхности будет всё более приближаться к сферической.
Следует отметить ещё один фактор, влияющий на форму эквискоростной поверхности — это градиент давления. Если он значителен (это имеет место возле поверхности, когда при относительно небольшом увеличении глубины давление может изменяться в разы), то такая поверхность приобретает яйцеобразную форму острым концом вверх, а уровню входа трубы соответствует самая широкая часть этого «яйца». На большой глубине, где на при той же разности уровней давление меняется лишь на малые доли процента, форма эквискоростной поверхности будет практически неотличима от идеальной сферы [4].
Остаётся определить закон, по которому меняется скорость жидкости во внешней среде по мере удаления от входа в трубу. Ответ определяется всё тем же уравнением непрерывности: скорость обратно пропорциональна площади сечения потока, а стало быть, квадрату расстояния от входа в трубу (при строгом расчёте из площади сферы необходимо вычесть площадь сегмента, соответствующего внешнему диаметру трубы, однако уже на расстоянии полутора радиусов от центра входа в трубу его доля составляет лишь немногим более 10%, в двух радиусах — около 7%, а в пяти радиусах — всего 1%).
