Волновой пакет и групповая скорость

Строго монохроматическая волна вида представляет собой бесконечную во времени и в пространстве последовательность «горбов» и «впадин», перемещающихся вдоль оси х с фазовой скоростью

(28-4)

Реальная волна всегда ограничена в пространстве и во времени и поэтому не является строго монохроматической.

Реальную волну, близкую к монохроматической, можно представить в виде суперпозиции (независимого наложения) большого числа волн – группы волн, мало отличающихся по частоте и занимающих ограниченную область в пространстве.

Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом (или группой волн).

При фиксированном времени t график функции, описывающей группу волн или волновой пакет, представлен на рис.28.3.

Для пакета имеет место соотношение . Чем меньше (диапазон частот, длин волн), тем больше и наоборот.

В недиспергирующей среде все волны, образующие пакет, распространяются с одинаковой фазовой скоростью 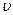. Очевидно, что в этом случае скорость движения пакета совпадает с фазовой, форма пакета со временем не изменяется. В диспергирующей среде (среде с дисперсией) волновой пакет расплывается, поскольку скорости его монохроматических составляющих отличаются друг от друга. Если дисперсия мала, расплывание волнового пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость U, под которой понимается скорость перемещения огибающей пакета, которую называют групповой скоростью.

На рис.28.4 показано положение волнового пакета для трех последовательных моментов времени и .

то это означает, что фазовая скорость данной группы волн превышает ее групповую скорость (как на рис.28.4).

Получим формулу для групповой скорости на примере волнового пакета из двух волн и несколько отличными друг от друга частотами. Пусть уравнение этих двух монохроматических волн имеют вид

В результате их сложение (наложение) образуется суммарная волна

.

Это выражение можно рассматривать как уравнение монохроматической волны, амплитуда которой меняется по закону

(28-5)

Нас будет интересовать скорость, с которой перемещается место с максимальной амплитудой – это и будет скорость волнового пакета – групповая скорость. Из выражения (28-5) следует, что точки, соответствующие, например, максимуму амплитуды (значение cos равно 1), движутся по закону

,

откуда Величина в скобках и есть групповая скорость

(28-6)

Связь фазовой и групповой скоростей (без вывода):

.

В отсутствии дисперсии и групповая скорость совпадает с фазовой.