Теорема о взаимности работ и взаимности перемещений

Рассмотрим два различных состояния (в порядке загружения) одной и той же упругой системы:состояния 1 при действии группы сил 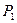и состояние 2 при действий группы сил 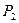на примере балки на рис.33, а. Определим и сопоставим работу внешних сил в следующих предположениях. Сначала система постепенно загружается силами состояния 1, а затем, когда силы достигнут окончательного значения, система будет постепенно нагружаться силами состояния 2.Во втором варианте последовательность приложения сил изменяется. Сначала система нагружается силами состояния 2, а затем -силами состояния 1.Допустим, что сперва на систему начала постепенно действовать нагрузка первого состояния , а потом- второго. Суммарная работа внешних сил будет выражаться алгебраической суммой .

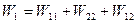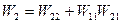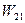Рассмотрим теперь приложение нагрузки в обратной последовательности, когда сначала прикладывается нагрузка второго, а затем – первого состояния. В этом случае суммарная работа внешних сил выразится следующей алгебраической суммой: , где -работа внешних сил второго состояния на перемещениях, вызванных действием сил первого состояния.

Согласно выражению (63), суммарная работа W внешних сил равна по абсолютной величине работе А внутренних сил, взятой с обратным знаком, или потенциальной энергии деформации U.

Известно, что в линейно деформируемой системе потенциальная энергия деформации не зависит от последовательности приложения внешних сил, а зависит только от исходного и конечного состояний системы. Поскольку исходное и конечное состояния системы в обоих случаях загружения одинаковы, то и суммарные работы внешних сил будут равны, т.е. 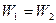или 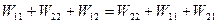, откуда

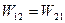(67)

Полученная аналитическая зависимость выражает собой теорему о взаимности работы и формируется так: в линейно деформируемом теле возможная работа внешних или внутренних сил первого состояния на перемещениях точек их приложения, вызванных действием сил второго состояния, равна возможной работе внешних или внутренних сил второго состояния перемещениях, вызванных действием сил первого состояния. Это так называемая теорема Бетти-Рэлея.

Теорема о взаимности перемещений может быть представлена как частный случай теоремы о взаимности работ. Пусть на балку в первом состоянии действует только одна единичная сила 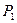, а во втором состоянии – тоже одна единичная сила 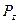(рис.34,а, б). Сила 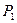приложена в точке 1, а сила 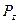– в точке 2. На основании теоремы о взаимности работ приравняем возможную работу внешних сил первого состояния на перемещениях второго состояния работе сил второго состояния на перемещениях первого состояния:

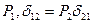или 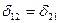. (68)

Это аналитическое выражение для теоремы взаимности перемещений, которая формулируется так: перемещение точки приложения первой единичной силы по направлению, вызванное действием второй единичной силы, равно перемещению по направлению второй единичной силы, вызванному действием первой единичной силы, это так называемая теорема Максвелла, имеющая фундаментальное значение в строительной механике.

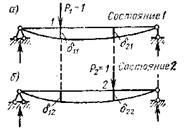
Рисунок 34 – Определение взаимности перемещений

Литература:

Основная: 6[разр.3: с 29-31; разр.5:с 36-47].

Контрольные вопросы:

1 Для чего нужно уменьшит размеры панелей и с какой целью вводятся дополнительные двухопорные фермочки-шпренгели, а также сколько и какие категории различают в шпренгельных фермах, и как определяются усилия в элементах основной и дополнительных ферм?

2 Какими функциями выражаются деформации (перемещения)в упругих системах и как аналитически это может быть записано, а также при каких допущениях, назовите их, перемещения, и деформации рассматриваемых упругих систем подчиняются закону независимости действия сил?

3 Для чего анализируют работу внешних и внутренних сил упругого тела и какими понятиями при этом пользуются в строительной механике, а также по какой зависимости определяется работа деформации элементов сооружения при статическом приложении внешних сил, дайте определение теореме Клайперона?

4 По какой зависимости определяется работа всех внешних сил действующих на балку и через какие силы может быть выражена работа внутренних сил упругой стержневой системы?

5 По какой зависимости определяется полная работа внутренних сил и почему работа внешних и внутренних сил называется возможной?

6 Какая аналитическая зависимость выражает теорему о взаимности работы и как формулируется (теорема Бетти-Релея)?