Тема лекции: Понятие о методе конечных элементов. Материалы металлических конструкций

В последнее время широкое распространение применительно к расчету инженерных конструкций (стержневых, листовых, оболочечных) получил метод конечных элементов МКЭ, базирующийся на рассмотрении конструкции в виде совокупности отдельных конструктивных элементов, соединенных в конечном числе узловых точек. Другими словами, расчетная схема исходной (стержневой) конструкции представляется совокупностью дискретных элементов (стержней). В узловых точках прикладываются некоторые фиктивные усилия взаимодействия, определяющие действие внутренних напряжений.

Каждому узловому перемещению (линейному или угловому) соответствует узловое усилие. Совокупность этих усилий определяет влияние смежных элементов (стержней) конструкции на рассматриваемый элемент.

Упругие свойства отдельных стержней, на которые разбиваются конструкции, определяются их матрицей податливости или матрицей жесткости. Эти матрицы определяют связь между узловыми усилиями и узловыми перемещениями рассматриваемого конечного элемента (стержня).

Матрица податливости рассматривается здесь для стержня постоянного поперечного сечения по длине. На рис. 57, а показан стержень, воспринимающий одно обобщенное усилие 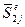, которому соответствует одно обобщенное перемещение 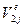, равное

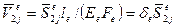, (109)

где δ_е – матрица коэффициентов податливости е-го стержня, воспринимающего только продольное усилие, δ_е = l_e/(E_eF_e) [1]; [1] – единичная матрица.

Для усилий и перемещений нижние первые значки указывают фиксированные направления силовых воздействий и перемещений, а вторые – номер узла. Так, например, 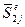- продольная сила на правом конце j элемента е.

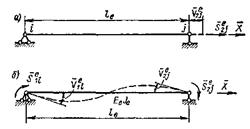
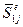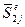Порядок матрицы податливости отдельного стержня (элемента) определяется числом независимых усилий, приложенных к нему. Так, на рис. 57, б показан е-й стержень, нагруженный по концам изгибающими моментами и . Направления моментов и де­формаций соответствуют положительным значениям. При учете только изгибных деформаций будем иметь матрицу податливости второго порядка. Углы поворота концевых сечений балки рав­няются:

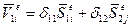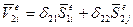; (110)

		Рисунок 58 – Деформированные состояния е-гостержня (метод перемещений) при осевом растяжении-сжатии (а)и изгибе (6)
	Рисунок 57 – Деформированные состояния е-го стержня (метод сил) при растяжении-сжатии (а) и изгибе (б)

что соответствует матричной форме

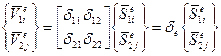. (111)

Углы поворота при действии единичных изгибающих моментов в опорных сечениях определяются по формуле Мора:

δ₁₁ = δ₂₂ = l_e/ (3E_eF_e); δ₁₂ = δ₂₂ = - l_e/ (6E_eF_e). (112)

Подставляя (112) в (111), получим

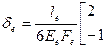
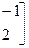– (113)

матрицу податливости прямолинейного стержня постоянного се­чения при изгибе. Матрицы податливости применяются в методе сил.

Матрица жесткости рассматривается здесь для одного е-гoэлемента (стержня) при осевом растяжении-сжатии (рис. 58, а).

Имеем два обобщенных усилия 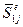, , 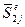которым соответствуют перемещения: 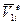- линейное перемещение левого конца вдоль оси стержня; 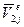- линейное перемещение правого конца вдоль оси стержня:

; ,

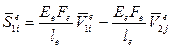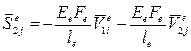или

,

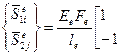
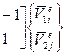где

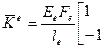
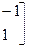– (114)

матрица жесткости е-гоэлемента при растяжении-сжатии.

Стержень, изображенный на рис. 58, а - совершенно сво­бодный, т. е. не закреплен в пространстве. Поэтому каждое узло­вое перемещение 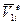, 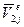зависит от неопределенных перемещений стержня как абсолютно твердого тела. Степень свободы стержня

По схеме рис. 58, а равняется единице. При этом матрица же­сткости 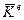стержня будет особенной. Ранг матрицы меньше ее порядка на число степеней свободы стержня как твердого тела. Для исключения перемещений стержня как абсолютно твердого тела следует ввести кинематическое закрепление. В данном слу­чае оно вводится в одном из узлов по направлению обобщенной узловой координаты 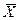. Исключение из матрицы 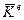– строки и столбца, соответствующих узловому перемещению, на которое наложена кинематическая связь, дает неособенную матрицу жесткости 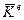. Полагая 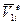= 0 или 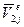= 0, получим

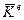= Е_е F_е [1] /l_е, (115)

где [1] – единичная матрица.

Из сопоставления матрицы податливости (ф-ла 106) и матрицы жесткости (112) для стержня, нагруженного продольной силой (рис. 57, а), имеем 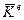= 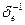, т. е. матрица жесткости обратная по отношению к матрице податливости.

Для стержня, нагруженного по концам изгибающими момен­тами и поперечными силами (рис. 58, 6), имеем четыре фиксированных силовых воздействия 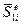, , 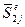, , 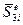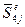которым соответствуют четыре перемещения 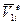, , 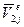, 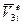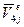. Используя по методу перемещений стандартные решения для балки, защемленной по концам, при единичных перемещениях узлов получим (табл. 2):

;

;

;

,

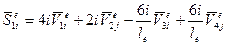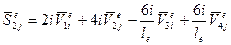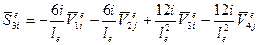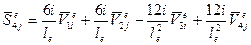или в матричном виде

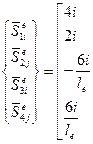
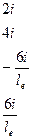
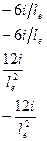
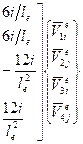; (116)

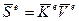, (117)

где 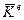– матрица жесткости матрица жесткости е-го элемента при изгибе; i = Е_еJ_e /l_e – линейная жесткость стержня. Выражение (117) является об­щим при любом виде деформированного состояния стержня.

Вводя кинематические закрепления в узлах по направлению узловой координаты 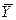, исключим перемещение стержня как абсолютно твердого тела. Это приводит к вычеркиванию третьих и четвертых строк и столбцов матрицы 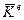, в результате чего и

получим неособенную урезанную матрицу

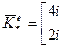
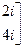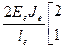
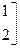= . (118)

Эта матрица (рис. 57, б) является обратной по отношению к матрице податливости (113).

При совместном учете деформаций изгиба и растяжения-сжатия стержня матрица жесткости 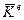определяется на основе двух матриц (114) и (116). Аналогично строятся матрицы жесткости для стержня при изгибе в двух плоскостях, а также при действии кручения. В общем случае матрица жесткости е-го элемента – всегда квадратная симметричная вида 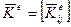, (119)

где i = 1, 2, …, n; j = 1, 2, …, n, в которой 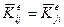при i ≠ j. Порядок п матрицы жесткости определяется количеством сил в узлах. Размерность членов матрицы (119) равняется единице.

Матрица преобразования координат Т используется для преобразования матриц жесткости 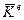стержневых элементов, полученных в собственных или местных системах координат 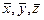, в матрицы жесткости К^е в общей системе координат х, у, z.

Компоненты узловых перемещений 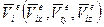е-го элемента и узловых усилий 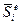преобразуются с помощью матриц преобразования координат:

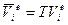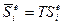; . (120)

В любой системе координат соответствующие компоненты сил совершают одну и ту же работу

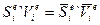, (121)

где ' – знак транспонирования.

Подставляя (120) в (121), получим

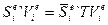, (122)

т.е. 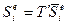. (123)

Используя (123) с учетом (117) и (120), получим

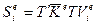, (124)

откуда 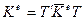, (125)

где К^е – матрица жесткости конечного элемента в общей системе координат х у z. Введем матрицу λ, составленную из косинусов углов между осями 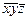и х у z:

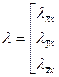
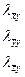
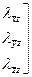, (126)

в которой значения направляющих косинусов ( 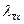, 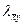и т.п.) определяются через координаты концов е-го стержня в общей системе координат.

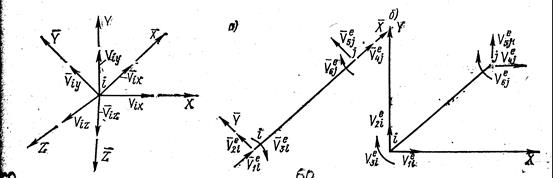
На рис. 59 показаны проекции линейного перемещения узла i на оси координат – местных и общих. Матрицы V_i и 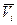состоят из трех компонентов:

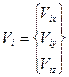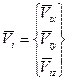; . (127)

Используя матрицу (126), получим

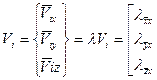
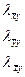
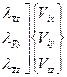. (128)

Для пространственных ферм матрица перемещений узла i е-го стержня в местной системе координат включает только 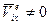, а 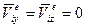, откуда

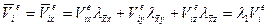, (129)

где 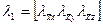. (130)

Для всего е-го стержня пространственной фермы имеем

,

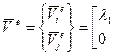
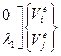где λ₁ определяется по выражению (130). Следовательно, матрица преобразования Т для элемента пространственной фермы имеет вид

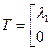
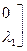. (131)

		Рисунок 60 – Стержень, работающий на изгиб с растяжением-сжатием в местной (а) и общей (б) системах координат
	Рисунок 59 – Составляющие перемещения узла I конструкции в 2-х системах координат: местной и общей

На рис. 60 показан элемент плоской рамы в общей и местной системах координат. Матрица преобразования Т узловых перемещений и узловых усилий из общей системы координат в местную имеет вид (126), в которой λ₁ в соответствии с выражением (131) содержит 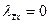, , 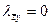, , 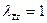, 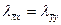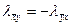т.е.

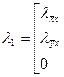
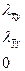
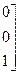, (132)

Матрица жесткости е-го элемента в общей системе координат х у z имеет вид

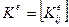, (133)

где i = 1, 2, …, n; j = 1, 2, …, n.

Матрица К^е определяется из выражения (125) и содержит члены, представляющие собой квадратные подматрицы размерности р – р, где р – число компонентов силы в рассматриваемых узлах.

Общая матрица жесткости конструкции формируется из матриц жесткости отдельных стержней. Построение ее осуществляется в общей системе координат х у z.

Рассмотрим общий случай воздействия внешней нагрузки Р в виде системы т сил в т узлах упругого тела. Матрицы нагрузки Р и перемещений V узловых точек по направлению сил имеют вид:

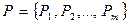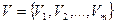; . (134)

Они связаны соотношением, аналогичным (117):

Р = КV, (135)

где К – матрица жесткости тела (конструкции).

Выражение (135) представим следующим образом:

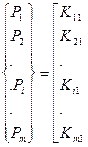
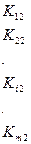
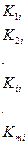
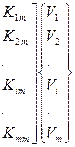. (136)

Из него следует выражение для силы Р_i, приложенной в i-м узле:

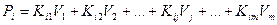. (137)

Каждая из внешних сил Р_і имеет столько же компонентов, сколько и узловые усилия 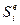(124) элементов рассматриваемой конструкции. Члены К_ij тоже представляют собой подматрицы, размерность которых определяется числом компонентов силы в соответствующем узле. Компоненты Р_і и 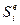направлены по координатным осям х, у, z. Каждый из компонентов Р_і равен сумме компонентов сил от всех стержней, соединяющихся в данном i-м узле:

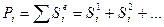, (138)

где 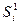, , 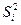… – силы, приложенные к узлу со стороны элементов 1 и 2 соответственно.

При этом только те стержни, которые содержат узел і, будут давать силы, отличные от нуля, хотя суммирование проводится по всем стержням. Учитывая выражение (117) в узле i

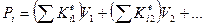. (139)

Из сопоставления (137) и (139) имеем, что член матрицы жесткости конструкции К_ij представляет собой сумму соответствующих членов матриц жесткости К_ij элементов, соединяющихся в узле i, т.е.

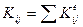. (140)

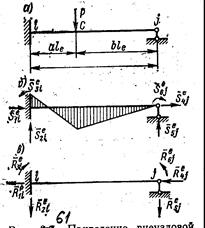
Рисунок 61 – Приведение внеузловой сосредоточенной нагрузки к узловой

Матрица нагрузки представляется в виде (131), где каждая из узловых сил Р_і в общей системе координат содержит столько же компонентов, сколько узловые силы элементов конструкции в той же системе кооринат. Последовательность записи этих компонентов аналогична последовательности для отдельных стержней. Так, например, для балочного элемента в плоской системе координат (рис. 60, б)

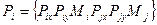. (141)

В общем случае (для балочных и рамных конструкций) на элементы действуют не только узловые, но и внеузловые нагрузки. В соответствии с выражениями (135) и (136) рассматривается равновесие узлов. Поэтому матрица Р узловой нагрузки должна содержать не только узловые внешние силы, приложенные непосредственно к узлам, но и эквивалентные им узловые усилия от действия внеузловой нагрузки. Внеузловая нагрузка вызывает появление реакций в виде сил и моментов в узлах.

Примем за положительные направления узловых реакций те же, что и для усилий на рис. 60, а. Рассмотрим в качестве примера стержневой е-й элемент в местных координатах для типичного случая внеузловой нагрузки (рис. 61).

На рис. 61, а показано действие внеузловой сосредоточенной силы Р. Матица узловых реакций при этом (рис. 61, б) равняется

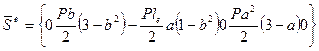, (142)

а матрица эквивалентных узловых усилий от действия силы Р, приведенных к узлам (рис. 61, в), будет

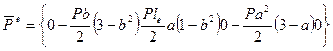. (143)

Для случаев приложения внеузловой сосредоточенной нагрузки (рис. 61, а) возможен и другой путь. В точке С приложения силы Р вводится новый узел, а е-й стержень разбивается на два: iC и Cj. Таким образом, сила оказывается приложенной в узле С в соответствии с общей идеей метода. Эквивалентные узловые силы 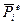в выражении (143) даны в местных координатах 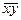е-го элемента. Вычислим матрицу этих сил в общей системе координат х у с помощью зависимости (123)

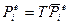. (144)

Теперь компоненты эквивалентных узловых сил элементов суммируются с соответствующими компонентами внешних сил в общих узлах рассматриваемой конструкции

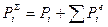. (145)

Суммирование в формуле (145) проводится по всем элементам, сходящимся в i-м узле.

Расчет стержневых конструкций по методу перемещений предусматривает составление в общей системе координат матричного произведения типа (117)

Р^∑ = КV, (146)

где К – общая матрица жесткости. Выражение (146) содержит уравнения равновесия (137) всех узлов конструкции. До сих пор система предполагалась совершенно свободной, в связи с чем каждое узловое перемещение V_i зависит от неопределенных значений перемещения конструкции как абсолютно твердого тела. При этом матрица жесткости конструкции К является особенной. Решение системы уравнений (146) возможно после того, как будут учтены граничные условия, т.е. в данном случае перемещения опор.

Введение определенного числа кинематических закреплений в отдельных узлах по направлениям опорных связей, т.е. V_n = 0, приводит к исключению из таблицы К соответствующих п-х строк и столбцов. Матрица К становится неособенной урезанной матрицей К^*. Уравнение равновесия (146) принимает вид

Р^* = К^*V^*. (147)

Однако такая операция – довольно трудоемкая и неудобная. Поэтому часто применяют искусственные приемы, которые позволяют сохранять общее число уравнений в системе неизменным. При этом преобразуются некоторые элементы матрицы К. Допустим, что имеется некоторая система т уравнений:

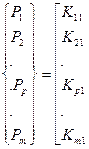
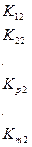
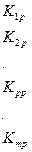
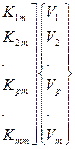. (148)

и, например, V_p = 0. В этом случае Р_р = 0, а остальные члены Р_і при i ≠ р остаются без изменения. Все члены р-й строки и р-го столбца будут нулевыми, а диагональный член К_рр=1. Матрица конструкции К, полученная после подобных преобразований из (148), называется преобразованной матрицей жесткости К^П.

После нахождения обратной матрицы К^{П – 1} определяем на основе уравнения (146) узловые перемещения конструкции в общей системе координат

V = К^{П – 1} Р^∑. (149)

Далее находим узловые перемещения 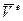е-го элемента в местной системе координат с помощью выражения (120) и узловые усилия 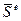по формуле (117). Для оценки прочности какого-либо стержневого элемента определяются компоненты напряжений 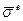. Расчет по МКЭ производится с помощью ЭВМ.