Пример выполнения контрольной работы. Внутри блоков структурной схемы записываем передаточные функции звеньев (рис.4)

Внутри блоков структурной схемы записываем передаточные функции звеньев (рис.4).

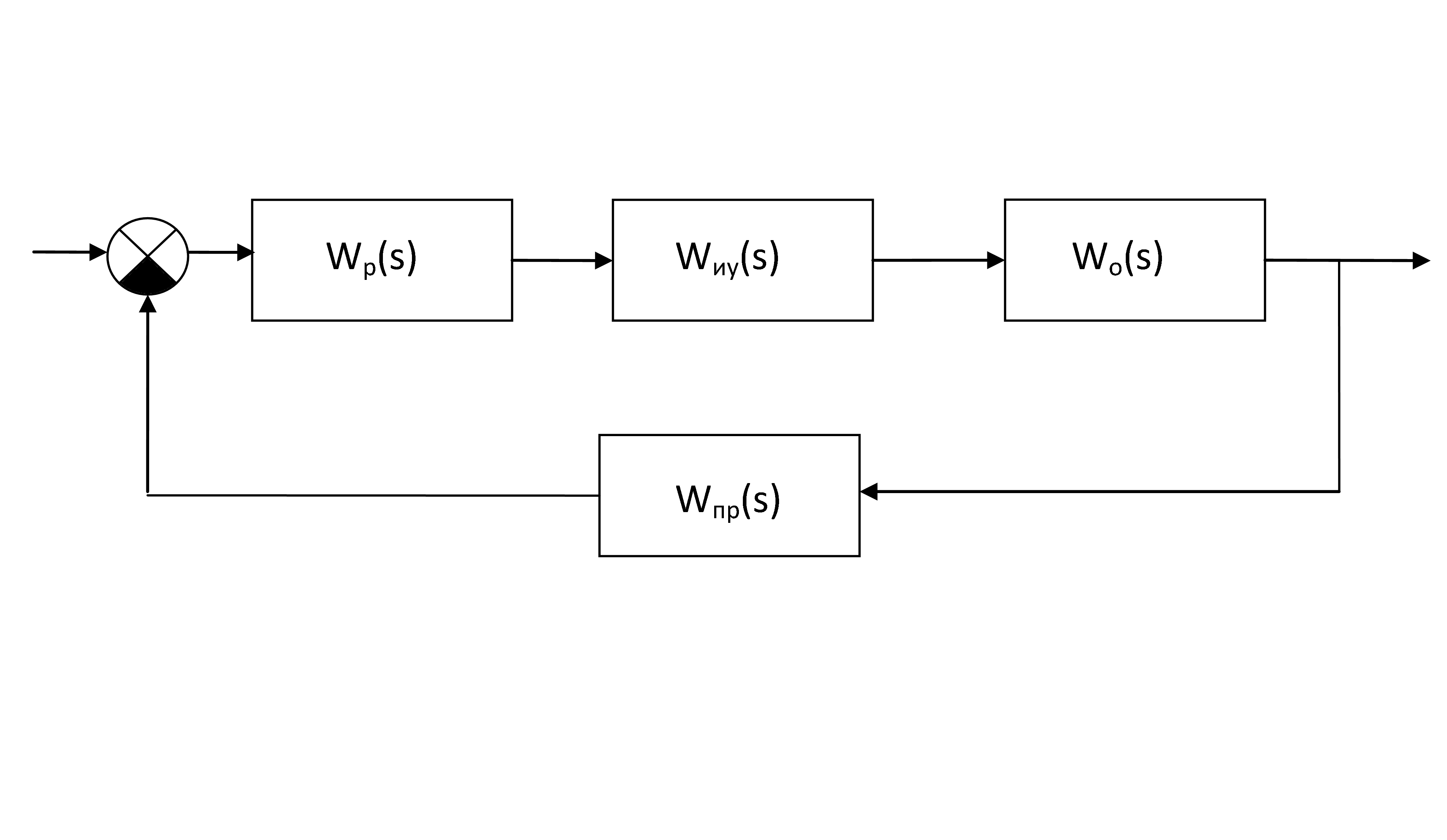
Рис. 4 Структурная схема САР расхода

Дано:

Т_о=3c; К_пр=0.6; К_иу=1; Т_иу=4с; К_п=2; Т_и=1с.

;

;

;

.

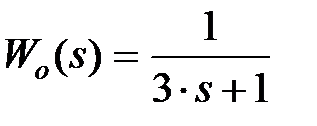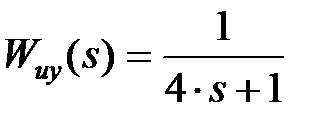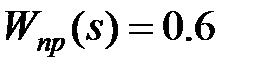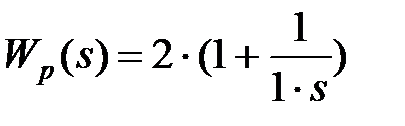Находим передаточную функцию разомкнутой системы, состоящую из последовательно соединенных звеньев: регулятора расхода, исполнительного устройства и объекта управления.

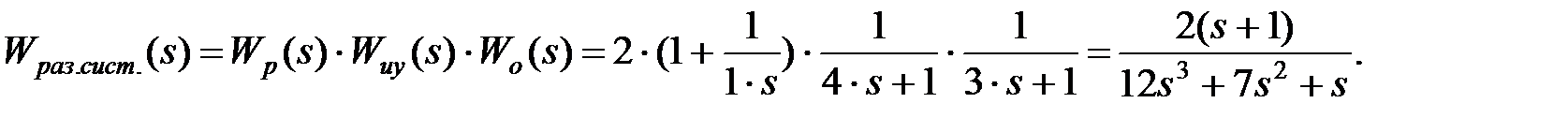
Находим передаточную функцию замкнутой системы:

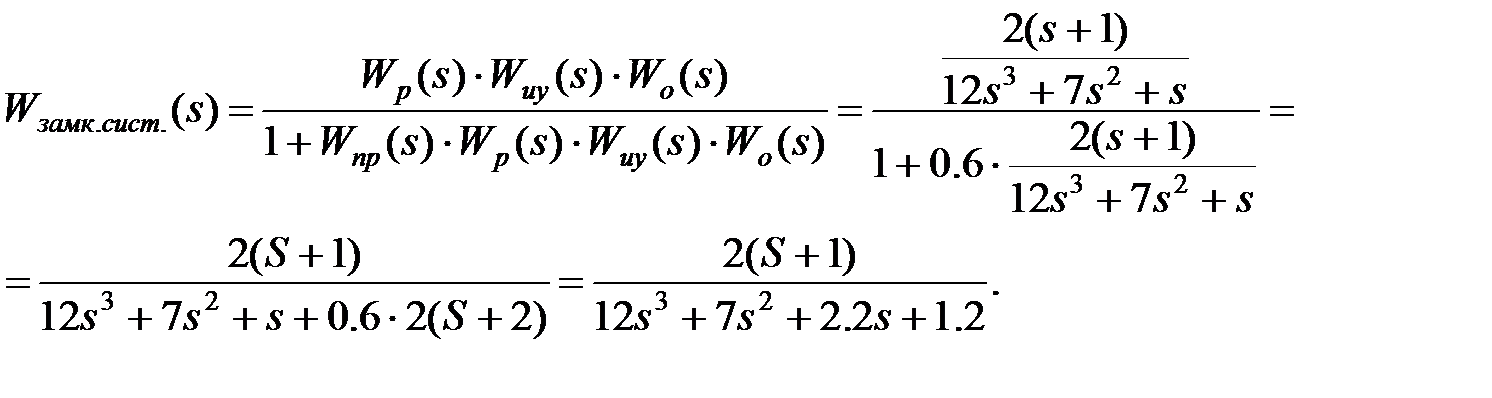
Знаменатель передаточной функции замкнутой системы называется характеристическим уравнением (полиномом). Выписываем его, приравниваем к нулю и анализируем.

.

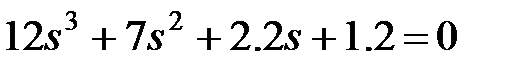Исследуем устойчивость САР по критерию Гурвица.

Характеристическое уравнение (полином) замкнутой системы имеет вид:

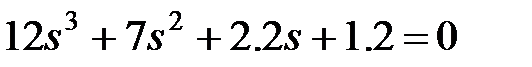
Составляем главный определитель Гурвица

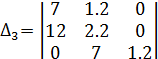
Определяем диагональные миноры этого определителя

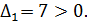
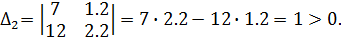
или

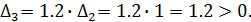
Все диагональные миноры главного определителя Гурвица ока­зались положительными, следовательно, все корни характеристи­ческого уравнения будут иметь отрицательные вещественные час­ти, а САР будет устойчива.

Определение устойчивости САР по критерию Михайлова.

Построить кривую-Михайлова и определить устойчивость сис­темы автоматического регулирования, если характеристическое уравнение имеет вид:

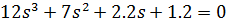
Решение.

Заменяем s на jw , в результате чего получим:

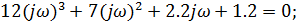
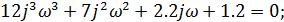
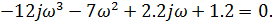
Выделим в характеристическом уравнении на вещественную и мнимую части:

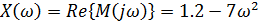
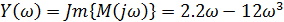
При w= 0 получим первую точку годографа Михайлова. Заносим значение в таблицу и отме­чаем координаты точки при w = 0 на комплексной плоскости:

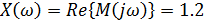
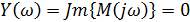
Определяем вторую точку пересечения годографа с осями ко­ординат. Значение частоты w, при которой характеристика пересекает мнимую ось, определяем, приравнивая вещественную часть к нулю:

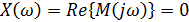
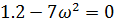
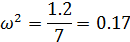
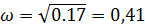
Находим значение мнимой части при этой частоте:

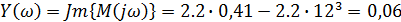
Заносим значение в табл. 2 и отме­чаем координаты точки при w = 0.41 на комплексной плоскости (рис. 5).

Находим третью точку пересечения кривой Михайлова с осями координат. Значение w, при котором годограф пересекает вещес­твенную ось между третьим и вторым квадрантами, находим, при­равнивая мнимую часть к нулю:

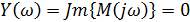
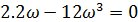
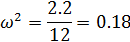
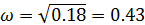
Находим значение вещественной части при этой частоте:

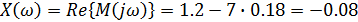
Находим значения мнимой и вещественной частей при значении

w = ¥ :

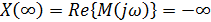
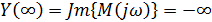
Результирующий угол поворота вектора при изменении w от 0 до ¥ равен 3p/2, поэтому система устойчива.

На рис. 5 пока­зана расчетная кривая Михайлова.

Таблица 2

ω		0,1	0,2	0,3	0,4	0,41	0,43	0,5	0,6	∞
X(ω)	1,2	1,13	0,92	0,57	0,08		-0,08	-0,55	-1,32	-∞
Y(ω)		0,21	0,34	0,34	0,11	0,06		-0,4	-1,27	-∞

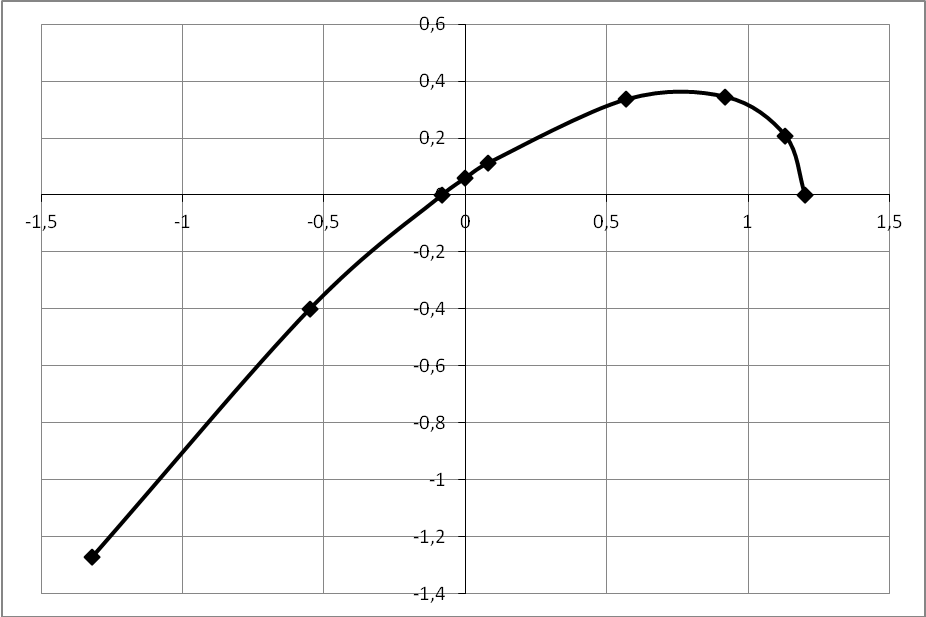
Рис. 5 Кривая Михайлова

X

jY