ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ. 1.Изучение способов построения линии пересечения двух поверхностей

ЦЕЛЬ РАБОТЫ

1.Изучение способов построения линии пересечения двух поверхностей.

2.Изучение методов определения натуральной величины фигуры сечения.

3.Изучение способов построения разверток поверхностей.

ОФОРМЛЕНИЕ РАБОТЫ

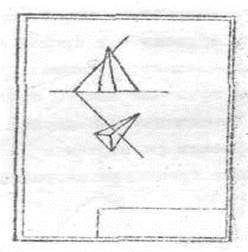На листе формата A3 в выбранном масштабе карандашом начертить заданный вариант, рис.1 (а, б). Основную надпись можно располагать вдоль длинной или короткой стороны формата. Все этапы решения выполнять на листе тонкими линиями. Обозначать точки, линии, следы плоскостей буквами или цифрами, стандартным шрифтом, при этом буквы и цифры располагать основанием параллельно основной надписи чертежа.

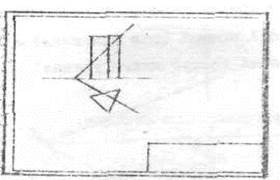а) в)

Рисунок 1

При решении задачи все дополнительные построения проводить тонкими линиями.

Все действия решений на плоскостях проекций обозначить буквами или цифрами независимо от положения элемента (следа плоскости, пря­мой и т.д.) буквы и цифры писать стандартным шрифтом номер 3 или 5 параллельно основной надписи.

После ответа на все поставленные в задании вопросы, работу проверяет преподаватель. 3атем работу обвести сучетом видимости, соответствующими линиями.

Секущую плоскость считать прозрачной.

СОДЕРЖАНИЕ ЗАДАНИЯ

1.Построить проекции фигуры сечения многогранника с данной плоскостью.

2.Определить истинную величину фигуры сечения.

3.Построить полную развертку усеченной части поверхности многогранника, указать линию сечения.

Перечень тем, изучение которых необходимо для выполнения данного задания:

1.Построение линии пересечения двух плоскостей.

2.Точки пересечения прямой с плоскостью.

3.Преобразование чертежа:

- метод вращения вокруг проецирующей прямой (оси вращения)

- ме­тод совмещения

- метод вращения вокруг линии уровня.

4.Построение развертки.

ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ

Первая часть задания:

1. Построениепроекции фигуры сечения.

Фигуру сечения многогранника плоскостью можно построить двумяспособами.

Первый способ: «способ граней», который заключается в построении линии пересечения каждой грани многогранника с заданной плоскостью. Этот способ применяется в том случае, если грани являются проецирующими плоскостями.

Пример. Дана трехгранная прямая призма и секущая плоскость Р. Плоскость Р занимает общее положение. Построить линию пересечения грани ВС с плоскостью Р (рис.2)

Рисунок 2

Каждая из граней призмы есть проецирующая плоскость.

1. Построить следы (Г₁ и Г₂) горизонтально-проецирующей плоскости Г грани ВС

2. Определяем линию пересечения MN плоскостей Г и Р и отмечаем отрезок прямой (1-2), по которому грань ВС пересеклась с плоскостью Р. ( 1₂ -2₂ ) фронтальная проекция.

3. Последовательно выполнив такое построение для каждой грани (АВ и АС) - определим фигуру сечения.

Второй способ: «способ ребер», который заключается в нахождении точек пересечения каждого ребра с данной плоскостью.

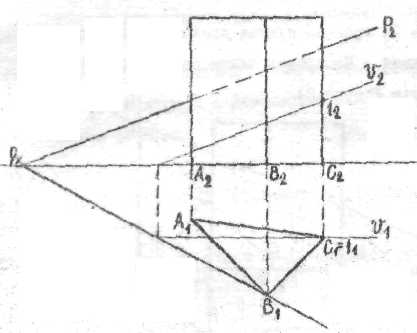Пример2. Дана трехгранная призма, все ребра которой горизонтально-проецирующие прямые, плоскость Р в пространстве занимает общее положение. Определить точку пересечения ребра С с плоскостью Р, рисунок З.

Рисунок 3

Ребро C является горизонтально - проецирующая прямая, следовательно горизонтальная проекция точки пересечения ребра С плоскостью Р, точка 1 совпадает с точкой С.

Фронтальную проекцию точки 1 определяем по принадлежности этой точкиплоскости Р для чего:

-через горизонтальную проекцию точки С (С1) проводим горизонтальную проекцию фронтали V1;

-фронтальная проекция этой фронтали в пересечении с фронтальной проекцией С2 ребра С определяет точку 12.

-выполняя аналогичные построения можно определить точки пересечения каждого ребра с плоскостью Р.

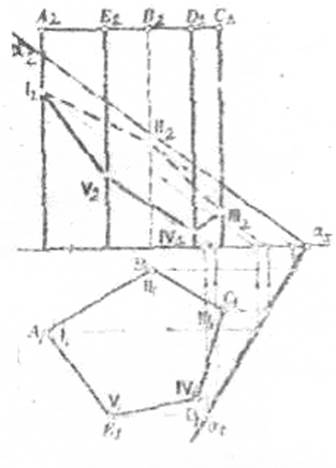-соединив последовательно полученные точки – определим фигуру сечения, рисунок 4.

Рисунок 4

В случае, когда многогранник – есть совокупность плоскостей и ребер общего положения, рисунок 4, задачу решают вторым способом, т.е. «способом ребер».

Задача построения фигуры сечения сводится к определению точки пересечения прямой (ребра) с плоскостью.

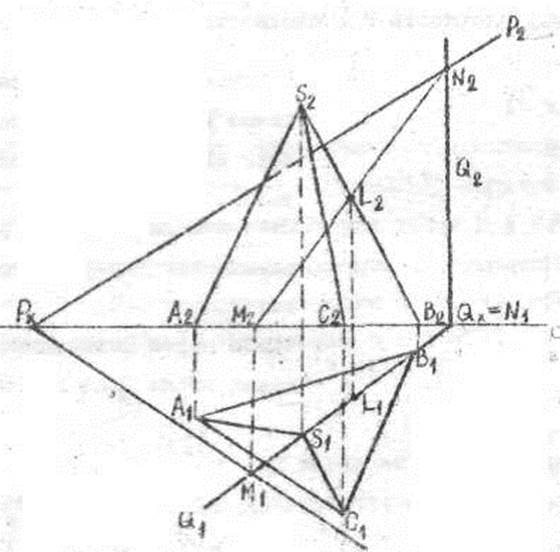Пример 3. Определить точку пересечения ребра SB с плоскостью Р, рисунок 4.

Рисунок 4

Выполняем следующие действия:

1.Через SBпроводим горизонтально-проецирующую плоскость Q, заданную следами Q₁, Q₂.

2.Находим прямую пересечения M1, N1; M2,N2 плоскостей Р ^ Q = MN.

3.Находим точку L(L1, L2) пересечения прямых SB ^ MN = L.

Аналогично находим точки пересечения ребер SA и SC с плоскостью Р.

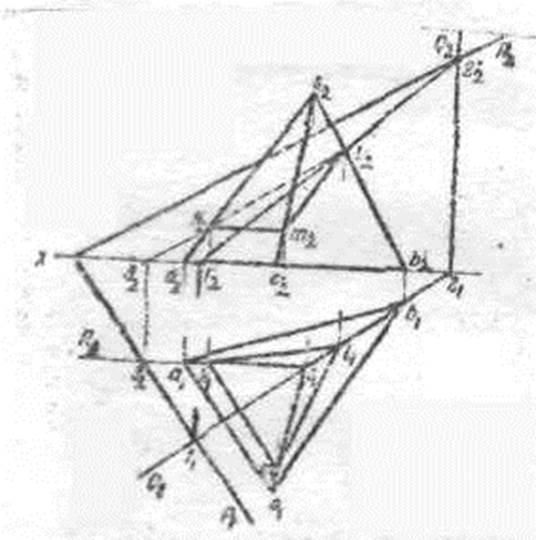Соединив последовательно точки сечения, получаем фигуру сечения, рисунок 5.

Рисунок 5

2.Определение натуральной величины фигуры сечения.

Так как фигуры сечения принадлежат плоскости сечения, то проще всего определить ее натуральную величину методом вращения плоскости сечения вокруг следа до совмещения с плоскостью проекций, в которой расположен этот след. Фигура сечения, расположенная в плоскости, изображается без искажения. Этот случай вращения называется «способом совмещения».

Пример 4. Совместить плоскость Р с плоскостью П₁ вращением вокруг сле­да P₁ , рисунок 6.

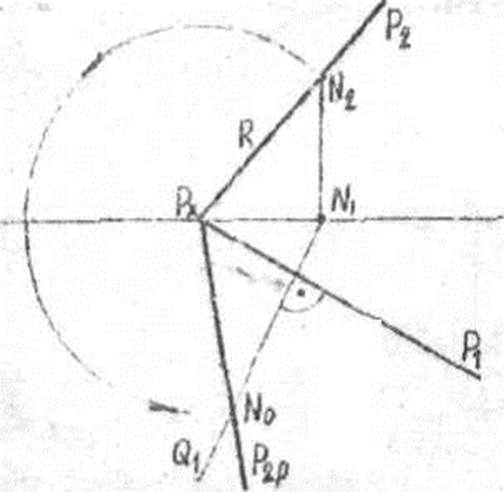Рисунок 6

Построение выполняем аналогично повороту плоскости вокруг ее горизонтальной или фронтальной линии уровня.

След плоскости можно рассматривать как «нулевую горизонталь».

Чтобы найти совмещенное положение следа Р₂ на плоскости П₁ необходимо:

1.Выбираем любую точку, например N (N₁ N₂) на следе Р₂.

2.При вращении плоскости Р вокруг следа Р1 точка N , будет вращаться в плос­кости Q P (Q₁ P₁). Отметим след плоскости вращения для точки N (Q₁).

3.Из Р_х, как из центра радиусом Р_х N₂ на следе Q₁ делаем засечку - получаем точку N₀.

4.Совмещенный след P2,0 пройдет через неподвижную точку Рх и N0.

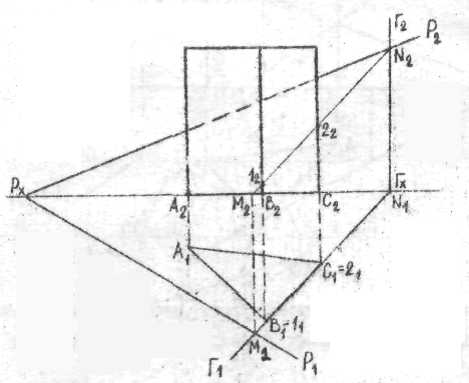
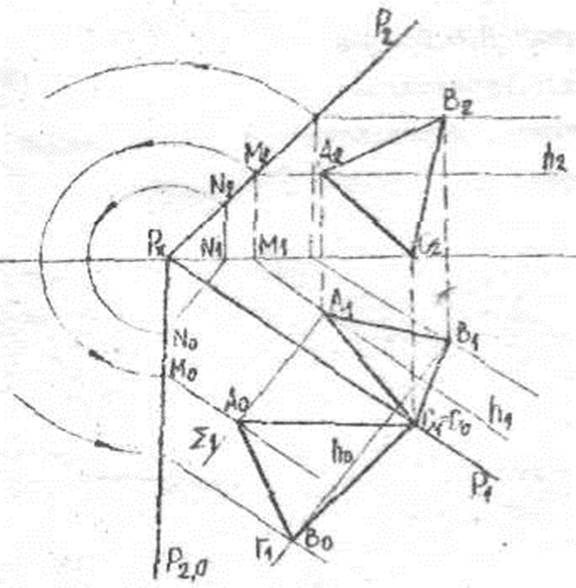
Пример 5. Определить истинную величину треугольника АВС расположенного в плоскости Р общего положения, рисунок 6. Точки А,В,С лежат на горизонталях плоскости Р.

1.Определяем положение совмещенного следа Р2,0. (см. пример 4).

2.Через точку А проводим след плоскости вращения Σ1 ┴ Р1 точка А? h.

3. Из Рх, как из центра радиусом Рх М2 отмечаем совмещенное положение следа горизонтали М0.

4. Через точку М₀ проводим совмещенную горизонталь h₀ //P1 до пересечения со следом плоскости вращения Σ1 – получим совмещенную точку А0.

Аналогично определяем положение точек В и С. Соединяем их между собой. А0В0С0 – натуральная величина треугольника.

Пример 6. Определить сечение четырехгранной призмы плоскостью, заданной параллельными прямыми а //б (Рис.7).

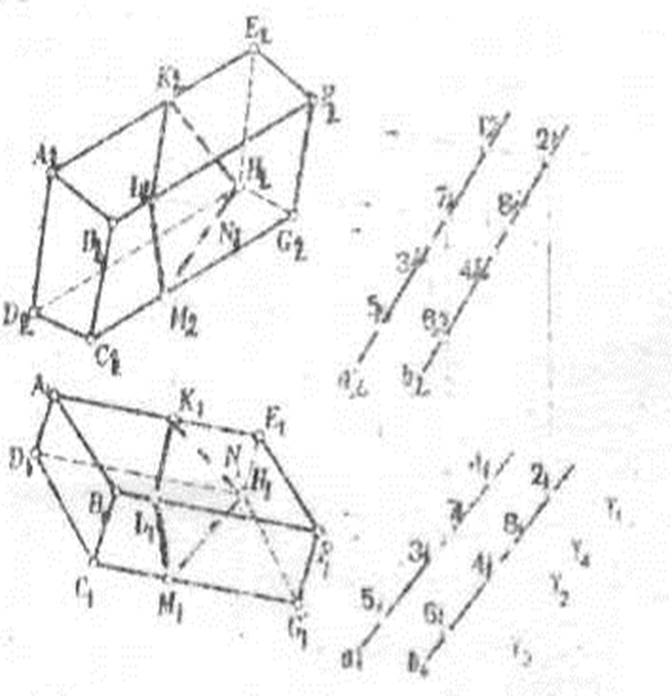Рисунок 7

СЕЧЕНИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ ПЛОСКОСТЬЮ.

I. Цель работы.

1. Изучение способов построения линии пересечения поверхности вращения и плоскости.

2. Изучение методов определения натуральной величины фигуры сечения.

3. Изучение способов построения развертки поверхностей вращения.