Понятие стохастической связи

В факторном анализе различают детерминированное и стохастическое моделирование.

С помощью детерминированных моделей исследуется функциональная связь между результативным показателем и факторами, т.е. когда одной величине факторного признака соответствует только одно значение результативного. Однако, не все экономические явления и процессы можно представить с помощью функциональных зависимостей. В этом случае моделируются и изучаются стохастические связи.

Под стохастикой понимается вероятность событий, обусловленных случайным сочетанием факторов. Стохастическая зависимость проявляется только в среднем в массе наблюдений, т.к. согласно закону больших чисел в большей совокупности закономерная связь выступает устойчивее случайного совпадения. При этом величине факторного признака может соответствовать несколько значений результативного показателя.

Например, в процессе анализа среднегодовую выработку рабочего можно представить в виде функциональной зависимости, выраженной произведением среднечасовой выработки, продолжительности рабочего дня и количества отработанных рабочим за год дней.

Однако, на выработку рабочего влияют и другие факторы, такие как условия труда, оплата труда, стаж, квалификация. Можно ли сразу представить связь выработки рабочего с этими факторами в виде формулы? Нет, т.к. такие зависимости проявляются в массе наблюдений, хотя совсем не обязательно это происходит в каждом конкретном случае.

Для изучения стохастических зависимостей используются различные способы и приемы:

- сравнение, аналитические группировки, графические и др., позволяющие установить общий характер и направленность связи и считающиеся простыми;

- способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа, позволяющие определить степень влияния факторов на изучаемый показатель и являющиеся более сложными.

Наиболее широкое распространение в группе последних нашел корреляционный анализ.

4.9 Корреляционный анализ и его значение для экономического анализа

Корреляция означает вероятностную зависимость между показателями, которая проявляется только в массе наблюдений. Например, известно, что рост квалификации ведет к росту производительности труда. Это положение подтверждается в большинстве случаев. Однако, это не означает, что у двух или трех рабочих одного разряда будет одинаковый уровень производительности труда.

Различают прямую и обратную корреляцию. Если направления изменений факторного и результативного признаков совпадают, то такая связь называется прямой, а если нет – то обратной.

Если исследуется наличие и теснота связи между двумя признаками, то корреляция называется парной, а если между тремя и более – множественной.

Тесноту связи характеризует коэффициент корреляции, который принимает значение от 0 до ±1. Если коэффициент корреляции близок к 1, то связь очень тесная, приближенная к детерминированной. Если он близок к 0, то это говорит об отсутствии связи между показателями.

Принято считать, что связь является:

- слабой, если коэффициент корреляции (по модулю) |r| находится в пределах 0< |r| 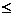0,3;

- умеренной, если коэффициент корреляции находится в пределах 0,3<|r| 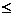0,75;

- тесной, если коэффициент корреляции находится в пределах 0,75<|r|<1.

Главной предпосылкой применения корреляционного анализа в анализе хозяйственной деятельности является возможность получения совокупности наблюдений одного и того же явления в различных условиях (либо по многим объектам, либо по одному объекту в динамике).

Значение корреляционного анализа для АХД состоит в расширении его возможностей и заключается:

– в определении количественной оценки стохастических связей и зависимостей;

– в углублении экономического анализа посредством дополнения детерминированного анализа корреляционным;

– в использовании его для обоснования планов, прогнозов, управленческих решений;

– в использовании его для количественной оценки внутрихозяйственных резервов.