Практическое занятие 10. Конверсия займов и формирование фонда погашения

Цель: Научиться составлять планы погашения по различным вариантам договора, а также рассчитывать параметры конверсионных займов.

Последовательность определения параметров конверсионного займа:

1. Определяется величина срочной уплаты по первоначальным условиям кредита по формуле:

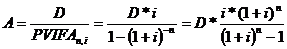
где A - размер срочной годовой уплаты до момента конверсии;

D - сумма предоставленного кредита в начале кредитной операции;

n - срок погашения задолженности по первоначальным условиям кредитного договора;

i - процентная ставка по первоначальным условиям кредитного договора.

1. Определяется остаток долга на момент конверсии, расчет производится по формуле:

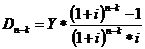
где k - число оплаченных расчетных периодов до момента изменения условий кредита.

3.Определяется величина срочной уплаты по новым условиям кредитного договора по формуле:

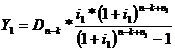
где Y1- размер срочной уплаты по новым условиям кредитного договора;

i1- процентная ставка по новым условиям кредитного договора;

n1- срок, на который продлевается период погашения задолженность по новым условиям кредитного договора.

Варианты создания погасительного фонда

1. проценты выплачиваются регулярно в конце каждого расчетного периода. Срочная уплата, включающая проценты и расходы по формированию фонда определяется:

Y=D*g+R = D*g+D/S_n,i ,

где D –размер предоставленного кредита;

g – ставка процента по кредиту;

R – взносы в фонд для погашения основного долга;

i – ставка процента по депозиту.

2. проценты присоединяются к сумме основного долга. Погашение кредита и начисление процентов производится в конце операции единовременной уплатой.

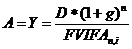
Расчет размера абсолютного грант-элемента:

W=D-G,

где W – абсолютный грант-элемент

D – сумма займа

G – современная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка.

Расчет относительного грант - элемента:

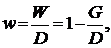где w –относительный грант - элемент.

При условии, что долг и проценты выплачиваются в виде постоянных срочных уплат формулы для определения абсолютного и относительного грант - элементов выглядят следующим образом:

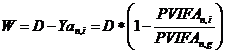
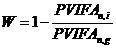
где PVIFA_n,i, PVIFA_n,g – коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентных ставок i и g, i>g.

Примеры решения задачи

Пример 10.1. Согласно кредитному соглашению, требуется оплатить кредит в сумме 900 тыс. грн. и начисленные на него проценты (10%) равными платежами в конце каждого года. Сумма ежегодного платежа - 200 тыс. грн.

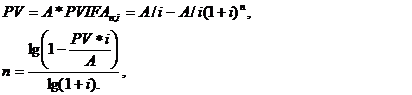Решение:

Срок такого кредитного соглашения определим по формуле обычной ренты:

В нашем случае РV = 900 тыс.грн., i==0,1 ; А = 200 тыс. грн.

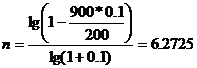План погашения кредита приведен в таблице 10.1.

Таблица 10.1 – План погашения кредита

Год	Остаток кредита (D)	Годовые взносы, млн
Срочные платежи (Y)	Проценты (I)	На погашение кредита (R)
			66,9	133,1
	535,9		53,59	146.41
	389,49		38,95	161,05
	228,44		22,84	177,16
	51,28	56,41	5,13	51,28

Ответ: общая сумма по погашению кредита без процентов: РV = 900 тыс. грн.; с процентами: FV= 1256,41 тыс. грн.

Пример 10.2 Для покупки автомобиля банк выделил денежную ссуду 25000 грн на 5 лет под 16 % годовых. Одноразовая комиссия составляет 1 %; первый взнос – 20% от цены автомобиля. Согласно условиям сделки, оплата ссуды и процентов происходит равными суммами. Составить план погашения задолжности, если уплаты осуществлялись в конце каждого года.

Решение:

Первый взнос =25000*20%=5000 грн.

Сумма кредита=20000 грн.

Банковская комиссия 20000*1%=200 грн

Ежегодный взнос определяется по формуле:

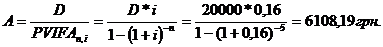
План погашения кредита приведен в таблице 10.2.

Таблица 10.2 – План погашения кредита

Год	Долг	Взнос	Гаш.%%	Гаш.долга
		6108,19		2908,19
	17091,81	6108,19	2734,69	3373,5
	13718,31	6108,19	2194,93	3913,26
	9805,049	6108,19	1568,80	4539,382
	5265,667	6108,19	842,50	5265,683

Задачи

1. Господин Иванов для покупки автомобиля берёт ссуду на 4 года в размере 17750 грн. под процентную ставку 15 %. Одноразовая комиссия банка составила 1 % от суммы кредита. Иванов в размере 15 % от цены автомобиля. Составить план погашения задолженности, если ссуду необходимо уплатить равными ежегодными срочными уплатами.

1. Кредит на недвижимость в сумме 100000 $, который необходимо погасить за 7 лет. За пользование кредитом ставка составляет 12 % годовых, первый взнос – 20 % от цены квартиры, одноразовая комиссия банка – 1 %. Составить план погашения, если сумма в счет погашения долга осуществляется равными ежегодными частями.

1. Выдан кредит на автомобиль в сумме 400 тыс. грн. под 13,5 % годовых на 3 года с погашением основного долга платежами, возрастающими ежегодно на 10 тыс. грн. Составить план погашения, если одноразовая банковская комиссия составляет 1 % от суммы кредита.

4. Долг в размере 100 000 грн. решено погасить по специальному графику за четыре года – размеры расходов по погашению долга по годам – 40000 грн., 20000 грн., 30000 грн. Остаток выплачивается в конце четвертого года. Ставка процентов по долгу установлена на уровне 10%. Составить план погашения.

1. Фермер приобрёл трактор в кредит за 120 000 грн. За кредит он должен платить 5% годовых и выплатить весь долг за 4 года. Найти размер ежегодной срочной уплаты и составить план погашения долга.

1. Господин Иванов купил в кредит автомобиль, который стоит 80 000 грн. Он обязался вернуть долг в течение года, делая равные ежемесячные срочные уплаты. Найти величину срочной уплаты и составить план погашения долга, если на долг магазин начисляет проценты по ставке а) i = 10% годовых, б) j₄ = 5% годовых.

7. Кредит, равный 8000 грн., под 35% должен погашаться равными срочными уплатами в течение 4-х лет. Составить план погашения задолженности, если срочные уплаты осуществляются :

a) в конце каждого года;

б) в конце каждого полугодия, при этом проценты начисляются 2 раза в год.

8. Кредит в 100000 грн. необходимо погасить за 4 года равными срочными уплатами. Проценты на долг начисляются по ставке 20% в год.

Составить план погашения задолженности для следующих вариантов:

а) уплаты в конце каждого года;

б) уплаты в конце каждого квартала, при этом проценты начисляются 4 раза в год;

в) уплаты в конце каждого месяца, при этом проценты начисляются 12 раз в год.

9. Долг в сумме 10000 грн. необходимо погасить последовательно равными суммами за 5 лет платежами постнумерандо. Составить план погашения задолженности, если за заем выплачиваются проценты по ставке 10% годовых.

10. Расходы по займу уменьшаются каждые год на 15%, общий срок погашения – 5 лет, первоначальная сумма долга – 15000 грн., ставка процента по долгу – 8%. Составить план погашения.

11. Иванов занимает 10 000 грн. при 6% годовых, проценты будет выплачивать в конце каждого года и создаст погасительный фонд для возмещения основной суммы через 10 лет. Какие необходимы годовые платежи, если фонд начисляет 4% годовых. Какую сумму будет содержать фонд в конце шестого года?

12. Найти относительный и абсолютный грант - элементы для беспроцентного займа, выданного на 5 лет в сумме 1000 грн., если рыночная ставка такого кредита 20%.

13. Кредит в размере 100 тыс. грн. выдан на 5 лет под номинальную ставку в 10% годовых с начислением процентов и погашением по полугодиям. Через 2 года от начала кредитования достигнуто соглашение о пролонгировании кредита на 2 года с переходом к годовому начислению процентов и ежегодному погашению долга с начислением процентов поставке 12 годовых. Составить план погашения задолженности .

14. В фонд погашения долга средства поступают в виде ежегодной ренты постнумерандо в течение 5 лет (срок погашения долга). Платежи каждый год увеличиваются на 500 000 грн. Размер долга на момент его погашения равен 10 млн.д.е., на взносы начисляются проценты по ставке 10% годовых. По условиям займа кредитору выплачивается 9,5% Разработать план создания фонда.

Практическое занятие 11. Погашение ипотечной ссуды

Цель:

Стандартная ипотека

Регулярный платеж по ипотечному кредиту для ренты постнумерандо:

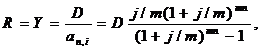где R – месячная сумма взносов;

D – сумма ссуды;

a_N;i – коэффициент приведения постоянной ренты;

N – общее число платежей, N = 12n (n – срок погашения в годах);

i – месячная ставка процента.

Регулярный платеж по ипотечному кредиту для ренты пренумерандо:

,

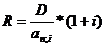Платеж, идущий на погашение ссуды рассчитывается по формуле:

,

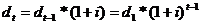где d_t – сумма погашения долга;

t – порядковый номер месяца;

i – месячная ставка процента.

Остаток долга на начало месяца:

D_t-1 = D_t–d_t; t = 1, …, 12n.,

Последовательные суммы погашения долга представляют собой геометрическую прогрессию с первым членом d₁ и знаменателем (1+i), причем:

d₁ = R – D*i.

Сумму членов этой прогрессии от начала погашения до t включительно найдем следующим образом:

W_t = d_1* FV_t;i ,

где FV_t;i – коэффициент наращения постоянной ренты постнумерандо.

Остаток долга на начало месяца находим как разность:

D_t+1 = D₁ – W_t .

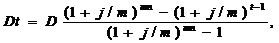или

Стандартная ипотека с неполным погашением задолженности и выплатой в конце срока остатка долга

Уравнение, балансирующее условия ипотеки, имеет вид:

D = Ra_n;;i + Bνⁿ ,

где В – остаток долга, который выплачивается в конце срока ипотечной ссуды;

νⁿ – множитель дисконтирования νⁿ = 1/(1+i)ⁿ.

Отсюда величина балансирующей выплаты в конце срока и срочной уплаты рассчитывается по формулам:

,

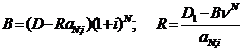Нестандартные ипотеки. Ипотека с ростом платежей.

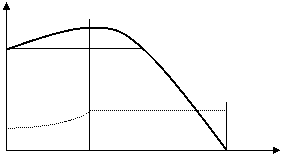
Особенность данной ипотеки заключается в следующем: первый взнос минимален, затем на некотором начальном интервале времени (пять-десять лет) они увеличиваются с постоянным темпом, далее они постоянны (см. рис.).

D

R

R₁

m M n

Рисунок – Схема погашения ипотеки с ростом платежей

Условные обозначения:

m – период роста срочных уплат;

М – период постоянных срочных уплат;

R – срочные уплаты;

D – сумма долга (величина ссуды)

n – срок ссуды.

Величина срочных уплат в первом периоде m рассчитывается следующим образом:

R_t = R₁ g^t-1 ,

где R₁ – расходы в первом месяце;

g – ежемесячный темп роста расходов.

Величина срочных уплат во втором периоде (расходы должника равны постоянной величине)

R = R₁ g^m-1 ,

Современная стоимость платежей первого периода:

.

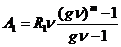Современная стоимость платежей второго периода:

/

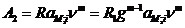Приравняем современную стоимость всего потока платежей к сумме задолженности, после чего, выполнив ряд преобразований, находим величину первой срочной уплаты:

.

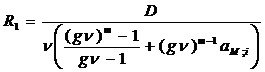
Ссуда с периодическим увеличением взносов

Совокупность выплаченных срочных уплат до момента k (при условии, что выплаты представляют собой ежегодную ренту с начислением процентов раз в год, ежегодную ренту с начислением процентов m – раз в год, р – срочную ренту с начислением процентов m – раз в год, причем m = р) определяется по формуле:

,

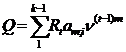где Q – современная стоимость взносов от первого до k – 1 периода включительно;

R_t – срочная уплата в момент времени t;

m – интервалы времени, через которые происходит увеличение взносов;

k – период, до которого происходила оплата взносов по ссуде.

Современная стоимость непокрытой взносами задолженности:

W = D – Q ,

где W – современная стоимость непокрытой взносами задолженности;

D – сумма долга.

Размер взносов в последнем периоде определяется как:

.

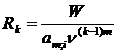Ссуда с залоговым счетом

Суммы списания с залогового счета определяются с использованием формулы:

V_t = V_t-1 q = V₁q^t-1,

где V_t – сумма, списываемая с залогового счета;

q — годовой темп изменения сумм, списываемых с залогового счета.

Современная стоимость суммы списаний с залогового счета:

,

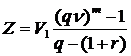где Z – сумма залогового счета;

r – месячная ставка процента, начисляемого на средства залогового счета;

V – дисконтный множитель по ставке г.

Отсюда сумма первого списания с залогового счета определяется как:

.

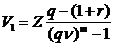В итоге сумма срочной уплаты рассчитывается по формуле:

R_t = R – V_t ; t=1, …, m.

где R – величина срочной уплаты.