В практическом смысле эффект от выбора того или иного способа зависит от значительности сумм, фигурирующих в финансовой операции.

Задачи

1. Предприятие взяло кредит 100000 грн. сроком на 2 года под 15% годовых и по истечении заемного периода должно вернуть кредит с процентами. Сколько должно заплатить предприятие? Проценты простые.

2. Молодая семья получила в банке ссуду на строительство жилья в размере 60 тыс. грн. сроком на 3 года под простую процентную ставку 21% годовых. Определите наращенную сумму кредита и сумму процентов.

3. Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 180 дней – 14%; при сроке 240 дней – 15; при сроке 270 дней –16%. Рассчитайте доход клиента при вкладе 10 тыс. грн. на указанные сроки. Год не високосный. Методика расчета: точные проценты с точным числом дней.

4. Клиент вложил в банк на депозит 2000$ на срок с 12 апреля по 26 июня с простой процентной ставкой 4% годовых. Рассчитайте доход клиента по трем методикам. Год не високосный.

5. Фирма внесла в коммерческий банк 28 тыс. грн. на срок с 9 ноября по 21 ноября того же года. На вклады «до востребования» банк начисляет проценты – 9% годовых. Проценты обыкновенные с приближенным числом дней в году. Определите наращенную сумму.

6. Коммерческий банк привлекает средства населения под простые проценты с процентной ставкой 17% годовых. Клиент внес 6 тыс. грн. на депозит с 12 февраля по 24 апреля. Определите величину коэффициента наращения и наращенную сумму для случая: а) точных процентов с точным числом дней; в) обыкновенных процентов с приближенным числом дней. Год не високосный.

7. Правекс – банк предлагает следующие условия для вкладов физических лиц: выплата процентов – ежемесячно, без права пополнения вклада, сумма вклада от 250 грн. проценты простые, методика расчеты точные проценты с точным числом дней. Необходимо рассчитать ежемесячную наращенную сумму и доход студента от полученной стипендии в размере 300 грн на срок 2 года.

Название вклада	Сумма вклада	1 мес	2 мес.	3 мес.	6 мес.	9 мес	12 мес. и 3 дн.	15 мес.	18 мес.	24 мес.
Правекс стандарт плюс	От 250 грн.	-	7,8	11,6	12,6	13,6	14,5	14,8		15,3

8. Клиент внес в банк 14 тыс. грн. на срок с 14 февраля по 23 июля. На вклады «до востребования» сроком больше месяца банк начисляет 7% годовых. Определите наращенную сумму при расчете по: а) точным процентам с точным числом дней; б) банковскому методу; в) обыкновенным процентам с приближенным числом дней. Год не високосный.

9. Коммерческий банк выдал ссуду в сумме 75 000 грн. под 15,5% простых годовых. По истечении срока кредита заемщик должен вернуть 85 000 грн. Определить срок, на который выдан кредит.

10. Банком был привлечен депозит 01.03.01 в сумме 3 500 грн. под 18% простых годовых. В конце срока депозита банк обязан выплатить клиенту 3850 грн. Определить срок депозита и дату его возврата.

11. На какой срок выдан кредит в 300 тыс. грн. под процентную ставку 25% годовых, если банк получил сумму от кредитора 380 тыс. грн. Методика расчета: обыкновенных % с приближенным числом дней.

12. Определите, какую процентную ставку должна установить при кредите 2000$ финансовая компания, чтобы при сроке кредита в 184 дня иметь прибыль не менее 120$. Проценты обыкновенные с приближенным числом дней.

13. Клиент получил кредит сроком на 9 месяцев в 6 тыс. грн. Сумма возврата кредита – 6,3 тыс. грн. Определите процентную ставку банка.

14. Коммерческий банк выдал кредит на период с 1.03 по 1.06 в сумме 150 000 грн. под 24% годовых при временной базе 360 дней и точным числом дней финансовой операции. Определить величину процентной ставки, обеспечивающей такой же процентный доход

а) при временной базе 365 дней;

б) при использовании приближенного количества дней финансовой операции.

15. Клиент поместил в банк 3 тыс. грн. 1 февраля. Процентная ставка банка с 1 февраля по 18 февраля – 7% годовых; с 19 февраля по 7 марта – 8% годовых; с 8 марта по 23 марта – 9% годовых; с 24 марта по 19 апреля, когда был изъят вклад - 10% годовых. Определите доход клиента и эффективную процентную ставку. Методика расчета: обыкновенные проценты с приближенным числом дней.

16. Клиент внес в сбербанк 3 тыс.грн. Согласно условиям договора «до востребования», процентная ставка может быть изменена банком в одностороннем порядке. Вклад внесен 3 апреля под 14% годовых. 22 апреля процентная ставка, согласно решению Правления банка, установлена в 15% годовых, а 20 мая – 13% годовых. Вклад вместе с процентами получен 3 июня. Определите наращенную сумму, если расчет процентов производится по точным процентам с точным числом дней в году (К=365).

17. Вкладчик заключил с банком депозитный договор на следующих условиях: сумма депозита 3 000 грн., срок 270 дней. Процентная ставка в первом квартале составляет 15%, во втором, третьем процентная ставка возрастает на 2,5%.Определить сумму полученную вкладчиком в конце срока депозита.

18. Коммерческий банк выдал кредит в размере 300 000 грн. на 3 года под 19% годовых. Через пол года процентная ставка была увеличена на 4,5%, еще через полгода заемщик погасил 150 000 основного долга, еще через год ставка была снижена до 21%. Определить сумму начисленных процентов и наращенную сумму.

Практическое занятие 3. Антисипативный метод начисления простых процентов

Цель: Изучить теоретические основы и получить практические навыки при расчетах по простым процентам антисипативным методом.

Антисипативный метод начисления предполагает, что проценты начисляются в начале временного интервала (удержание процента) исходя из наращенной суммы долга.

I = (FV-PV)*n=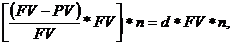

где 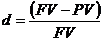по определению учётной ставки

Наращение по простой учетной ставке производится по формуле

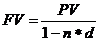(3.1)

где FV – будущая стоимость или наращенная сумма;

PV – первоначальная сумма(стоимость);

n – срок операции;

d – простая учетная ставка.

Если срок операции не целое число, то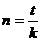

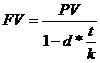
Дисконтирование – это расчетная операция обратная определению наращенной суммы, при которой определяется неизвестная первоначальная сумма PV, при известной наращиваемой сумме FV, при известном сроке финансовой операции и процентной ставке.

Операции дисконтирования необходимы при разработке условий финансовой сделки и при удержании процентов до наступления сроков погашения долга.

Существует 2 метода дисконтирования:

1 метод – Математическое дисконтирование:

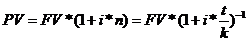
2 метод – Банковский учет

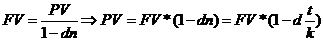
Другой весьма распространенной операцией краткосрочного характе­ра, для оценки которой используются рассмотренные формулы, является операция по учету векселей банком. В этом случае пользуются учетной ставкой. Схема действий в этом случае может быть следующей: владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т.е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называется дис­контом. В этом случае банк предлагает владельцу сумму (PV), исчисляе­мую исходя из объявленной банком учетной ставки (d). Очевид­но, что чем выше значение дисконтной ставки, тем большую сумму удер­живает банк в свою пользу. Расчет предоставляемой банком суммы ведет­ся по формуле, являющейся следствием формулы:

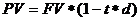
где t - относительная длина периода до погашения ссуды (отметим, что операция имеет смысл, когда число в скобках неотрицательно).

При учете векселя в банке до срока его погашения при сроке меньше года владелец векселя получит сумму, равную:

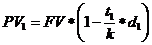
Наращенная сумма с учетом инфляции рассчитывается по формуле:

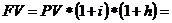
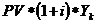
где h – темп инфляции;

Y_k – индекс инфляции за k-периодов (Y_k = (1+h₁)*(1+h₂)*…*(1+h_k)).

Вопросы для обсуждения:

- стоимость денег и время;

- сущность дисконтирования;

- виды дисконтирования;

- учет векселей;

- наращение по учетной ставке.

Пример решения задачи

ПримерКлиент оформляет вклад на срочный депозит сроком на 1 месяц в коммерческом банке. Процентная ставка банка 6 % годовых. Годовой уровень инфляции 4,8%. Определите реальную годовую процентную ставку прибыли, по которой оформлен вклад.

Решение:

Годовая процентная ставка с учетом инфляции рассчитывается по

формуле:

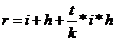
Отсюда реальная ставка доходности составит:

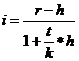
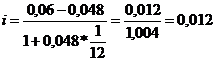
i = (0,06 – 0,048)/(1 + 1/12*0,048) = 0,18567.

Ответ: реальная ставка доходности по срочному депозиту составит 1,2% годовых.

Задачи

1. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть её через два года в размере 55000 грн. Банк определяет свой доход с использованием годовой учётной ставки 15 %.

2. Коммерческий банк выдал две ссуды 100 000 и 200 000 грн. под простой дисконт, равный 12% годовых и 13% годовых соответственно сроком на 2,5 года. Какую сумму банку необходимо выдать на руки одному и второму заемщику, какой доход получил банк?

1. Клиенту необходимо получить кредит в размере 388 000 грн. на 6 месяцев. Банк предоставляет кредит под простой дисконт 20% годовых. Определить сумму полученного кредита.

1. Предприятие намерено взять кредит в сумме 500 000 грн. Банк предоставляет кредит под:

а) 25 % простых годовых

б) простой дисконт 20 % годовых.

На какой срок фирма может взять кредит при условии, что подлежащая возврату сумма не должна превышать 900 000 грн.

5. Размер кредита, полученного фирмой на срок 6 месяцев, равен 600 тыс. грн. Сумма возврата кредита – 680 тыс. грн. Определите простую процентную и учетную ставку креди­та.

6. Предприятие для модернизации оборудования решило взять в банке кредит в 600 тыс. грн. на условиях, что проценты простые и оплачиваются при выдаче кредита. Кредит выдается под 20% го­довых. Срок кредита - 9 месяцев. Кроме того, банк требует 8% от суммы кредита в залог. Какую сумму получит заем­щик. Определите реальную процентную ставку для кре­дита.

7. Фирма получила на полгода банковский кредит в 800 тыс. грн. под 24% годовых. Проценты за кредит банк берет аван­сом. Рассчитайте реальную процентную ставку за кредит в случае: а) не требуется залога, б) залог за предоставление кредита составляет 6% от суммы кредита.

8. Фирма получила кредит на 3 месяца под залог недвижимо­сти стоимостью 16 тыс. грн. Величина кредита составляет 80% от стоимости недвижимости. Процентная ставка по кредиту - 36% годовых, комиссионные по обслуживанию кредита составляют 2%. Определите сумму полученного кредита, реальную процентную ставку и доход банка. Про­центы за кредит банк берет авансом.

1. Вексель номиналом 100 000 грн. выданный 1.06. на срок 3 месяца был учтен банком 20.06. по простой дисконтной ставке 20%. Определить сумму, полученную владельцем векселя.

1. Вексель номиналом 1 тыс.грн. выдан 1 сентября на 1 год. Ставка процентов по векселю составляет 18 % годовых. Какой доход получит банк в результате учета 25 декабря векселя, учетная ставка которого составляет 14%. Методика расчёта точные проценты.

1. Вексель номиналом 1 000 грн. сроком погашения через 180 дней был учтен банком за 45 дней до срока в сумме 925 грн. Определить учетную ставку банка.

1. Долговое обязательство в сумме 2 тыс. грн. должно быть погашено через 90 дней с процентами 16% простых годовых был предъявлен в коммерческий банк для учёта. Владелец обязательства учел его в банке в сумме 1,999 тыс. грн. по учетной ставке 16%. Определите период, за который банк учел вексель.

1. Банком был выдан кредит в размере 20000 тыс.грн. на 4 года под простую ставку 35% коммерческих годовых на условиях учета годового темпа инфляции. В первом году инфляция составила 5%, во втором - 7%, в третьем - 10%, в четвертом 15%. Определить сумму погашения.

1. Депозит в сумме 55 000 грн. сроком на 6 месяцев под 7,5% простых годовых был привлечен банком на условиях учета темпа инфляции. За период цены выросли в 1,5 раза. По истечении 6 месяцев вкладчик продлил депозитный договор еще на 3 месяца на тех же условиях. Ожидаемый темп инфляции на данный период составляет: 8 % в первом месяце, 9,5% - во втором, 11,5% - в третьем. Определить доход клиента.

ТЕМА 3. РАСЧЕТЫ ПО СЛОЖНЫМ ПОЦЕНТАМ

Практическое занятие 4. Декурсивный метод начисления сложных процентов

Цель: Изучить теоретические основы и получить практические навыки при расчетах по сложным процентам декурсивным методом.

Наращение	Дисконтирование
начисление %% 1 раз в году
FV = PV*(1 + i) n	PV= FV / (1+ i) n
начисление %% m раз в году (промежуточные проценты)
FV = PV*(1 + j/m) n*m	PV = FV / (1+ j/m) n*m

Для упрощения расчетов разработаны таблицы финансовых коэффициентов. Множитель (1 + i) ⁿ ( или (1 + j/m) ^n*m ) называется множителем наращения., обозначается FVIF_{i, n} или FVIF_{j/m, n*m} от англ. Future Value Interest Factor.(Приложение В) Множитель 1/(1 + i) ⁿ ( или 1/(1 + j/m) ^n*m ) называется множителем дисконтирования, или дисконт-фактор. Обозначается РVIF_{i, n} или РVIF_{j/m, n*m} от англ. Present Value Interest Factor.(Приложение Б)

Наращение	Дисконтирование
начисление %% 1 раз в году
FV = PV* FVIFi, n	PV= FV / FVIFi, n = FV* РVIFi, n
начисление %% m раз в году (промежуточные проценты)
FV = PV* FVIFj/m, n*m	PV = FV / FVIFj/m, n*m =FV* РVIFj/m, n*m

Таким образом, можно сделать несколько простых практических вы­водов:

• при начислении процентов: 12% годовых неэквивалентно 1% в месяц;
• чем чаще идет начисление по схеме сложных процентов, тем больше итоговая накопленная сумма.

Заметим, что для простых процентов такие выводы недействительны.

Начисление процентов за дробное число лет. Достаточно обыденными являются финансовые контракты, заключае­мые на период, отличающийся от целого числа лет. В этом случае про­центы могут начисляться одним из двух методов:

а) схема сложных процентов:

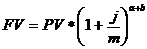
б) смешанная схема:

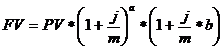
где а – целое число лет операции,

в – срок операции меньше года.

Непрерывное начисление процентов.

Все рассмотренные ранее начисляемые проценты называются дис­кретными, поскольку их начисление осуществляется за фиксированный промежуток времени (год, квартал, месяц, день, даже час). Уменьшая этот промежуток (период начисления) и увеличивая частоту начисления про­центов, в пределе можно перейти к так называемым непрерывным про­центам.

Формула наращения по непрерывной процентной ставке:

FV=PV*e^dn ,

где e – основание натурального логарифма е=2,718;

d - процентная ставка при начислении непрерывных процентов или сила роста;

e^dn - множителем наращения при непрерывной капитализации процентов.

Формула наращения с переменной силой роста:

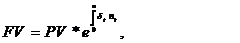Формула наращения для случая, если сила роста изменяется дискретно:

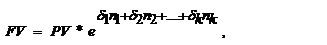где d₁,d₂,….d_к сила роста в соответствующих интервалах n₁,n₂,…n_к.

Формула наращения для случая, если сила роста изменяется непрерывно и может быть описана арифметической прогрессией:

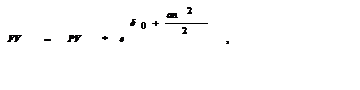где d₀- начальная величина силы роста;

a - годовой прирост или снижение силы роста.

Вопросы для обсуждения:

- начисление сложных процентов;

- понятие номинальной и эффективной ставки

- непрерывное начисление процентов;

- дисконтирование по сложным процентным ставкам;

- учет инфляции в финансовых операциях.

Примеры решения задач

Пример 4.1 Через два года фирме потребуются деньги в размере 30000 грн., какую сумму необходимо сегодня поместить в банк, начисляющий 15 % годовых, чтобы через 2 года получить требуемую сумму?

Решение:

Первоначальная сумма по известной будущей определяется по формуле:

PV= FV / (1+ i) ⁿ₌ 30000/(1+0,15)²=30000/1,3225=22684,4

Можно решить также с помощью таблиц множителей дисконтирования (Приложение Б)

PV= FV* РVIF_{i, n} =30000*0,7561=22683 (грн)

Или с помощью таблиц множителей наращения (Приложение В)

PV= FV / FVIF_{i, n} =30000/1,3225=22684,4 (грн)

Ответ: необходимо сейчас поместить в банк 22684, 4 грн., чтобы получить через 2 года 3000 грн.

Задачи

1. Клиент положил в банк 8000 грн. Какая сумма будет на счете этого клиента а)через 1 год, б)через 8 месяцев, в)через 4 года, г)через 6 лет 6 месяцев, если банк начисляет:

· 6% сложных годовых ;

· банк начисляет проценты по ставке j₃ = 6%.

1. Определите наращенную сумму вклада в 3 тыс. грн. при сроке вклада 2 года по номинальной процентной ставке 16 % годовых. Начисление процентов производится: а) один раз в год, б) по полугодиям, в) поквартально, г) ежемесячно.

3. Какие условия предпочтет клиент при получении кредита:

а) процентная ставка - 20%, начисление процентов ежемесячное;

б) процентная ставка - 22%, начисление процентов ежеквартальное;

в) процентная ставка - 23%, начисление процентов по полугодиям.

4. Для строительства завода банк предоставил фирме кредит в 200 тыс.$ сроком на 10 лет из расчета 13% годовых. Проведите расчет коэффициента наращения, суммы начисленных процентов и стоимости кредита на конец каждого года.

1. Банк выдал кредит в размере 75 000 грн. на 2 года и 170 дней под 25% сложных годовых. Определить, сумму к погашению и сумму начисленных процентов.

1. Банк принимает вклады от населения по номинальной процентной ставке 12% годовых. Начисление процентов ежемесячное. Вклад 1200$ был изъят через 102 дня. Определите доход клиента.

7. Бабушка хочет, чтобы на счете у внука через 18 лет была сумма 30 000 грн. Определить, какую сумму ей необходимо внести сейчас в банк, если на вклад начисляется 15% сложных годовых.

1. Г-н Иванов может вложить деньги в банк, выплачивающий проценты по ставке j₆= 10%. Какую сумму он должен вло­жить, чтобы получить 20 000 грн. через 3 года 3 месяца?

1. Г-н Петров хочет вложить 30 000грн., чтобы через 5 лет получить 40 000 грн. Под какую процентную ставку j₁₂ он должен вложить свои деньги?

1. Какой должна быть минимальная процентная ставка, чтобы произошло удвоение вклада за три года при начислении процентов: а) поквартально, б) ежемесячно.

1. ПроКредит банк (ProCredit bank) предлагает населению следующие условия для срочного депозита:

Вы вкладываете	Вы получаете
Сумма/ срок	90 дней	180 дней	367 дней	550 дней
5000 грн.	5138 грн.	5312 грн.	5696 грн.	6044 грн.

Определите ставку простых и сложных процентов при различных сроках начисления процентов.

1. Определите период времени, необходимый для удвоения капитала по простым и сложным процентам при процентной ставке 12% годовых. В последнем случае начисления процентов ежемесячное.

1. Ставка банка за пользование кредитом составляет 25%. Первые 2 года ставка процента не менялась. Каждые следующие 2 года ставка увеличивалась на 2%. Определите конечную сумму долга, если кредит в сумме 30 000 грн. был взят на 7 лет

1. По кредиту, полученному 5 лет назад фирма должна уплатить 250 000 грн. Процентная ставка по кредиту определена в 10,5% для 1-го года; для 2-го года ставка увеличивается на 1,5%; для 3-го и последующих лет ставка увеличивается на 0,75%. Определить сумму выданного кредита.

Практическое занятие 5. Антисипативный метод начисления сложных процентов.

Цель: Изучить теоретические основы и получить практические навыки при расчетах по сложным процентам антисипативным методом.

Наращение по сложной учетной ставке антисипативным методом производится по формуле

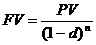
где FV – наращенная сумма;

PV –первоначальная сумма;

n – срок операции;

d –сложная учетная ставка.

Если капитализация процентов производится чаще, чем один раз в год, наращение по сложной учетной ставке производится по формуле

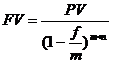
где f – номинальная учетная ставка;

m – число периодов капитализации в течение года.

Операции с векселями

При учете векселя в банке до срока его погашения владелец векселя получит сумму, равную:

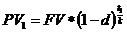
где t₁ – срок до момента погашения векселя;

При переучете векселя владелец векселя получит сумму:

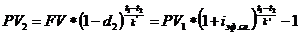
где k’ – количество дней в году согласно применяемой методике;

i_эф.сл. - эффективная процентная ставка сложных процентов для операции учета векселя.

Эффективная процентная ставка сложных процентов для операции учета векселя определяется по формуле:

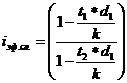-1

Начисление процентов и инфляция

Наращенная сумма по сложным процентам с учетом инфляции рассчитывается по формуле

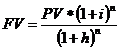
где h – темп инфляции.

Формула корректировки первоначальной суммы капитала на уровень инфляции

FV=PV*Y*(1+i)ⁿ,

где i – процентная ставка, отражающая реальную доходность финансовой операции;

Y – индекс инфляции.

Формула расчета процентной ставки, скорректированной на уровень инфляции (формула Фишера):

r=i+h+ih,

где r – процентная ставка, скорректированная на уровень инфляции;

i – процентная ставка, отражающая реальную доходность финансовой операции;

h – темп инфляции.

Начисление процентов и налоги

Простые проценты:

Проценты после уплаты налога:

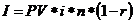
где r – ставка налога.

Наращенная сумма после уплаты налога:

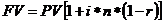
Сложные проценты:

Проценты после уплаты налога:

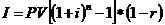
Наращенная сумма после уплаты налога:

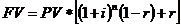
При начислении процентов m раз в году по номинальной процентной ставке j:

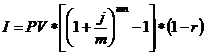
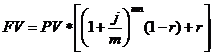
Вопросы для обсуждения:

- начисление сложных процентов антисипативным методом;

- дисконтирование по сложным учетным ставкам;

- операции по учету векселей.

Примеры решения задач

Пример 5.1. Получен кредит сроком на 2 года под 16% годовых. Проценты простые (сложные), и комиссионные составляют q = 1% от суммы кредита. Требуется определить эффективную процентную ставку доходности а) как ставку простых процентов, б) как ставку сложных процентов

Решение:

а) наращенная сумма кредита для кредитора:

FV = PV*(1 + i) ⁿ

Клиент получит сумму FV₁ = PV*(1 - q), и наращенная сумма кредита для клиента будет:

FV=PV*(1-q)*(1+ n*i_эф.пPV),

Отсюда:

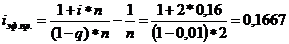
б) наращенная сумма кредита:

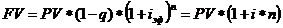
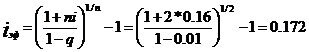в) если кредит получен под сложные проценты, то наращенная сумма кредита будет:

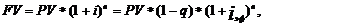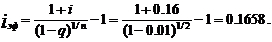Определим срок кредита и процентную ставку для случая сложных процентов.

Исходя из формулы 3.3 для срока ссуды п, имеем

Необходимая номинальная процентная ставка

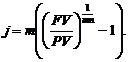Пример 5.2. Клиент внес в банк 1000$ на 2 года. Процентная ставка банка - 14%. Налог на проценты - 5%. Требуется определить сумму налога и наращенную сумму в случае: а) простых процентов, б) сложных процентов, в) сложных процентов при ежемесячном начислении.

Решение:

a) простые проценты:

Сумма налога рассчитывается по формуле:

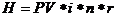
H₁= 1000*2 *0,14*0,05=14 $,

FV₁= 1000*[1 +2*0,14*(1-0,05)]= 1456$;

б) сложные проценты:

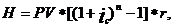Сумма налога рассчитывается по формуле:

Н₂ = 1000*[(1 + 0,14)² - 1 ]*0,05 = 14.98$,

FV₂ = 1000*[(1 + 0.14)² (1 - 0,05) + 0,05] = 1284,12 $;

в)сложные проценты при ежемесячном начислении:

Сумма налога рассчитывается по формуле:

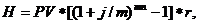H₃= 1000* [(1 +0,14/12)^12*2-1]*0,05=16,05$,

FV₃= 1000*[(1 +0,14/12)^12*2(1 -0,05)+0,05]= 1304,9$.

Пример 5.3. Месячные уровни инфляции 3%. Какой процент за годовой кредит должна взять финансовая компания, чтобы обеспечить доходность не менее 24%? Проценты сложные ч начисляются ежемесячно.

Преобразовав формулу 3.7, можно вывести формулу расчета наращенной суммы с учетом инфляции и начислении процентов по процентной ставке j:

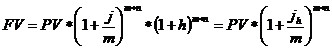
где j_h – номинальная процентная ставка, учитывающая уровень инфляции.

Отсюда

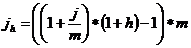
j_h= ((l +0,24/12 )(1 + 0,03)- l)l2= 0,6072

Ответ:J_h=60%

Задачи

1. Ссуда в размере 180 000 грн. была выдана на приобретение предприятием оборудования на 3 года и 4 месяца. Контрактом предусмотрено изменение ставки процента в зависимости от темпа инфляции. Базовая процентная ставка составляет 20% сложных годовых. Во втором году инфляция составила 12,5%, в третьем – 15%, в четвертом – 15,5%. Определить сумму погашающего платежа.

2. Коммерческий банк привлек депозит в сумме 17 000 грн. на 4 месяца под 25% годовых на условии корректировки депозитной ставки процента на инфляцию. За данный период цены выросли в 1,11 раза – в течение первого, второго, третьего месяцев, в четвертом месяце – на 9%. Определить:

а) ставку процента, учитывающую инфляцию;

б) наращенную сумму, полученную клиентом по истечении срока депозита;

в) сумму, которую реально получил вкладчик, если бы договором не предусматривалась корректировка депозитной ставки.

3. Коммерческий банк учел вексель за 110 дней до погашения по сложной учетной ставке 12% годовых. Вексель выдан в сумме 100 000 грн. на срок 6 месяцев. Определить сумму, которую банк заплатил в данной операции.

4. В результате учета векселя в сумме 150 000 грн., выданного на срок 3 года банк выплатил клиенту сумму 80 000 грн. Учетная ставка составила 32 % сложных годовых. Определить срок наступления платежа по векселю.

5. Определить номинальный учетный процент, по которому был учтен вексель номиналом 50000 грн. и сроком погашения 90 дней, если векселедержатель получил 48000 грн. Начисление процентов ежемесячное.

6. Владелец векселя учел его в банке за 3 месяца до срока погашения и получил 16000 грн. Номинальный учетный процент банка – 0,12. Проценты сложные и начисляются ежемесячно. Определить номинальную стоимость векселя.

7. Клиент вложил в банк 100 000 грн. Какая сумма будет на счете этого клиента через 1 год, если банк начисляет проценты по ставке а) j₃₆₀ = 5%, б) j¥=5%?

8. Какую сумму надо положить в банк, выплачивающий непрерывные проценты по ставке j_¥= 17%, чтобы через 10 лет на счете было 50 000 грн.

9. Банк начислял на вложенные в него деньги проценты непрерывно по ставке в первом году- 12%, во втором - 18%, в третьем и четвертом гг. - 24%. Какая сумма будет на счете 31 декабря четвертого года, если 1 января первого года на этот счёт было положено 30000 грн.?

10. Банк начисляет на вложенные в него деньги проценты по ставке j₄ = 16% и собирается перейти к непрерывному начислению процентов. Какую силу роста должен установить банк, чтобы доходы клиентов не изменились?

11. Клиент внес на депозит 4000 грн. сроком на 3 месяца под процентную ставку 12% годовых. Сумма, получения клиентом после окончания срока – 4400 грн. Определите процентную ставку налога на доход, если проценты начисляются:

а) простые;

б) сложные.

12. Определите доход клиента и налоговые деньги по срочному депозиту в 8 тыс. грн. на 6 месяцев с номинальной процентной ставкой 48% годовых, если процентная ставка налога 20%. Начисление процентов производится: а) поквартально, б) ежемесячно.

13. Три векселя номинальной стоимостью 30 тыс.грн. 50 и 80 тыс. грн. со сроками погашения 210, 240 и 270 дней объединяются в один номинальной стоимостью 180 тыс. грн. Объединение происходит по годовой ставке сложных процентов – 22 %. Найдите срок погашения объеденного процента.

ТЕМА 4. ЭКВИВАЛЕНТНОСТЬ ПРОЦЕНТНЫХ СТАВОК И ПЛАТЕЖЕЙ

Практическое занятие 6. Эквивалентность процентных ставок и платежей

Цель: Научиться составлять уравнения эквивалентности для определения ставок и параметров финансовых операций.

Современная стоимость денег – понятие относительное и зависит от выбранного современного момента времени.

В зависимости от выбранного современного момента времени современная ценность определяется с помощью операции дисконтирования или наращения, или не требует никаких математических операций.

В финансовой практике возникают ситуации, которые требуют изменения порядка начисления процентов. Для безубыточности операций определяются эквивалентные процентные ставки.

Эквивалентные процентные ставки – это ставки, которые обеспечивают равноценность финансовых последствий при различных вариантах осуществления операций.

Уравнение эквивалентности заключается в приравнивании соответствующего множителя наращения или дисконтирования для различных вариантов начисления процентов.

Ставка сложных процентов, эквивалентная ставке простых процентов рассчитывается по формуле

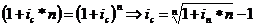
где i_n – простая процентная ставка

i_c – сложная процентная ставка

Уравнение эквивалентности основывается на равенстве платежей по первоначальным условиям, приведённым к некоторому моменту времени, платежам по новым условиям, приведённым к этому же моменту.

Два варианта изменения условий:

1.Совокупность платежей заменяется одним новым платежом

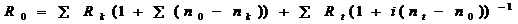Здесь возможно два варианта. При известном сроке объединённого платежа определяем сумму этого платежа. При расчётах по простым процентам уравнение эквивалентности будет следующего вида:

где R₀ – сумма объединенного платежа,

n_k, R_k – сумма платежей в соответствующие моменты времени, сроки выплат которых раньше срока R₀;

n_t, Rt – платежи и сроки этих платежей, если они осуществляются позже нового срока n₀.

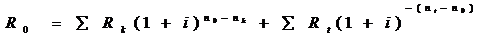При расчётах по сложным процентам уравнение эквивалентности имеет вид:

Для определения срока объединенного платежа по простым процентам составляется уравнение эквивалентности;

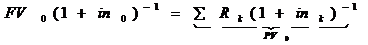где РV₀ – современная стоимость всех платежей по первоначальным условиям на нулевой момент времени.

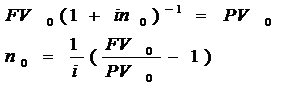Уравнение эквивалентности при расчётах по сложным процентам:

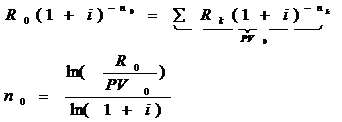Изменение условий контрактов может предусматривать изменение суммы и сроков платежей в любом согласованном порядке. Для определения параметров по новым условиям необходимо выбрать современный момент времени, которым может быть любая дата поступления денежных средств по новым, либо по старым вариантам и составить уравнение эквивалентности, к которому приравнять все платежи по новым условиям, приведённым к этому моменту времени, к платежам по первоначальным условиям, приведённым к этому же моменту времени.

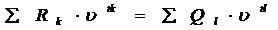Уравнение эквивалентности при расчётах по сложным процентам можно записать так:

где

R_k – платежи по первоначальным условиям в соответствующий момент времени, t_k

Q₁ – платежи по новым условиям в соответствующий момент времени, t₁

Вопросы для обсуждения:

- понятие современной ценности денег;

- понятие эквивалентности процентных ставок;

- изменение условий контрактов;

- расчет параметров операций при изменении условий контрактов;

- консолидация платежей.

Задачи

1. Коммерческий банк предлагает следующий простые депозитные ставки:

а) 15% при сроке вклада от 1 месяц;

б) 17% при сроке вклада 3 месяца;

в) 19% при сроке вклада 6 месяцев.

Рассчитать эквивалентную данным простым ставкам ставку сложных процентов.

1. Банк учитывает вексель за 60 дней до срока его оплаты по простой учётной ставке d_n= 6%. Какую сложную учётную ставку должен установить банк, чтобы доход банка не изме­нился?

1. Банк учитывает вексель

Наши рекомендации

Как видно, результат финансовой операции во многом зависит от выбора способа начисления простых процентов.

Выбор того или иного средства зависит от: цели рекламы, целевой аудитории, деятельности конкурентов, наличия денежных средств, специфики товара.

Зависит только от состояния системы и не зависит от того, каким путем это состояние достигнуто

Такому человеку нечего не нужно приобретать посредством того или иного действия; также ему нечего терять, если он воздерживается от действий. Он не зависит ни от кого и ни от чего.

Суть данного метода заключается в том, что при рассмотрении выбора применения того, или иного типа тепловой изоляции трубопроводов с положительными температурами, за основопола

Составить критерии выбора транспортных посредников для металлургического комбината. Составленным критериям выбора посредников присвоить веса в зависимости от значимости того или иного критерия.

Изучите возможные пути перехода от массовой рекламной стратегии к адресной, а также предполагаемые последствия выбора того или иного из них для организации вашей маркетинговой деятельности.

Использование того или иного типа дискуссии зависит от характера обсуждаемой проблемы и целей дискуссии.

Рубрикация. Выбор того или иного варианта нумерации зависит от содержания текста, его объема, состава, композиционной структуры

Тепловой эффект химической реакции зависит только от начального и конечного состояний веществ и не зависит от промежуточных стадий процесса

← Предыдущая страница | Следующая страница →