Вероятностные показатели оценки рисков

При использовании перечисленных выше методов предполагалось, что специалисты могут оценить количественные результаты рисковых событий и шансы их получения для определенного небольшого количества сценариев. Результаты такой оценки нетрудно свести в таблицу с указанием результата (дохода, NPV, доходности и т.п.) и его вероятности. Пусть, например, рассматривается возможность приобретения акций двух фирм «А» и «Б». Полученные экспертные оценки предполагаемых значений доходности по акциям и их вероятности представлены в табл. 3.5.

Таблица 3.6

Значения доходности по акциям, %, и их вероятности

Прогноз	Вероятность, р	Доходность акции
Фирма «А»	Фирма «Б»
Пессимистический	0,3	-70
Вероятный	0,4
Оптимистический	0,3

Очевидно, что можно построить множество различных сценариев развития событий. Однако полученная в итоге таблица результатов будет очень большой и непригодной для практического применения. Более удобный подход к описанию последствий рисковых событий заключается в задании некоторого правила, которое позволяет сопоставить каждому значению случайной величины вероятность его реализации. Такое правило называют законом распределения вероятностей случайной величины, а описывающую его математическую функцию – функцией распределения вероятностей.

Функцией распределения вероятностей F_x (x) случайной величины X называют функцию, ставящую в соответствие любому заданному значению х величину вероятности события {X < х}:

F_x (х) = р{Х < х},

где р - вероятность того, что значение случайной величины не превысит х.

Если F_x всюду непрерывна и дифференцируема, удобным способом описания случайной величины является функция плотности вероятности f_x(х), которая представляет собой производную функции распределения в точке х:

f_x(х) = F_x´(х).

Зная функцию распределения или плотности вероятностей случайной величины, можно делать выводы о степени достоверности соответствующих событий. На практике часто достаточно знать значения лишь нескольких характеристик, которые дают представление о распределении случайной величины. Важнейшими из них являются среднее значение (математическое ожидание), дисперсия и стандартное (среднее квадратичное) отклонение.

Среднее значение Е(Х) случайной величины X определяется как взвешенное из всех ее возможных значений с учетом вероятностей их реализации:

_i=n

Е(Х) = Σ x_ip_i,

ⁱ⁼¹

где p_i — вероятность реализации соответствующего значения х.

Вспомним, что интегральный эффект в методе сценариев и при построении дерева решений оценивался нами именно по формуле среднего значения.

Применим эту формулу для определения средней величины ожидаемой прибыли по акциям из примера:

R_А = 0,3 × (-70) + 0,4 × 15 + 0,3 × 100 = 15%.

R_Б = 0,3 × 10 + 0,4 × 15 + 0,3 × 20 = 15%.

Среднее значение случайной величины обычно играет важную роль в анализе, так как служит центром распределения ее вероятностей. Однако рассматриваемая изолированно от других показателей, эта характеристика не позволяет измерить степень риска проводимой операции.

Так, в приведенном примере средняя доходность по акциям обеих фирм одинакова и составляет 15%. Однако величины ожидаемых доходов в наиболее благоприятном случае, как и величины возможных убытков при неблагоприятном исходе будут существенно различаться.

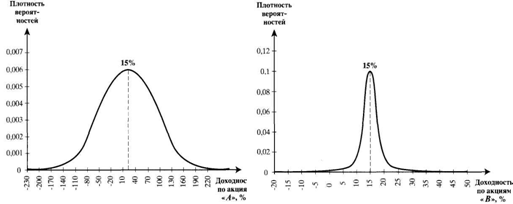
Рис 3.2. Графики плотности вероятности по акциям

Нетрудно заметить, что на графике (рис. 3.2) вероятностное распределение ожидаемого дохода по акциям фирмы «Б» сгруппировано вокруг среднего значения (15%) более плотно. Следовательно, вероятность того, что реальная доходность по этим акциям будет ниже средней, значительно меньше, чем по акциям фирмы «А». Таким образом, можно утверждать, что акции фирмы «Б» менее рисковые. Количественное обоснование этого утверждения может быть получено путем определения двух других характеристик распределения случайной величины — дисперсии и стандартного отклонения.

Дисперсия D и стандартное отклонение σ служат характеристиками разброса (вариации) случайной величины от ее центра распределения (среднего значения).

Дисперсия определяется как сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на их вероятности:

_i=n

D(Х) = Σ p_i(x_i, - Е(Х))².

ⁱ⁼¹

Рассчитаем дисперсии доходности по акциям фирм «А» и «В» из примера. Они соответственно будут равны:

D(R_A) = 0,3(100 - 15)² + 0,4(15 - 15)² +0,3(-70 - 15)² = 4335.

D(R_B) = 0,3(200 - 15)² +0,4(15 - 15)² + 0,3(10 - 15)² = 15.

Проведенные расчеты дают количественное подтверждение результатов графического анализа. Разброс доходности относительно среднего значения, а следовательно, и риск по акциям фирмы «Б» значительно меньше, чем по акциям фирмы «А».

Несмотря на то, что дисперсия служит мерой риска, использовать ее на практике неудобно. Размерность дисперсии равна квадрату единицы измерения случайной величины. Очевидно, что на практике невозможно при оценке рисков использовать «рубль²» или «%²». Результаты анализа более наглядны, если разброс случайной величины выражен в тех же единицах измерения, что и сама случайная величина, т.е. в рублях или в процентах. Для того чтобы достигнуть этой цели, в качестве меры разброса случайной величины используют другой показатель — стандартное (среднее квадратичное) отклонение, рассчитываемое по формуле

σ_X = √ D(Х).

Таким образом, величина σ_X представляет собой средневзвешенное отклонение случайной величины от ее математического ожидания, а в качестве весов берутся соответствующие вероятности. Выраженное в тех же единицах, стандартное отклонение показывает, насколько значения случайной величины могут отличаться от ее среднего. Чем меньше стандартное отклонение, тем уже диапазон вероятностного распределения и тем ниже риск, связанный с данной операцией. При анализе рисков стандартное отклонение часто называют главной мерой риска или даже просто риском.

Рассчитаем стандартные отклонения доходности акций для рассматриваемого примера:

σ_А = √D(А) = √4335 = 65,84. σ_Б = √D(Б) = √15 = 3,87.

Полученные результаты показывают, что диапазон колебаний доходности по акциям фирмы «А» в пределах одного среднеквадратичного отклонения от ожидаемого значения составляет от -50,84% до 80,84% (15 ± 65,84), тогда как для фирмы «Б» он значительно уже: от 11,13% до 18,87% (15 ± 3,87).

Приведенные графики были построены, исходя из предположения, что доходность по акциям фирм подчиняется закону нормального распределения вероятностей. Этот закон широко используется в теории финансового менеджмента при оценке рисков. Характеристики нормального распределения:

1) требует знания всего двух параметров — среднего значения и дисперсии случайной величины;

2) график кривой плотности нормального распределения симметричен и имеет форму колокола, центр которого приходится на среднее значение Е(Х);

3) максимум функции плотности вероятностей соответствует точке Е(Х) = а и равен величине 1/√ 2πσ;

4) «размах» (сжатие или растяжение графика) определяется дисперсией или стандартным отклонением σ. Чем больше показатель σ, тем больше «разброс», тем выше вероятность того, что случайная величина будет отличаться от среднего ожидаемого значения;

5) площадь, ограниченная кривой функции плотности, равна 1;

6) вероятность больших отклонений нормально распределенной случайной величины Х от ее среднего значения Е(Х) ничтожно мала;

7) нормальная случайная величина Х с математическим ожиданием Е(Х) и стандартным отклонением σ_X с вероятностью, близкой к 1, попадает в интервал: Е(Х) - 3σ < Е(Х) < Е(Х) + 3σ. Это соотношение известно как правило «трех сигм».

Рассмотрим пример. Оценивается возможность вложения в два финансовых проекта «1» и «2». Экспертные оценки предполагаемых значений прибыли по проектам и их вероятности представлены в табл. 3.5.

Таблица 3.5

Значения прибыли по проектам, млн. руб., и их вероятности

	Проект 1	Проект 2
Вероятность, р	0,2	0,6	0,2	0,3	0,5	0,2
Прибыль, млн. руб.	80	120	210	0	160	250

Вычислим математическое ожидание (интегральный эффект) по обоим проектам.

Е₁ = 0,2 × 80 + 0,6 × 120 + 0,2 × 210 = 130.

Е₂ = 0,3 × 0 + 0,5 × 160 + 0,2 × 250 = 130.

Т.о., математические ожидания по проектам равны.

Рассчитываем среднеквадратичное отклонение:

σ₁ = √0,2(80 - 130)² + 0,6(120 - 130)² + 0,2(210 - 130)² = √500 + 60 + 80 = 25,30.

σ₂ = √0,3(0 - 130)² + 0,5(160 - 130)² + 0,2 (250 - 130)² = √0 + 450 + 2880 = 57,71.

Т.о., среднеквадратичное отклонение (вариабельность) для второго проекта более чем в 2 раза превышает аналогичный показатель первого проекта. Т.о., нужно принять проект 1.

Если усложнить условие задачи, то решение может измениться.

Пусть известно, что у компании имеется непогашенная задолженность в размере 240 млн. руб. Какой проект она должна выбрать в таком случае?

Применим правило «трех сигм» для определения вероятного диапазона прибыли:

Проект 1: 130 ± 3 × 25,3, т.е. 54,2 < Прибыль₁ < 205,9.

Проект 2: 130 ± 3 × 57,71, т.е. -43,13 < Прибыль₂ < 303,19.

Т.о., приняв первый проект, компания ни в каком случае не сможет освободиться от долгов. При принятии второго проекта у нее есть вероятность погасить все долги и получить некоторую чистую прибыль.