Виды взаимосвязей, изучаемых в статистике. Задачи корреляционного анализа. Метод аналитических группировок.

Статистические показатели могут состоять между собой в следующих основных видах связи: факторной, компонентной, балансовой.

Вфакторной связи показатели выступают как факторы, воздействующие на другие показатели или как результативные, испытывающие на себе влияние других.

Факторные связи могут рассматриваться как функциональные и корреляционные.

При функциональной связи изменение результативного признака y полностью зависит от изменения факторного признака x: y=f (x)- это связь жесткая. Знание функциональных зависимостей позволяет достаточно точно прогнозировать события.

При корреляционной связи значение результативного признака y частично зависит от факторного признака x, т.к. возможно влияние других факторов. Корреляционные связи- соотносительные-, неполные. В них одному значению признака- фактора может соответствовать несколько значений результативного признака.

Компонентные связи характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:

a=b∙c

Балансовая связь-показателей характеризует зависимость между источниками формирования ресурсов (средств) и их использованием описывается формулами вида:

a+b=c+d- баланс (равенство обеих частей).

При изучении корреляционной связи статистических показателей решаются следующие задачи:

1. Обнаружение зависимости между факторным и результативным признаками и установление формы связи

2. Установление силы (тесноты) связи, т.е. степени приближения ее к функциональной.

Первая задача решается соответствующей обработкой материала и выводом уравнения корреляционной связи, а вторая – расчетом специальных показателей тесноты связи.

Метод аналитических группировок служит для выявления корреляционной зависимости между отдельными признаками элементов совокупности. Для этого совокупность разбивают на группы по значению признака – фактора и в каждой группе определяют среднее значение результативного признака. Если с изменением признака-фактора закономерно меняется средняя величина результативного признака, то между ними есть связь. Для количественного измерения тесноты связи между факторным и результативным признаками находим коэффициентдетерминации и корреляционное отношение.

Коэффициент детерминации:

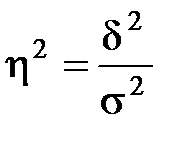
d² – дисперсия групповых уровней,

s² – среднегрупповая дисперсия

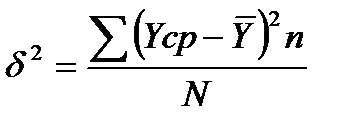
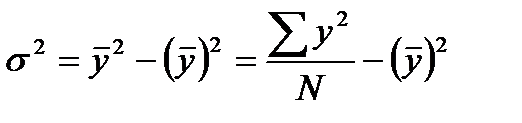
где у_ср – групповые средние, у - общая средняя.

Коэффициент детерминации показывает насколько признак-фактор определяет результативный признак.

Корреляционное отношение

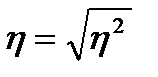
Корреляционное отношение показывает тесноту связи между исследуемыми признаками.

если h = 1, то связь функциональна,

если h = 0, то связь отсутствует,

если 0 < h < 1, то связь корреляционная.