Вероятностный прогноз случайной величины А

А	а1	а2	…	аn
Р (А)	p1	p2	…	pn

Математическое ожидание ;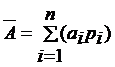

Дисперсия (вариация, среднеквадратичный разброс):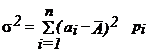

Стандартная девиация ( среднее квадратичное отклонение) .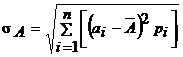

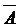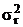После определения и выбор варианта производится по правилу Г. Марковица: проект 1 лучше проекта 2, если для него выполняется одно из следующих двух условий:

· 1) ;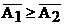

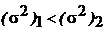
· 2) ;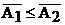

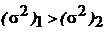
Стандартное относительное отклонение (коэффициент вариации)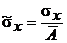

Задачи

1. Целью предприятия является получение годовой прибыли в размере 10 млн руб. Управляющие разработали три сценария развития предприятия: пессимистичный, наиболее реальный и оптимистичный. Если события с вероятностью 30 % будут развиваться по пессимистичному сценарию, то годовая прибыль предприятия составит 5 млн руб. Если события с вероятностью 50 % будут развиваться по наиболее реальному сценарию, то годовая прибыль предприятия составит 10 млн руб. Оптимистичный сценарий в случае его реализации с вероятностью 20 % принесет годовую прибыль в размере 15 млн руб. Предприятие в процессе осуществления своей финансово-хозяйственной деятельности не привлекает заемные средства.

Определить величины производственного и общего рисков.

Ответ:

2. Имеются два объекта инвестирования. Величина требуемых капитальных вложений одинакова. Величина планируемого дохода в каждом проекте неопределенна и приведена в виде следующего распределения. Какой объект предпочтительнее по доходности? По риску?

Проект А	Проект В
Доход	Вероятность	Доход	Вероятность
	0,1		0,10
	0,15		0,25
	0,40		0,35
	0,20		0,20
	0,15		0,10

Ответ:

3. Имеются данные о трех ценных бумагах. Первая бумага – облигация компании А с погашением через 15 лет; вторая – краткосрочный государственный вексель с погашением через 90 дней; третья – государственная облигация с погашение через 15 лет. Известно, что доходность каждой ценной бумаги либо 6 %, либо 7,5 %, либо 9,2 %. Распределите эти доходности между упомянутыми ценными бумагами. Дайте объяснение Вашему выбору.

Ответ:

4. Экспертами представлены данные об ожидаемой доходности акции А и В в зависимости от общеэкономической ситуации:

Экономическая ситуация	Вероятность	Доходность акций А, %	Доходность акций В, %
Быстрый рост экономики	0,15
Умеренный рост экономики	0,45
Нулевой рост экономики	0,30
Спад	0,10

Рассчитайте, какие акции выгоднее приобрести?

Ответ:

5.Оценивая две акции А и Б, инвестор пришел к выводу, что распределение вероятностей их ожидаемой доходности можно представить следующим образом:

Варианты прогноза	Вероятность	Доходность, %
акция А	акция Б	акция А	акция Б
Оптимистический	0,3	0,3
Реалистический	0,4	0,4
Пессимистический	0,3	0,3	-70

Какая акция предпочтительнее?

Ответ:

6.Текущая рыночная стоимость чисто дисконтной облигации равна 90 долл. Распределение вероятностей стоимости этой облигации через два года выглядит так:

рi	0.05	0.1	0.30	0.30	0.25
Vi

Определите ожидаемую доходность и стандартное отклонение доходности данной облигации за два года.

Ответ:

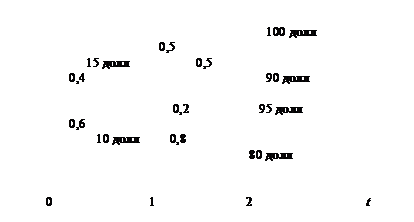
7.Дана двухлетняя облигация стоимостью 100 долл. На рисунке показано вероятностное распределение доходов от облигации. Определите ожидаемую доходность и стандартное отклонение облигации за два года.

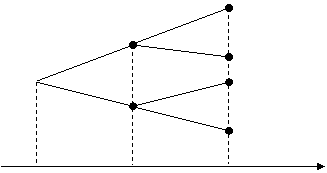Ответ:

8. Определите, какая из акций является наиболее рискованной:

Вероятность получения дохода	Ожидаемые ставки доходности по акциям, %
А	Б	В
0,1
0,3
0,4
0,2

Ответ:

9.При вложении капитала в мероприятие А из 10 случаев была получена прибыль: 14 млн. руб. – в одном случае; 12 млн. руб. – в одном случае; 10 млн. руб. – в одном случае; 8 млн. руб. – в одном случае; 6 млн. руб. – в одном случае; 5 млн. руб. – в двух случаях; 3 млн. руб – в трех случаях. Чему равно математическое ожидание и коэффициент вариации прибыли?

Ответ:

10.Фирма предполагает вложить средства либо в ценные бумаги с разным уровнем доходности, либо в инвестиционные проекты типов 1 и 2. Специалисты определили также следующие наиболее вероятные значения доходности по каждому виду вложений средств для разных типов состояний экономики. Определите лучший вариант вложения денежных средств.

Состояние экономики	вероятность	доходность , %
ГКО	Корпоративные облигации	Проект 1	Проект 2
Глубокий спад	0,05	8,0	12,0	-3,0	- 2,0
Незначительный спад	0,2	8,0	10,0	6,0	9,0
Стагнация	0,5	8,0	9,0	11,0	12,0
Незначительный подъем	0,2	8,0	8,5	14,0	15,0
Сильный подъем	0,05	8,0	8,0	19,0	26,0

Результаты представьте в виде таблицы

Состояние экономики	ГКО	Корпоративные облигации	Проект 1	Проект 2
Ожидаемая доходность, %
Дисперсия, %
Среднеквадратичное отклонение, %
Максимальная доходность, %
Минимальная доходность, %
Коэффициент вариации

11.Владелец груза, который следует перевезти морским транспортом, знает, что в результате возможной гибели корабля он теряет груз стоимостью 100 млн. руб. Ему также известно, что вероятность кораблекрушения 0,05; страховой тариф при страховании груза составляет 3% от страховой суммы.

Стоит ли владельцу груза: страховать свой груз?

Ответ:

12.Предприниматель стоит перед выбором, сколько закупить товара: 500 единиц или 1000 единиц. При покупке 500 единиц товара затраты составят 2000 руб. за единицу, а при покупке 1000 единиц товара затраты составят 1200 руб. за единицу. Предприниматель будет продавать данный товар по цене 3000 руб. за единицу. Однако он не знает, будет ли спрос на товар. При отсутствии спроса ему придется значительно снизить цену, что нанесет убыток его операции. При продаже товара вероятность составляет “50 на 50”, т. е. существует вероятность 0,5 для продажи 500 единиц товара и 0,5 для продажи 1000 единиц товара.

Определите стоимость полной информации.

Ответ:

13.Фирма оценивает возможность производства нового товара А со сроком использования 2 года. Величина денежного потока зависит от спроса на данный товар. Древо вероятностей возможных будущих денежных потоков, связанных с новым товаром, имеет вид

1 год	2 год
Исходная вероятность	Ожидаемый прогноз денежного потока, руб.	Исходная вероятность	Ожидаемый прогноз денежного потока, руб.
0,4		0,3
0,7
0,6		0,4
0,6

Стоимость товара 100 рублей. Оцените ожидаемую прибыль через:

А) год;

Б) два года.

Ответ:

14.В результате пожара сгорел производственный цех, в котором находились сырье, полуфабрикаты и готовая продукция на сумму 5 млн. руб. и оборудование на сумму 20 млн. руб. Затраты на разборку сгоревшего здания и уборку в цехе, т. е. на ликвидацию последствий пожара, составляют 0,5 млн. руб. Затраты на ремонт здания — 3 млн. руб., на ремонт и приобретение нового оборудования взамен сгоревшего — 6,5 млн. руб. Рассчитайте общую величину убытка.

Ответ:

15.Выберите вариант вложения капитала:

Номер события	Полученная прибыль, тыс. руб.	Число случаев, ед
Мероприятие А
Мероприятие Б

Ответ:

16.Рассчитайте коэффициент риска и выберите наименее рисковый вариант вложения капитала.

Вариант А – собственные средства предпринимателя – 5000 руб. Максимально возможная сумма убытка – 3500 руб;

Вариант Б – собственные средства предпринимателя – 30000 руб. Максимально возсожная сумма убытка – 12000 руб.

Ответ:

17.Какой образец мотоцикла запустить в серию? Разберите четыре критерия принятия решения: оптимистический, пессимистический, средней прибыли, минимальной упущенной выгоды. Прибыль фирмы от выпуска различных образцов (млн. руб.) представлена в таблице

Цена бензина	Мотоцикл «Витязь»	Мотоцикл «Комар»
Низкая (20%)
Средняя (60%)
Высокая (20%)

Ответ:

18.Какой образец автомобиля запустить в серию? Разберите четыре критерия принятия решения: оптимистический, пессимистический, средней прибыли, минимальной упущенной выгоды. Прибыль фирмы от выпуска различных образцов (млн. руб.) представлена в таблице

Цена бензина	Автомобиль «Алеша»	Автомобиль «Добрыня»
Низкая (40%)
Высокая (60%)

Ответ:

19.Капитал компании составляет 100 млн долл. США; максимально допустимый утвержденный размер единовременных потерь компании — 20% от капитала. На основании исторического анализа, проведенного риск-менеджером, было определено, что максимальный размер потерь при заключении подобной сделки может составлять 50% от размера сделки. Рассчитайте страховой запас.

Ответ:

20.При вложении капитала в некоторое мероприятие А из 200 случаев прибыль в 25 тыс. руб. была получена в 20 случаях; прибыль в 35 тыс. руб. – в 80 случаях; прибыль в 40 тыс. руб. – в 100 случаях. При вложение капитала в некоторое мероприятие В из 240 случаев прибыль в 30 тыс. руб. была получена в 144 случаях; прибыль в 35 тыс. руб. - в 72 случаях; и 45 тыс. руб. – в 44 случаях. Выберите вариант вложения капитала.

Ответ:

21.Мероприятие А требует вложения собственных средств в размере 5000 тыс.руб. и максимально возможная сумма убытка составит 3500 тыс. руб. Мероприятие В требует вложений собственных средств 30000 тыс. руб. и максимально возможная сумма убытка составит 12000 тыс. руб. выберите наименее рисковый вариант вложения собственных средств.

Ответ:

22.Рассмотрим работу швейного предприятия, выпускающего повседневную одежду, сбыт которой зависит от состояния погоды. Предприятие смогло получить более точную информацию о состоянии погоды за последние одиннадцать лет. Обычная погода бывает с вероятностью 0,2, прохладная – 0,3, и теплая – с вероятность. 0,5. Вероятностная платежная матрица (средняя прибыль, тыс. руб) представлена в таблице.

вероятность	0,	0,	0,5
Стратегия природы	обычная	прохладная	теплая
Стратегия предприятия
Обычная
Прохладная
Теплая

Рассчитайте стоимость информации о состоянии погоды, если максимальная ожидаемая денежная оценка при неполной информации равна 20833 тыс. руб.

Ответ:

23.Имеется информация о доходности ценных бумаг компаний за несколько лет (%):

Год Компания
А
Б
В

Вложения в ценные бумаги какой компании менее рискованны ?

Ответ:

24.Фирме необходимо выбрать лучший из двух альтернативных финансовых активов, если имеются следующие их характеристики:

Показатель	Вариант А	Вариант В
Цена ценной бумаги, тыс. руб. Доходность (экспертная оценка), % / вероятность: Пессимистическая Наиболее вероятная Оптимистическая Размах вариации доходности	14/0,2 16/0,6 18/0,2	13/0,2 17/0,6 21/0,2

Ответ:

25.Фирме необходимо выбрать лучший из 3 альтернативных финансовых активов, если имеются данные

Активы	Цена ценной бумаги, тыс. руб.	Доходность (экспертная оценка), /вероятность
А		13/0,1	15/0,4	16/0,3	17/0,2
В		14/0,3	15/0,3	16/0,4
С		12/0,1	14/0,4	15/0,2	17/0,2	18/0,1

Ответ:

26.Фирма А имеет сеть магазинов одежды в различных городах. Она могла бы приобрести магазин в приморском городе, что по подсчетам принесет среднюю чистую прибыль в 2500 тыс. руб. в год в последующие 5 лет, если в экономике продолжится спад, но в условиях экономического подъема прибыль может составить 6500 тыс. руб.. Альтернативой является приобретение магазина в Центральной части России, который мог бы обеспечить ежегодную прибыль в среднем в 3000 тыс. руб. в условиях экономического спада и 3500 тыс. руб. в условиях подъема. Экономические советники полагают, что шансы на экономический подъем составляют 60 %. Какой вариант предпочесть?

Ответ:

27.Компания, имеющая сеть закусочных, имеет возможность приобрести новую закусочную в одном из двух мест. В первом месте шансы на успех оцениваются в 0,7, и в этом случае ежегодная прибыл составит 800 тыс. Руб.. Если же эта закусочная не достигнет успеха, чистые убытки составят 50 тыс. Руб. В другом месте шансы на успех ниже – 0,6. В случае успеха открытие этой закусочной обеспечит компании чистую прибыль в размере 1200 тыс. руб., а в случае неуспеха убытки составят 100 тыс. руб.. Дайте рекомендацию относительно выбора места для приобретения новой закусочной.

Ответ:

28.У Ирины есть небольшой прилавок на рынке, где она продает пирожные. На настоящий момент у нее есть в запасе 240 пирожных на день торговли. Ей трудно прогнозировать спрос, поэтому она собада данные о ежедневной реализации своего товара за последние немколько месяцев.

Спрос за день, шт
Относительная частота данной величины спроса	0,2	0,2	0,4	0,2

Ирина решила закупать на день торговли запас пирожных в размере 180, 200 или 220 штук, но не уверена, какой именно уровень запаса будет самым прибыльным в долгосрочном плане. Каждое пирожное обходится ей в 4 рубля, а продает она их по 7 рублей. пирожное, не проданное к концу дня, отбраковывается. Рассчитайте, какой уровень запаса будет самым прибыльным составив платежную матрицу .

Уровень спроса	Величина прибыли
Запас 180	Запас 200	Запас 220

Ответ:

29.Компания «Русский стол» собирается построить новую фабрику, оснащенную современным обрудованием. Необходимо выбрать либо большую фабрику, либо маленькую. Прогноз спроса на мебель в долгосрочной перспективе предполагает, что шансы на высокий спрос мебели равны 50 %, на средний спрос – 30 %, а вероятность низкого спроса – 20 %. В таблице показаны платежи, связанные с различными сценариями. Они представляют собой ежегодную прибыль, прогнозируемую в случае строительства фабрики.

спрос	Большая фабрика	Маленькая фабрика
Высокий
Средний
Низкий

Рассчитайте ожидаемую денежную стоимость, связанную с каждым из возможных решений и дайте рекомендацию о размере проектируемой фабрики.

Ответ:

30.Мария Ивановна продает пирожки. Она подсчитала, что за в понедельник продажи составляют 300 штук пирожков, во вторник , среду и четверг – 400 штук, а в пятницу и в субботу – 500 шт. в среднем каждый пирожок ей обходится в 2 рубля, а продает она их по 4 рубля. Если пирожки заканчиваются, то Мария Ивановна делает закупку в соседнем кафе по 3 рубля за штуку. Постройте платежную матрицу, показывающую прибыль Марии Ивановны при различных уровнях спроса, когда запас составляет 300, 400 и 500 пирожков. Дайте рекомендации относительно оптимального запаса на день.

Ответ:

1. Портфель ценных бумаг

Ожидаемая доходность портфеля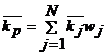

Дисперсия портфеля, состоящего из двух видов активов:

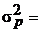
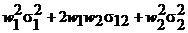
Ковариация .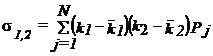

Корреляция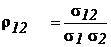

Дисперсия портфеля для случая с N активами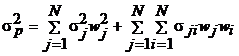

Доходность конкретного финансового рынка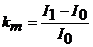

I₁, I₀ – значения фондовых индексов соответственно на конец и начало периода;

β-коэффициент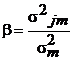

σ²_jm – ковариация между доходностью акции j и рыночной доходности, определяемой по динамике рыночного индекса;

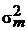- дисперсия рыночной доходности.

Модель САРМ: k_e = k_rf + b(k_m –k_rf)

k_e – ожидаемая доходность акций данной компании;

k_rf -доходность безрисковых ценных бумаг;

k_m – ожидаемая доходность в среднем на РЦБ;

b - риск ценной бумаги.

(k_m –k_rf) –премияза риск вложения своего капитала в рисковые ценные бумаги.

(k_е –k_rf) – премия за риск вложения капитала в бумаги данной компании

Задачи

1.Портфель инвестора состоит из ценных бумаг со следующими характеристиками:

Актив	Общая рыночная стоимость, долл.	β-коэффициент
А	50 000	0,0
В	10 000	0,9
С	25 000	1,1
D	8 000	1,2
Е	7 000	1,7

Доходность безрисковых ценных бумаг равна 7 %, доходность на рынке в среднем 14 %. Рассчитайте доходность портфеля.

Ответ:

2. Рассчитайте доходность портфеля состоящего из 300 акций фирмы А с доходностью 8 %, 500 акций фирмы В с доходностью 12 % и 1150 акций фирмы С с доходностью 6,7 %.

Ответ:

3.По модели оценки доходности финансовых активов (CAMP) найдите цену собственного капитала фирмы при следующих условиях: безрисковая ставка доходности финансовых активов составляет 8 % годовых; среднерыночная ставка доходности финансовых активов – 15 %; степень риска, связанная с вложением денежных средств в собственный капитал равна 2,5.

Ответ:

4.Оцените премию за риск по акции, имеющей значение β-коэффициентом 1,3, если рыночная премия за риск равна 10 %

Ответ:

5.Можно ли использовать акции А и Б (см. задачу 5, часть 4) для диверсификации портфеля?

Ответ:

6.Строится портфель из двух активов А и Б со следующими характеристиками:

	А	Б
Ожидаемая доходность	12 %	18 %
Стандартное отклонение	25 %	40%
Коэффициент корреляции	0,8

Оцените ожидаемую доходность и стандартное отклонение для портфеля с равными долями инвестирования.

Ответ:

7. Компания, имеющая β = 2,5 собирается привлечь дополнительный собственный капитал путем эмиссии обыкновенных акций. Доходность ГКО 6,25 %, средняя доходность рынка 14,0 %. Чему должна быть равна премия за риск вложения в акции данной компании?

Ответ:

8.Даны две ценные бумаги А и В со следующими параметрами. Какую ценную бумагу вы предпочтете и почему?

А )	А	Б
Ожидаемая доходность	50 %	6,5%
Стандартное отклонение	15 %	2 %

Б)	А	Б
Ожидаемая доходность	30 %	30 %
Стандартное отклонение	10 %	6 %

В)	А	Б
Ожидаемая доходность	15 %	10 %
Стандартное отклонение	5 %	5%

Ответ:

9. Фактическое значение индекса S&P 500 составило на 10 мая 2000 года 1384,29, на следующий день оно достигло уровня 1401,74. Определите дневную доходность “средней” акции на рынке .

Ответ:

10. Постройте график зависимости доходности портфеля состоящего из двух акций А и Б, со следующими характеристиками: k_А = 10 %, k_Б = 20 %, s_А = 0,2, s_Б = 0,6 в зависимости от риска портфеля, если коэффициент корреляции равен а) – 1, б) 0; в) + 1

Веса инвестирования, %	Ожидаемая доходность портфеля kp, %	Риск портфеля σр, %
w А	w Б

11.Оцените доходность акции с β = 0,8, если среднее значение рыночной доходности за прошлые годы равно 20 %, а безрисковая доходность – 7 %. Если экспертная доходности фондового рынка на будущий год на 20 % выше, чем средняя оценка по прошлым годам, то на сколько процентных пунктов следует ожидать увеличение доходности акции?

Ответ:

12.Инвестиционная копания использует самую простую стратегию управления активами, инвестируя только в два вида акций: в рисковые акции А и безрисковые акции Б.доходность рисковых акций равна доходности в среднем по рынку 22 %. Безрисковая доходность 10 %. Если менеджер ставит целью обеспечить доходность 15 % годовых, то как будут распределены средства между акциями А и Б? Чему равно значение β-коэффициента?

Ответ:

13 . Портфель состоит из 200 акций фирмы А, 400 акций фирмы В, и 1050 акций фирмы с. Текущие рыночные цены акций соответственно 20, 50 и 15 долларов. Рассчитайте структуру и доходность портфеля

Ответ:

14. Акция А имеет ожидаемую доходность 12 % и среднее квадратичное отклонение – 7% соответствующие значения этих показателей для акции В – 18 и 30 %; коэффициент корреляции между ожидаемыми доходностями акций составляет 0,7. Рассчитайте ожидаемую доходность и среднее квадратичное отклонение портфеля, состоящего на 35 % из акций А и 65 % акций В.

Ответ:

15. Акции компании А имеют β =1,6. Безрисковая процентная ставка и норма прибыли на рынке в среднем соответственно равны 11 и 15 %. Последний выплаченный дивиденд равен 3 доллара на акцию, причем ожидается, что он будет постоянно возрастать с темпом g= 5 % в год. Чему равна ожидаемая доходность акций компании? Какова рыночная цена акции.

Ответ:

16. В инвестиционном портфеле акционерного общества три акции компании «А», две акции компании «Б» и пять акций компании «В» с одинаковыми курсовыми стоимостями. Как изменится стоимость инвестиционного портфеля, если курс акций компании «А» увеличится на 18%, «Б» — на 16% и «В» — упадет на 15%?

Ответ:

17.Приведены данные о доходности акций компании «Бест Продакт» за 10 кварталов, а так же данные о доходности рынка за этот период. Вычислите показатель β-коэффициент

квартал	Доходность акций компании «Бест Продакт»	Доходность рынка
	3,8	2,7
	5,3	3,1
	-7,2	-4,9
	10,1	9,9
	1,0	3,7
	2,5	1,2
	6,4	3,8
	4,8	4,0
	6,0	5,5
	2,2	2,0

Ответ:

18.На основе данных, представленных в таблице, определите факторβ-коэффициента обыкновенных акций и сделайте обоснованный вывод о степени риска каждого денежного инструмента, если известно, что фактическая средняя рыночная доходность ценных бумаг составляет 8 %.

акция	Доходность, %
А
Б
В
Г

Ответ:

19. Портфель инвестора состоит из обыкновенных акций компаний А, В и С. Определите ожидаемую доходность портфеля через год по следующим данным

компания	Количество акций в портфеле, шт	Рыночная цена акции, руб.	Ожидаемая цена через год, шт
А
В
С

20. Определите β-коэффициент инвестиционного портфеля, если имеются следующие данные по его структуре:

Актив	Доля актива в портфеле, %	β-коэффициент актива
А		0,5
В		1,2
С		0,8

Ответ:

21. Коэффициент β некоторой фирмы М равен 1,6, безрисковая ставка доходности 9 %, предполагаемая доходность рынка равна 13 %. Чему будет равна доходность акций этой фирмы по модели САРМ?

Ответ:

22.Компания А это холдинговая компания с четырьмя подразделениями. Доли бизнеса, приходящиеся на каждое ее подразделение, и их соответствующие бета-коэффициенты представлены в таблице.

Подразделение	Доля актива в портфеле, %	β-коэффициент
Производство электрических установок	0,6	0,7
Производство кабеля	0,25	0,9
Недвижимость	0,1	1,3
Специализированные проекты	0,05	1,5

Каков бета-коэффициент компании А? Предположим, что безрисковая ставка доходности равна 6 %, а премия за рыночный риск – 5 %. Какова будет требуемая доходность для акций данного холдинга?

Ответ:

23.Если компания А (см. задачу 22) изменит свою политику: сократит бизнес электрических установок до 50 % в то же самое время она будет развивать направление специализированных проектов, которые будут занимать до 1 5% от всего объема производства. Какова будет теперь требуемая инвесторами норма доходности?

Ответ:

24.Вы планируете инвестировать в ценные бумаги сумму в 200 тыс. долл.. в Вашем распоряжении имеется два вида ценных бумаг, а и В, и вы можете формировать произвольный портфель, состоящий из этих ценных бумаг вы прогнозируете следующее вероятностное распределение доходности ценных бумаг А и В

Вероятность события,	Доходность А, %	Доходность В, %
0,1	- 10	- 30
0,2
0,
0,2
0,1
	kА = ?	kВ = 20,0
	σА,= ?	σВ, = 25,7

Используя приведенные данные найдите k_А и σ_А. Постройте график достижимого множества портфелей ценных бумаг и определите его эффективную границу.

Ответ:

25.Инвестор вложил 35 тыс. долл. в акции с бета-коэффициентом 0,8, и 40 тыс. долл в акции с бета-коэффициентом 1,4. если эти ценные бумаги – единственное вложение инвестора, каков будет бета-коэффициент его портфеля?

Ответ:

26.Вы владеете диверсифицированным портфелем ценных бумаг, при этом ваши вложения составляют по 75 тыс. долл в каждый из 20 различных видов обыкновенных акций. Бета-коэффициент портфеля составляет 1,12. Вы решили продать часть акций из состава портфеля на сумму 75 тыс. долл и использовать эти средства для приобретения других акций. Бета-коэффициент проданных акций был равен 1,0, а для новых акций он равен 1,75. вычислите новый бета-коэффициент своего портфеля в целом.

Ответ:

27.Определить риск портфеля, состоящего из двух активов, если доля первого составляет 70%, а дисперсия = 4%, доля второго = 30%, а дисперсия равна 3.8%, коэффициент корреляции =1. Как изменится риск нового портфеля, если в него добавить безрисковый актив, равный по своей доле 20% от старого портфеля?

Ответ:

28.Определить целесообразность инвестирования в акции компании с помощью модели САРМ при исходных данных

Акции компании	b	Кrf, %	Кm, %
А	0,6
В	0,8
С	1,1
Д	1,2

Ответ:

29.Проанализировать риск имеющихся финансовых инструментов по одной из двух стратегий: а) при обособленном выборе актива; б) при сочетании двух активов, - при исходных данных.

Портфель	Доходность портфеля по годам	Коэффициент корреляции, r
А				-
В				-
С				-
А+В (50%+50%)
А+С (50%+50%)				-1
В+С(50%+50%)				0,5

Ответ:

30.Портфель инвестора состоит из ценной бумаги А имеющей среднеквадратичное отклонение 15 %, и ценной бумаги В, имеющей среднеквадратичное отклонение 14 %. Веса активов в портфеле одинаковы. Рассчитайте риск портфеля если коэффициент корреляции между бумагами равен: 1, 0,6; -1.

Ответ:

31.Портфель инвестиций инвестора имеет следующую структуру:

- облигации государственного займа 30 %;

- простые акции крупных нефтяных корпораций 10 %;

- привилегированные акции банков – 20 %;

- депозитные сертификаты коммерческих банков 20 %;

- облигации крупных промышленных предприятий 20 %

Определите тип портфеля инвестиций: консервативный или агрессивный.

Ответ:

32.В инвестиционном портфеле 300 акций эмитента А, 200 акций эмитента В, 400 акций эмитента С с примерно равными долями инвестирования. Как измениться стоимость портфеля, если курсы акций а и С упадут на 10 и 20, а курс акций В вырастет на 15 % соответственно?

Ответ:

33.Вычислите ожидаемую доходность портфеля.

Наименование цб	Количество акций в портфеле, ед	Начальная рыночная цена одной акции, $	Ожидаемая стоимость одной акции в конце периода, $
А			46,48
В			43,61
С			76,14

Ответ: 22 %

Каков коэффициент бета для каждой акции из нижеприведенной таблицы?

Акция	Ожидаемая доходность акции, если рыночная доходность равна -10%	Ожидаемая доходность акции, если рыночная доходность равна +10%
А		+20
Б	-20	+20
В	-30
Г	+15	+15
Д	+10	-10

3. Предположим, что стандартное отклонение рыночной доходности равно +20%.

· · Каково стандартное отклонение доходности диверсифицированного портфеля с коэффициентом бета 1,3?

· · Каково стандартное отклонение доходности диверсифицированного портфеля с коэффициентом бета 0?

· · Стандартное отклонение хорошо диверсифицированного портфеля составляет 15%. Каков его коэффициент бета?

· · Стандартное отклонение плохо диверсифицированного портфеля составляет 20%. Каков его коэффициент бета?

6. Управление запасами и денежными средствами

Финансовый цикл предприятия

t_ф.ц = t_о.ц. – t_о.КЗ = t_о.ТМЗ + t_о.ДЗ – t_о.КЗ

где t_о.ц. – продолжительность операционного цикла;

t_о.КЗ. – время обращения кредиторской задолженности;

t_о.ТМЗ – время обращения производственных запасов;

t_о.ДЗ – время обращения дебиторской задолженности;

Управление запасами

ТС = С_{выполнения} + С_{хранения} +С _{запасов} Cхр + С вып → min

,

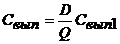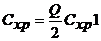
ТС – общие затраты;

Оптимальный размер запаса

= ,

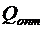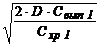где Q — число единиц партии заказа;

Р – стоимость покупки единицы запасов;

D — общая потребность единиц материала на период (спрос);

C_{вып 1} — стои