Выведение товара на рынок; 2 – рост; 3 – зрелость; 4 – упадок; 5 – реанимация спроса.

Внутригодовая цикличность носит часто сезонный характер.

При изучении сезонных процессов часто применяется спектральный анализ, который позволяет прогнозировать тенденции, динамика которых содержит колебательные или гармонические составляющие [31].

Сезонные волны можно описать гармоникой ряда Фурье:

(2.9)

,

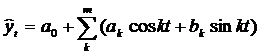где t – номер гармоники ряда Фурье;

a₀ и a_k, b_k – определяют по МНК;

k – число гармоник (1, 2, …)

В условиях переходной экономики возрастает значимость прогнозирования жизненного цикла товара (ЖЦТ). Автором концепции ЖЦТ считается известный маркетолог Теодор Левитт, предложивший ее в 1965г.

Суть прогноза заключается в том, чтобы определить, как надолго и насколько интенсивно будет сохраняться спрос на данный товар. Прогноз ЖЦТ – многоплановый процесс, важной составляющей которого является подбор для каждого этапа соответствующей трендовой модели, отражающей не только рост, стабилизацию или спад, но и степень ускорения или замедления этих процессов. Такой прогноз является составным элементом прогнозирования покупательного спроса и рыночной конъюнктуры.

Жизненный цикл товара можно графически смоделировать в виде сложной кривой (рис. 2.3).

Математически смоделировать весь жизненный цикл товара практически невозможно, пришлось бы использовать сложную многочленную функцию, которую трудно интерпретировать. Целесообразно использовать метод линейно-кусочных агрегатов, то есть моделировать и прогнозировать каждый этап ЖЦТ с помощью трендовой и (или) многофакторной модели, отражающей закономерности каждого этапа.

Отмеченные ранее методы механического выравнивания могут также выступать в роли самостоятельных методов статистического прогнозирования.

Прогнозирование на основе адаптивных скользящих средних производится с использованием следующих формул:

	(2.10)

,

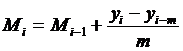где M_i – скользящая средняя, отнесенная к концу интервала.

(2.11)

.

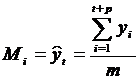Первый член уравнения (2.10) – М_i-1 несет «груз прошлого» - инерцию развития, а второй адаптирует среднюю к новым условиям. Таким образом, средняя как бы обновляется, «впитывая» информацию о фактически реализуемом процессе (степень обновления определяется весом 1/m).

Экспоненциальные средние. Влияние прошлых наблюдений должно затухать по мере удаления от момента, для которого определяется средняя. Для этой цели используют экспоненциальное сглаживание, применяемое в краткосрочном прогнозировании (идея Н.Винера):

(2.12)

,

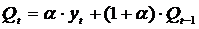где Q_t – экспоненциальная средняя на момент t;

a – коэффициент, характеризующий вес текущего наблюдения (параметр сглаживания).

При расчете по формуле (2.12) необходимо выбрать Q_t-1.. Часто Q_t-1 принимают равным yt.

Применение метода успешно, когда ряд имеет достаточно большое число уровней. Чем меньше a, тем больше роль «фильтра», поглощающего колебания 0< a £1. Практически диапазон a ограничивается величинами 0,1; 0,3. Хорошие результаты дает a = 0,1. При выборе a следует иметь в виду, что для повышения скорости реакции на изменение процесса развития необходимо повысить a, однако это уменьшает «фильтрационные» возможности средней.

Специфика экономических процессов состоит в том, что они обладают взаимосвязью и инерционностью (см. п. 1.3). Последнее означает, что значение фактического показателя в момент времени t зависит определенным образом от состояния этого показателя в предыдущих периодах, т.е. значения прогнозируемого показателя должны рассматриваться как факторные признаки. Уравнение авторегрессионной зависимости в общем имеет вид:

	(2.13)

,

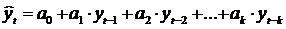где 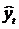– прогнозируемые значения показателя в момент времени t;

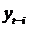– значения показателя y в момент времени (t-i);

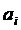– i-тый коэффициент регрессии.

Часто прогнозируемый показатель зависит не только от предшествующих состояний, но и от других факторов x. Тогда говорят о смешанной авторегрессии:

(2.14)

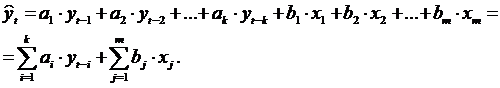
Оценки a_i и b_j находят по МНК.

Все приведенные выше модели позволяют получить точечные оценки. Для определения наиболее вероятных интервалов варьирования прогнозных показателей необходимо найти доверительные оценки. В общем виде расчет доверительного интервала может быть представлен следующим образом:

	(2.15)

,

где 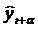– точечный прогноз;

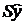– средняя квадратическая ошибка прогноза;

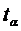– t-статистика Стьюдента;

a – период упреждения прогноза.

В общем виде для полиномов различных степеней:

	(2.16)

,

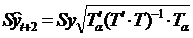где (Т¢×Т) – матрица системы нормальных уравнений;

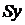– среднее квадратическое отклонение фактических значений от расчетных.

В частности, для линейного тренда:

(2.17)

,

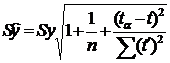где t_a – заданное на период упреждения значение переменной t, (t_a=n+a);

t – среднее значение t, т.е. значение порядкового номера уровня, стоящего в середине ряда;

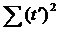– сумма квадратов отклонений значений независимой переменной от их средней.

Важно иметь в виду, что экстраполяция в рядах динамики носит приближенный и условный характер. Поэтому применение методов экстраполяции не должно становиться самоцелью, а при разработке социально-экономических прогнозов должна привлекаться дополнительная информация, на основе которой в полученные методом экстраполяции количественные оценки вносятся соответствующие коррективы.