Экономико-математическое моделирование
Методы экономико-математического моделирования применяются преимущественно в среднесрочном, а также в долгосрочном прогнозировании.
В данной группе методов можно выделить корреляционно-регрессионное моделирование, которое используется для объектов, имеющих сложную многофакторную природу (объем инвестиций, затраты, прибыль, объемы продаж и т.п.). Для осуществления регрессионного моделирования необходимо [39]:
- наличие ежегодных данных по исследуемым показателям;
- наличие одноразовых прогнозов, то есть таких, которые не корректируются с поступлением новых данных.
Наиболее разработанной в теории прогнозирования является методология так называемой парной корреляции, рассматривающей влияние факторного признака x на результативный y. Методы оценки параметров уравнения регрессии аналогичны приемам при экстраполяции (т.к. фактор времени t можно рассматривать как частный случай параметра x). На практике же гораздо чаще приходится исследовать зависимость результативного признака от нескольких факторных. В этом случае статистическая модель является многофакторной. Например, линейная регрессия с m независимыми переменными имеет вид
|
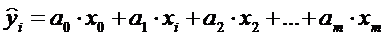 .
. Оценки параметров находят по МНК.
Отбор факторов для построения многофакторных моделей производится на основе качественного и количественного анализа социально-экономических явлений с использованием статистических и математических критериев.
Общепринятым является трехстадийный отбор факторов:
1. На первой стадии осуществляется априорный анализ, и на факторы, включаемые в состав модели, не накладываются ограничения.
2. На второй стадии производится оценка и отсев части факторов. Это достигается путем анализа парных коэффициентов корреляции и оценкой их значимости. Для этого составляется матрица парных коэффициентов корреляции (табл. 2.3).
Анализ таблицы ведется с использованием следующих критериев:
|
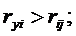
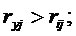
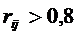 ,
, где rij – парные коэффициенты корреляции.
3. На заключительной стадии производят окончательный отбор факторов путем анализа значимости вектора оценок параметров различных вариантов уравнений множественной регрессии с использованием критерия Стьюдента
|
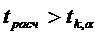 ,
,
где k – число степеней свободы,
a – уровень значимости.
В процессе анализа решается проблема мультиколлинеарности, которая заключается в том, что между факторными признаками может существовать значительная линейная связь, что приводит к росту ошибок оценок параметров регрессии.
Таблица 2.3
Матрица парных коэффициентов корреляции множественной
Модели регрессии
| y | x1 | x2 | … | xj | … | xm | |
| y | 1 | ry1 | ry2 | … | ryj | … | rym |
| x1 | r1y | 1 | r12 | … | r1j | … | r1m |
| x2 | r2y | r21 | 1 | … | r2j | … | r2m |
| … | … | … | … | … | … | … | … |
| xi | riy | ri1 | ri2 | … | 1 | … | rim |
| … | … | … | … | … | … | … | … |
| xm | rmy | rm1 | rm2 | … | rmj | … | 1 |
Приемы построения регрессионных и авторегрессионных моделей достаточно хорошо описаны в экономико-статистической литературе [15, 21, 35, 39, 48] и не являются предметом описания настоящего учебного пособия. Наличие прогрессивных информационных технологий позволяет достаточно оперативно рассчитывать параметры этих моделей.
Во внутрипроизводственном прогнозировании используются:
· модели внутренней среды фирмы, так называемые корпоративные модели;
· макроэкономические модели, к которым относят эконометрические модели, модели «затраты - выпуск» [1].
Корпоративные модели обычно представляют набор формул (уравнений), которые отражают отношение ряда переменных к определенному объекту, например к объему продаж.
В качестве примера рассмотрим анализ и прогнозирование конъюнктуры рынка отдельного товара (цифры условные).
Ситуация. На рынке сложилась ситуация, которую можно охарактеризовать с помощью трех индикаторов: индексов продажи, цен и объема товарооборота (табл. 2.4).
Таблица 2.4
