Доходность финансовой операции в условиях неопределенности

Доходность финансовой операции (см. формулу (1.1) зависит от множества факторов, которые можно объединить в следующие группы:

- политические и социальные;

- финансово-экономические;

- организационно-технические;

- отраслевые;

- природные факторы.

Политические и социальные факторы обусловлены политической и, как следствие, экономической и социальной нестабильностью внутри страны и в международных отношениях. Политическая нестабильность внутри страны связана с борьбой за власть различных партий, которые в борьбе за избирателей отстаивают различные модели социально-экономического развития. Во многих случаях это связано с лоббированием партийными фракциями интересов различных фирм и компаний. Возможность смены политического расклада в коридорах власти приводит к нестабильности налогового и хозяйственного законодательства. Возможная смена "правил игры" для хозяйствующих субъектов приводит к невозможности заранее однозначно прогнозировать результаты финансово-хозяйственной деятельности.

Нестабильность в международных отношениях обусловлена процессами глобализации экономики, отстаиванием странами своих геополитических интересов и обеспечением экономической безопасности. Это может приводить к введению политических и экономических санкций.

К социальным факторам относятся забастовки и криминогенная обстановка в стране и в отдельных ее регионах.

Финансово-экономические факторы. К этим факторам относят изменения ключевой ставки и ставки рефинансирования Центрального банка России; колебания курса валют; колебания годовых процентных ставок коммерческих банков по депозитам и кредитным операциям; колебания цен на энергоносители на мировом рынке, а также цен и тарифов на товары и услуги на внутреннем рынке; инфляционные процессы; распространение неплатежей и т. п.

Финансово-экономические факторы являются, как правило, следствием политической и социально-экономической ситуации как внутри страны, так и в международных отношениях.

Организационно-технические факторы. К этой группе факторов можно отнести: квалификацию управленческого персонала; недостаточное знание юридической базы совершения сделок и проведения схем финансово-хозяйственных операций; непроизводственные простои производственного оборудования; несоблюдение технологических нормативов эксплуатации оборудования, хранения сырья; возможность срыва сроков поставок оборудования, комплектующих и материально-производственных запасов.

Природные факторы. К этой группе факторов относятся землетрясения, наводнения, ураганы, смерчи, засухи, заморозки и другие природные и погодные катаклизмы.

Отраслевые факторы. Это факторы, присущие тем или иным отраслям хозяйственной деятельности. Так, для сельскохозяйственной отрасли существенными являются природные факторы; для рыбопромышленного комплекса существенным фактором является состояние эксплуатируемых биоресурсов, возможность ведения промысла в экономических зонах других государств, политика нашего государства в плане воспроизводства рыбопромысловых судов и т. п.

Совокупное действие всех этих факторов приводит к тому, что величина дохода 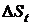(формула (2.1), получаемого после совершения финансово-хозяйственной операции, даже на ограниченном временном интервале t является случайной величиной. При реинвестировании получаемых доходов 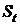на нескольких финансово-хозяйственных циклах суммарный доход определится формулой:

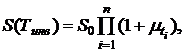(3.1)

где 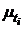- доходность финансовой операции на интервале длительностью 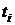цикла совершения финансово-хозяйственной операции.

При длительном инвестировании средств 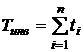условия хозяйствования и факторы, влияющие на финансовый результат, могут значительно изменяться на интервале инвестирования средств 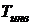. При этом суммарная доходность определяется формулой:

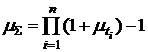(3.2)

и может изменяться под воздействием случайных факторов в значительных пределах.

Так как доходность финансовой операции (формула 1.1) определяется совокупным действием множества случайных факторов, доходность финансовой операции 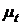и получаемый доход 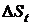в соответствии с центральной предельной теоремой теории вероятностей можно считать случайными величинами, имеющими нормальный закон распределения.

Плотность вероятности случайных величин 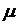и 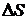может быть записана в виде:

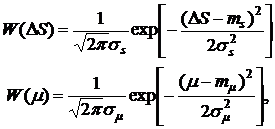(3.3)

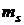где и 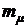- математическое ожидание (ожидаемое среднее значение) дохода 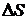и доходности 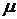соответственно;

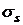и 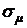- среднеквадратическое отклонение соответственно дохода 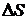и доходности 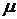от математического ожидания.

Чем больше среднеквадратическое отклонение 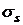(или 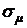), тем на большую величину фактически полученный доход (или доходность) может отличаться от ожидаемого среднего значения.

Оценим суммарную доходность 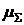финансовых операций на двух (n = 2) соседних интервалах инвестирования t₁ и t₂:

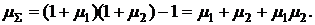(3.4)

Из формулы (3.4) видно, что суммарная доходность 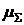определяется не только суммой доходностей на соседних интервалах 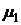и 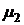, но и слагаемым 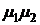, обусловленным так называемым синергетическим эффектом.

Если и являются случайными величинами, то их совместная плотность вероятности определяется формулой:

(3.5)

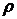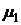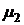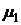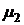где - коэффициент корреляции случайных величин и , характеризующий степень линейной взаимосвязи между значениями доходностей и на соседних интервалах инвестирования 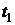и .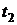

Коэффициент корреляции может принимать значения в интервале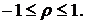

Формулы (3.4) и (3.5) позволяют определить математическое ожидание суммарной доходности 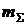и дисперсию 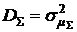. Для математического ожидания суммарной доходности получим:

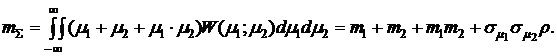(3.6)

Если случайные величины 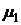и 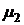независимы, то 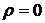и четвертое слагаемое в формуле (3.6) будет равно нулю. Но на практике доходности финансовых операци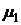й и 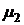на соседних временных интервалах инвестирования 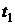и 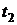, как правило, зависимы, причем, если при увеличении доходности 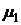наблюдается тенденция к увеличению доходности 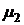, то 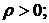если при увеличении доходности 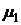наблюдается тенденция к уменьшению доходности 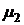, то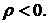

В реальной рыночной экономике ожидаемый средний уровень доходности имеет значение 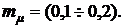Из этого следует, что третье слагаемое в формуле (3.6) на порядок меньше чем сумма первых двух слагаемых, т. е. увеличение суммарной доходности 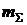за счет синергетического эффекта имеет незначительную величину. На основании данного вывода третьим слагаемым в формуле (3.4) можно пренебречь. В этом случае суммарную доходность 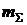при 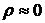можно определять суммой доходностей инвестиций на интервалах :

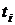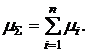(3.7)

Если доходности 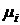являются независимыми случайными величинами, имеющими нормальный закон распределения с числовыми характеристикам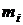и и 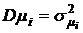, то с учетом равенства (3.7) можно считать, что суммарная доходность будет иметь нормальный закон распределения плотности вероятности (формула (3.3) с математическим ожиданием и дисперсией, определяющимися формулами:

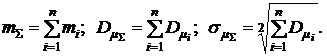(3.8)