Коэффициенты приведения и наращения рент

Рента постнумерандо

Финансовый поток постоянной ренты постнумерандо можно записать в виде:

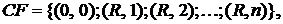
где R – размер платежей.

Графическое представление постоянной годовой ренты постнумерандо приведено на рис. 2.2.

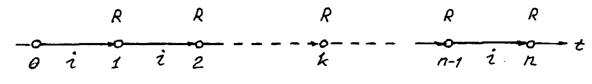
Рис. 2.2. Конечная годовая постоянная рента постнумерандо

Найдем современную стоимость ренты 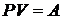постнумерандо. В соответствии с формулой (2.2) получим:

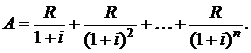(2.4)

В правой части равенства (2.4) имеем сумму членов убывающей геометрической прогрессии со знаменателем и первым членом 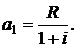Сумма n-членов геометрической прогрессии определяется формулой:

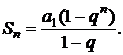(2.5)

С учетом значений а₁ и q для современной стоимости ренты постнумерандо получим:

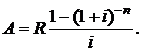(2.6)

Множитель при R называют коэффициентом приведения ренты и обозначают :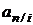

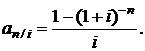(2.7)

Наращенная конечная сумма ренты обозначается 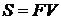и определяется суммой (2.3):

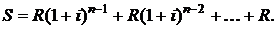
Данная сумма является суммой n-членов возрастающей геометрической прогрессии со знаменателем 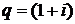и первым членом R. В соответствии с формулой (2.5) получим:

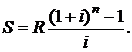(2.8)

Множитель при R называют коэффициентом наращения и обозначают :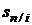

(2.9)

Из сравнения формул (2.7) и (2.9) следует:

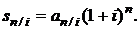(2.10)

Коэффициенты приведения 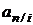и наращения 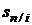зависят только от процентной ставки i и срока ренты n.

Из формулы (2.10) можно записать соотношение между конечной S и современной А стоимостью ренты постнумерандо:

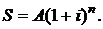(2.11)

Рента пренумерандо

Финансовый поток годовой постоянной ренты пренумерандо можно записать в виде:

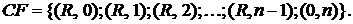
Графическое представление ренты пренумерандо приведено на рис. 2.3.

Рис. 2.3. Конечная годовая постоянная рента пренумерандо

Найдем современную стоимость ренты пренумерандо 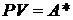. В соответствии с формулой (2.2) получим:

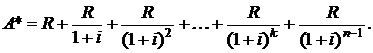
Современная стоимость ренты пренумерандо определяется как сумма n-членов убывающей геометрической прогрессии со знаменателем и первым членом 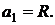С учетом значений 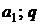формулы (2.5) для современной стоимости ренты пренумерандо получим:

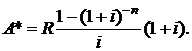(2.12)

Коэффициент приведения ренты пренумерандо определяется по формуле:

(2.13)

Наращенная сумма ренты пренумерандо в соответствии с формулой (2.3) определяется суммой:

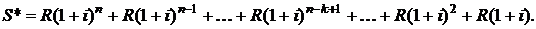
В правой части данного равенства имеем сумму n-членов возрастающей геометрической прогрессии со знаменателем 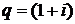и первым членом 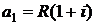. С учетом формулы (2.5) для конечной, наращенной суммы ренты пренумерандо получим:

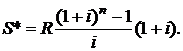(2.14)

Множитель при R является коэффициентом наращения ренты пренумерандо:

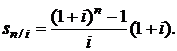(2.15)

Из формул (2.13) и (2.15) видно, что соотношение между коэффициентами наращения 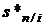и приведения 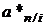определяется формулой, аналогичной формуле (2.10):

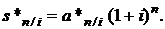(2.16)

Аналогичной формулой определяется соотношение между конечной наращенной 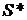и современной стоимостью 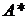ренты пренумерандо

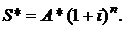(2.17)

Из сравнения формул (2.6) и (2.12) можно выявить связь между современными стоимостями рент пренумерандо и постнумерандо:

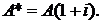(2.18)

Из сравнения формул (2.8) и (2.14) следует аналогичная формула для соотношения конечных наращенных стоимостей рассматриваемых рент:

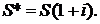(2.19)

Аналогичные соотношения можно получить для коэффициентов наращения и приведения рент постнумерандо и пренумерандо:

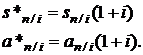(2.20)

Срочные ренты

Срочной называется рента, когда рентный платеж R производится не единовременно, один раз в год, а разбит на r одинаковых платежей, совершаемых r раз в год через равные промежутки времени.

Финансовый поток r-срочной ренты постнумерандо можно записать в виде:

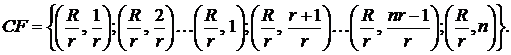
Графическое представление r-срочной ренты постнумерандо при r = 4 приведено на рис. 2.4:

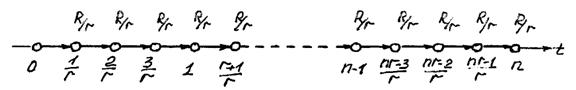
Рис. 2.4. r-срочная рента постнумерандо

Найдем современную стоимость r-срочной ренты постнумерандо, когда дисконтирование платежей осуществляется по схеме сложных процентов, т. е. множитель дисконтирования за один период 1/r будет равен (1 + i)^-1/r. С учетом данного множителя дисконтирования и формулы (2.3) для современной стоимости r-срочной ренты постнумерандо получим

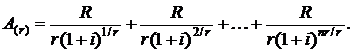
В правой части данного равенства имеем nr-членов убывающей геометрической прогрессии со знаменателем 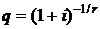и первым членом 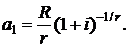С учетом формулы (2.5) для современной стоимости r-срочной ренты постнумерандо получим

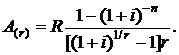(2.21)

Коэффициент приведения определяется множителем при R

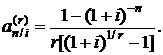(2.22)

Конечная, наращенная стоимость r-срочной ренты в соответствии с формулой (2.4) определится суммой

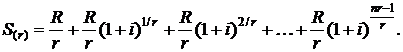
Данная сумма записана в обратном порядке, т. е. первым слагаемым является последний платеж, вторым слагаемым – предпоследний платеж, а последнее слагаемое определяется первым платежом с учетом его множителя наращения за nr-1 периодов. В правой части данного равенства имеем сумму nr-членов возрастающей геометрической прогрессии со знаменателем 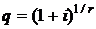и первым членом 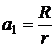с учетом формулы (2.5) для конечной, наращенной стоимости r-срочной ренты получим

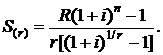(2.23)

Коэффициент наращения r-срочной ренты постнумерандо определяется формулой

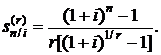(2.24)

Из сравнения формул (2.21) с (2.23) и (2.22) с (2.24) видно, что для современной и конечной стоимостей, а также коэффициентов приведения и наращения r-срочной ренты постнумерандо справедливы формулы:

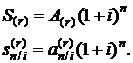(2.25)

Получим формулы для расчета современной и конечной стоимостей r-срочной ренты пренумерандо. Финансовый поток для данной ренты можно записать в виде

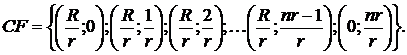
Современная стоимость r-срочной ренты пренумерандо с учетом формулы (2.3) может быть записана в виде суммы

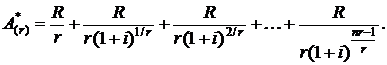
В правой части равенства имеем сумму nr-членов убывающей геометрической прогрессии со знаменателем 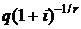и первым членом 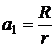, которая с учетом формулы (2.5) может быть записана в виде

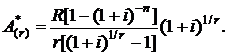(2.26)

Коэффициент приведения r-срочной ренты пренумерандо, являющийся множителем при R, определяется формулой

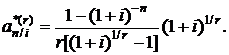(2.27)

Конечная стоимость r-срочной ренты пренумерандо с учетом формулы (2.4) может быть записана в виде

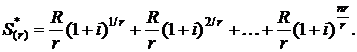
В данной формуле первое слагаемое определяет значение платежа 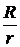, совершаемое в момент времени 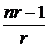, пересчитанное к окончанию срока ренты, а последнее слагаемое определяет значение платежа 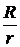, пересчитанное за nr периодов к окончанию срока ренты. Правая часть данного равенства является возрастающей геометрической прогрессией со знаменателем 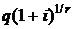, первым членом 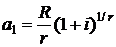, и ее сумма определяется формулой

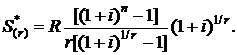(2.28)

Коэффициент наращения r-срочной ренты пренумерандо будет равен

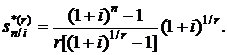(2.29)

Взаимосвязь между современной и конечной стоимостями, а также между коэффициентами наращения и приведения r-срочной ренты пренумерандо определяется аналогично формуле (2.25):

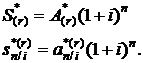(2.30)

При сравнении стоимостных показателей r-срочных рент постнумерандо и пренумерандо получим формулы

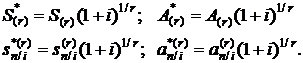(2.31)

2.4. Расчет r-срочной ренты при погашении кредита

Рассмотрим применение формул для определения стоимости r-срочной ренты при расчете графика аннуитета в погашении задолженности по кредиту. Расчет будем проводить для следующих условий. В банке взят кредит на сумму D рублей под годовую процентную ставку i сроком на n лет. Погашение кредита осуществляется r раз в год равными платежами размером R_r рублей.

В сумму платежа входят платеж в погашение тела кредита 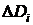и проценты за пользование кредитом 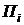. Сумма кредита D выплачивается ссудозаемщику единовременно в день подписания кредитного договора. Поток платежей в погашение кредита является r-срочной рентой постнумерандо.

Так как сумма кредита D выплачивается в момент времени t₀, то эта сумма, по сути, равна современной стоимости r-срочной ренты, выплачиваемой в погашение кредита

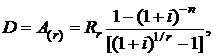(2.32)

где 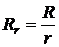- размер разового платежа.

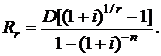(2.33)

В соответствии с формулой (1.8) определим сумму процентов П₁, выплачиваемых банку за пользование кредитом в сумме D рублей за время 1/r лет до первого платежа

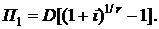(2.34)

Сумма 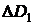, выплачиваемая в погашение тела кредита, будет равна

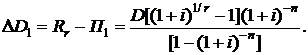(2.35)

Тогда сумма задолженности по кредиту после первого платежа составит

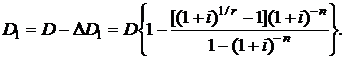(2.36)

Сумма процентов П₂, выплачиваемых за пользование кредитом при втором платеже, будет равна

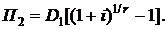(2.37)

Сумма 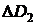, выплачиваемая в погашение тела кредита при втором платеже, определится разностью

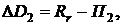
а задолженность по кредиту после второго платежа определится формулой

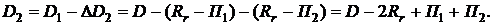(2.38)

Сумма процентов П_k, выплачиваемых за пользование кредитом при k-м платеже, и задолженность по кредиту после k-го платежа D_k определяются формулами

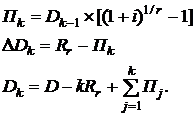(2.39)

Общее число платежей в погашение кредита равно nr. Размер последнего платежа R_nr должен полностью погасить задолженность по кредиту и проценты за пользование кредитом.

Задолженность по телу кредита перед последним платежом будет равна

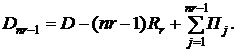(2.40)

Проценты по кредиту П_nr и размер последнего платежа определяются формулами

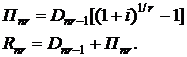(2.41)

В результате проведенных расчетов общая сумма уплаченных процентов за пользование кредитом будет равна

,

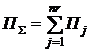и должны соблюдаться следующие равенства

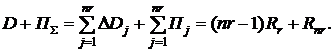(2.42)

Проведем расчет графика платежей в погашение кредита на конкретном примере.

Пример 2.1. В коммерческом банке взят потребительский кредит на сумму 100 тыс. руб. сроком на один год (n = 1) под 20 % годовых (i = 0,2). Погашение кредита осуществляется четырьмя (r = 4) ежеквартальными платежами. Рассчитать график платежей в погашение кредита.

Решение. По формуле (2.33) определяем размер разового квартального платежа

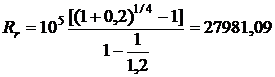руб.

По формулам (2.34), (2.35) и (2.36) рассчитываем суммы выплачиваемые в погашение процентов по кредиту П₁, тела кредита 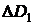и задолженность по кредиту после первого платежа

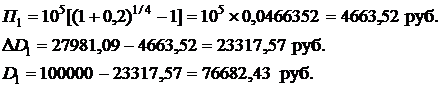
По формулам (2.39) рассчитываем аналогичные параметры графика платежей при k = 2 и 3.

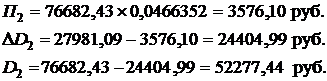
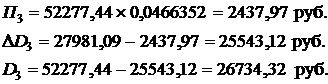
Для последнего четвертого платежа параметры графика платежей по кредиту рассчитываем по формулам (2.40):

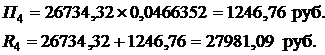
Результаты расчета графика платежей сведены в табл. 2.1.

Приведенные выше формулы и расчеты справедливы, когда банк рассчитывает доходность по кредиту по схеме сложных процентов.

Таблица 2.1

№ платежа	Размер платежа, руб.	Погашение кредита, руб.	Проценты за кредит, руб.	Текущая задолженность по кредиту, руб.
	27981,09	23317,57	4663,52	76682,43
	27981,09	24404,99	3576,10	52277,44
	27981,09	25543,12	2437,97	26734,32
	27981,09	26734,32	1246,76
Итого	111924,36		11924,36

Пример 2.1а. Для сравнения приведем результаты расчетов графика платежей, когда процентные доходы по кредиту банк рассчитывает не по формуле (2.34), а по процентной ставке i_r, пересчитанной к временному интервалу между платежами

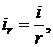(2.43)

где i – годовая процентная ставка;

r – количество платежей в году.

В этом случае для расчета размера разовых платежей нужно использовать формулу (2.6):

(2.44)

Проведем расчет графика платежей по кредиту при ставке доходности, определяемой формулой (2.43), для условий кредитования, указанных в рассматриваемом примере.

Определим размер разовых платежей

Определяем сумму процентов П₁, уплачиваемых за пользование кредитом, и сумму 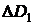, выплачиваемую в погашение тела кредита при первом платеже

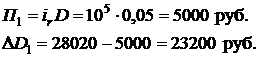
Сумма задолженности по кредиту после первого платежа будет равна

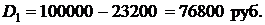
Рассчитываем суммы П_к, ∆D_k и D_k на втором k = 2 и третьем k = 3 платеже

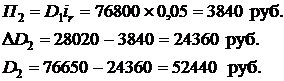
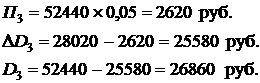
При четвертом платеж процентные доходы банка составят

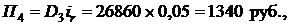
а размер четвертого платежа будет равен

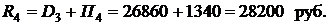
Результаты расчетов приведены в табл. 2.1 (под диагональной чертой). Из сравнения результатов расчета видно, что для банка выгоднее, когда процентные доходы банка начисляются по ставке, определяющейся формулой (2.43). Банковская методика расчета графика платежей по кредиту совпадает с методикой, приведенной в примере 2.1.

Валютные кредиты

Рассмотрим возможные схемы валютных операций при кредитовании и погашении кредитов. Первая схема, имеющая печальные последствия на рубеже 2014-2015 годов, характерна для ипотечного кредитования.

I. Потенциальному ссудозаемщику необходима некоторая сумма в рублях D_R. Для получения ссудозаемщик решил взять кредит в иностранной валюте под годовую процентную ставку j_B на сумму 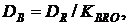где 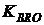- обменный курс валюты в рубли на момент заключения кредитного договора. Погашение кредита осуществляется постоянными платежами r раз в год в валюте кредита R_B. Ссудозаемщик имеет только рублевые доходы, и погашение валютных платежей он осуществляет за счет рублевых доходов, конвертируя их в валюту по обменному курсу 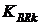на очередной k-й момент оплаты кредита.

Результаты данной финансовой операции целесообразно сравнивать с примером, рассмотренным в п. 2.4 при рублевом кредитовании.

Для сопоставимости результатов кредитования по данной схеме и с примером, рассмотренным в п. 2.4, примем следующие условия предоставления валютного кредита.

Размер валютного кредита D_В определяется из условия эквивалентности его 100 тыс. руб. на момент заключения кредитного договора при курсе обмена валюты в рубли 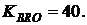Кредитный договор заключается на один год под годовую процентную ставку j_B = 8 % годовых. Погашение кредита осуществляется четырьмя ежеквартальными платежами r = 4. Будем считать, что обменный курс валюты за срок кредитного договора изменяется линейно (рис. 2.5)

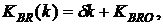(2.45)

где 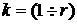- номер очередного платежа в погашение валютного кредита;

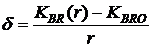- скорость нарастания или убывания обменного курса валюты.

Расчеты для приведенных выше условий дают следующие результаты:

1) Размер валютного кредита

?.

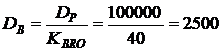2) Для упрощения расчетов размер ежеквартальных платежей будем определять по методике, рассмотренной в примере 2.1а.

?.

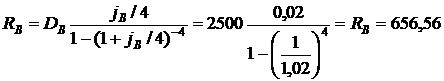3) Размер ежеквартальных платежей в российских рублях, при скорости нарастания обменного курса валюты 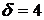руб./квартал

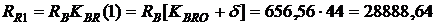руб.

руб.

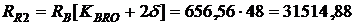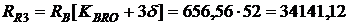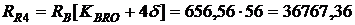руб.

руб.

4) Общая сумма в рублях, затраченная на погашение валютного кредита

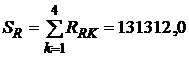руб.

5) Общая сумма в рублях, затраченная на погашение кредита 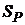, имеет линейную зависимость от δ

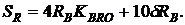
6) Построим график зависимости 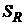от δ. Для этого рассчитаем 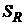при δ = 0

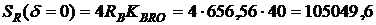руб.

Зависимость 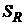от δ приведена на рис. 2.5. На этом же рисунке отмечена сумма, уплаченная в погашение рублевого кредита D = 100 тыс. руб. 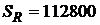руб. (см. табл. 2.1).

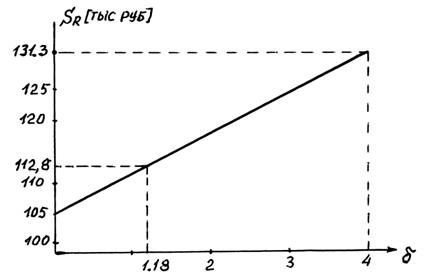
Рис. 2.5. Зависимость 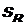от δ

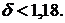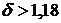Из рис. 2.5 можно сделать следующий вывод. При линейном нарастании обменного курса валюты (2.45) за срок кредитования валютный кредит оказывается выгоднее при скорости изменения обменного курса валюты При рублевая сумма, уплаченная в погашение валютного кредита 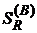(рис. 2.5), оказывается больше 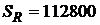руб. суммы, уплаченной в погашение рублевого кредита.

Рассмотрим другие схемы валютного кредитования.

II. Потенциальный ссудозаемщик осуществляет внешнеэкономическую деятельность, от которой получает валютные доходы. Для продолжения ВЭД ссудозаемщику нужен кредит в размере 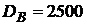?. Эта сумма может быть получена:

а) непосредственно в валюте под ставку валютного кредита 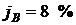годовых;

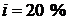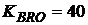б) по рублевому кредиту по ставке годовых при сумме рублевого кредита и курсе обмена валюты руб.

В обоих случаях срок кредитования один год, кредит гасится ежеквартальными платежами из валютных доходов ссудозаемщика.

Определить, какой из видов кредитования (Пример 2.1 или Пример 2.1а) выгоднее при линейном изменении обменного курса валюты за срок кредитования. Размер разового валютного платежа можно рассчитать по формулам (2.33) или (2.44).

Рассчитаем размер ежеквартальных платежей при кредитовании по схеме апо формуле (2.44)

?.

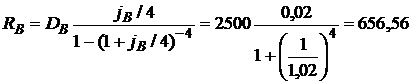Рассчитаем данные по ежеквартальным платежам

1-й платеж ?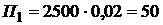

?

?

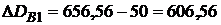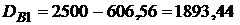2-й платеж ?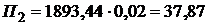

?

?

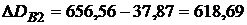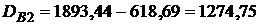3-й платеж ?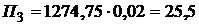

?

?

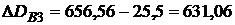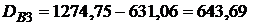4-й платеж ?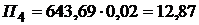

?

?

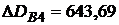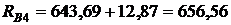Суммарные валютные выплаты в погашение валютного кредита составят

?.

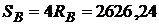То есть переплата по кредиту будет равна

?,

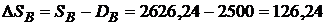и эффективная процентная ставка по кредиту составляет

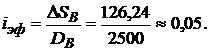
Рассчитаем график платежей 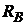, вносимых из валютных доходов в погашение рублевого кредита (Пример 2.1а).

Рассчитаем размер необходимого рублевого кредита

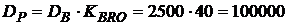руб.

Рассчитываем размер ежеквартальных платежей R_R

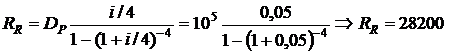руб.

Расчет графика платежей по данному кредиту приведен а табл. 2.1.

Так как рублевый кредит гасится из валютных доходов, рассчитаем сумму ежеквартальных выплат в валюте с учетом формулы (2.45) при 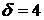руб./квартал:

?

?

?

?.

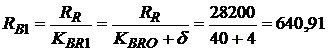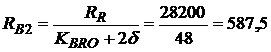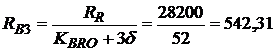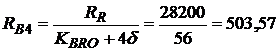Суммарные валютные выплаты на погашение рублевого кредита составят ?.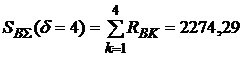

Аналогичным образом рассчитаем суммарные валютные выплаты 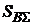на погашение рублевого кредита при других значениях 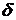и построим график зависимости 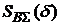(рис. 2.6).

На рис. 2.6 отмечено также значение суммарных валютных выплат по погашению валютного кредита 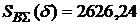?. Из графика видно, что при 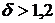выгоднее оказывается получение кредита по схеме "б", а при 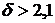суммарные валютные выплаты по рублевому кредиту оказываются меньше, чем валютный размер кредита ?.

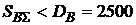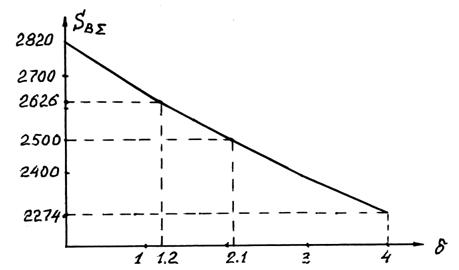
Рис. 2.6. График зависимости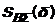

2.6. Годовая и срочная ренты при m-кратном начислении процентов

Для годовой ренты постнумерандо при m-кратном начислении сложных процентов формулу (2.4) для современной стоимости ренты можно записать в виде

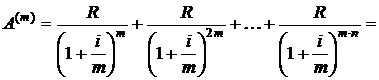
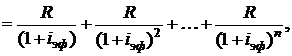
где i_эф – определяется формулой (1.11).

Данная сумма является геометрической прогрессией с первым членом 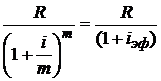и знаменателем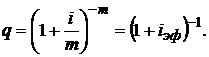

Отсюда для современной стоимости годовой ренты с m-кратным начислением процентов по аналогии с формулой (2.6) получим

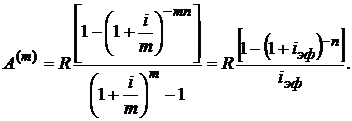(2.46)

Из сравнения формул (2.46) и (2.6) видно, что формула (2.46) получается из формулы (2.6) путем замены в ней годовой процентной ставки i на эффективную годовую процентную ставку i_эф при m-кратном начислении процентов (1.11). Коэффициент приведения для данной ренты будет равен

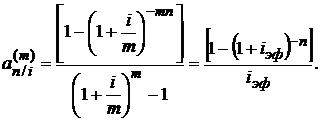(2.47)

Аналогично для конечной стоимости годовой ренты с m-кратным начислением процентов и коэффициента наращения можно получить формулы

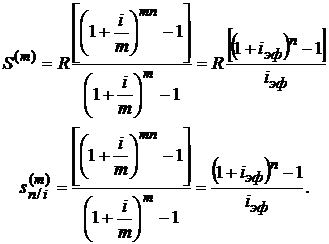(2.48)

Для ренты пренумерандо с m-кратным начислением процентов справедливы формулы

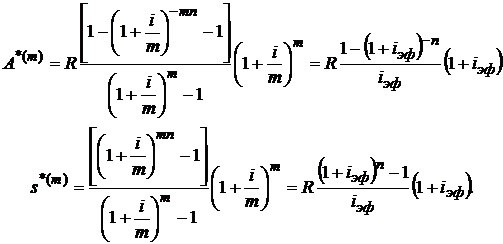(2.49)

Для современной и конечной стоимости r-срочной ренты постнумерандо с m-кратным начислением процентов можно получить формулы

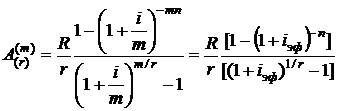
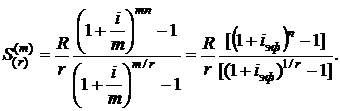(2.50)

При m = r формулы (2.50) преобразуются к виду

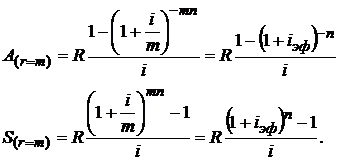(2.51)

При вычислении современной и конечной стоимостей ренты пренумерандо формулы (2.50) и (2.51) необходимо умножить на .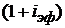

Арифметическая рента

В арифметической ренте величина периодических платежей представляет собой арифметическую прогрессию. Поток платежей арифметической ренты постнумерандо можно записать в виде

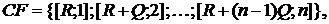
где Q – разность арифметической прогрессии. Величина Q характеризует, насколько каждый последующий платеж отличается от предыдущего.

При Q > 0 арифметическая прогрессия будет возрастающей, при Q < 0 – убывающей.

Определим современную А и конечную, наращенную S стоимости арифметической ренты.

Приведенная современная стоимость арифметической ренты определяется суммой:

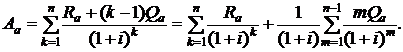(2.52)

Первая сумма в формуле (2.52) определяется формулой (2.6). Вторая сумма в (2.52) может быть записана в виде

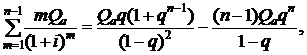(2.53)

где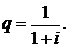

Вторая сумма в формуле (2.52) может быть преобразована к виду

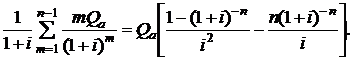(2.54)

С учетом формул (2.6) и (2.54) современная стоимость арифметической ренты постнумерандо определится формулой

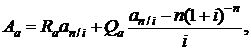(2.55)

где коэффициент приведения 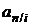определяется формулой (2.7).

На рис. 2.7 приведен график зависимости современной стоимости арифметической ренты от отношения 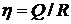для двух значений процентной ставки дисконтирования i и при n = 4.

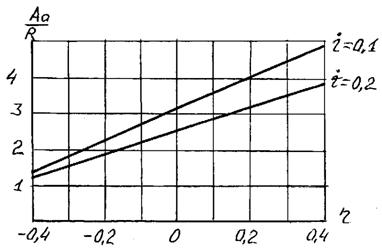
Рис. 2.7

Конечная наращенная стоимость арифметической ренты определяется суммой

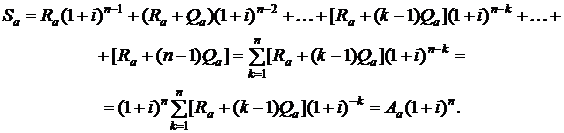
С учетом формулы (2.55) для конечной стоимости арифметической ренты получим

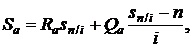(2.56)

где коэффициент наращения 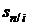определяется формулой (2.9).

Для современной и конечной стоимостей арифметической ренты пренумерандо аналогично формулам (2.18) и (2.19) можно записать:

Для r-срочной арифметической ренты постнумерандо поток платежей показан на рис. 2.4, в котором размер k-го платежа равен 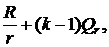а количество платежей равно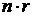 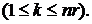Современная стоимость r-срочной арифметической ренты определится суммой

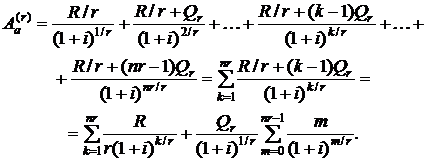(2.57)

Первая сумма в формуле (2.57) является убывающей геометрической прогрессией со знаменателем 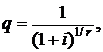первым членом 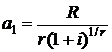и определяется формулой (2.21).

Вторая сумма является арифметико-геометрической прогрессией со знаменателем 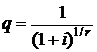и в соответствии с формулой (2.53) может быть преобразована к виду:

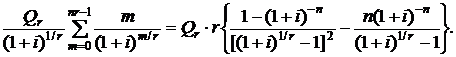(2.58)

В соответствии с формулами (2.21) и (2.58) для современной стоимости арифметической ренты постнумерандо получим формулу

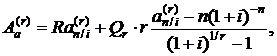(2.59)

где коэффициент приведения 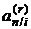определяется формулой (2.22).

Конечная, наращенная стоимость r-срочной арифметической ренты постнумерандо определится формулой

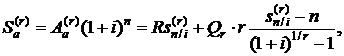(2.60)

где коэффициент приведения 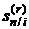определяется формулой (2.24).

Геометрическая рента

Геометрической называется рента, в которой каждый последующий платеж отличается в 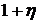раз от предыдущего, т. е.

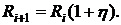
Поток платежей такой ренты постнумерандо можно записать в виде

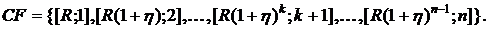
Размеры платежей в данном потоке представляют собой геометрическую прогрессию со знаменателем 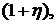а параметр 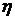является темпом прироста платежей, он определяет процентную долю, на которую отличается каждый последующий платеж от предыдущего.

Современная стоимость такой ренты равна сумме диконтированных платежей

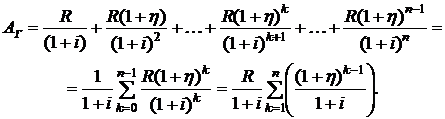(2.61)

Современная стоимость 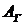является суммой членов геометрической прогрессии со знаменателем 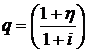и первым членом 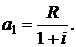С учетом формулы (2.5) для современной стоимости геометрической ренты постнумерандо получим

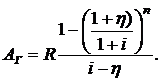(2.62)

Формула (2.62) может использоваться только 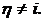при При 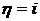формула (2.61) преобразуется к виду

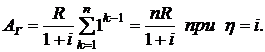(2.63)

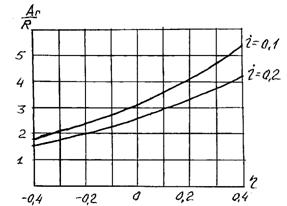
Рис. 2.8

На рис. 2.8 приведена зависимость современной стоимости геометрической ренты от темпа прироста платежей 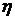при двух значениях процентной ставки дисконтирования i и n = 4.

Конечная наращенная стоимость геометрической ренты постнумерандо определяется суммой

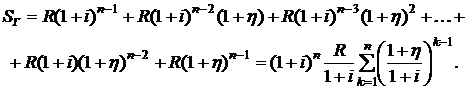
Сравнивая данную формулу с (2.61), для конечной стоимости геометрической ренты получим

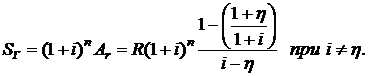(2.64)

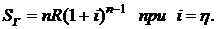
Для r-срочной геометрической ренты постнумерандо финансовый поток состоит из 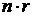платежей, образующих геометрическую прогрессию с первым членом 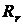и знаменателем 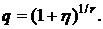Современная стоимость такой ренты равна сумме дисконтированных платежей с коэффициентом дисконтирования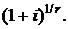

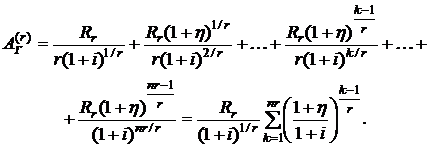(2.65)

Данная сумма является суммой nr членов геометрической прогрессии с первым членом 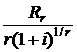и знаменателем 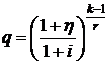и в соответствии с формулой (2.5) может быть записана в виде

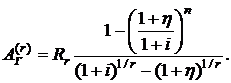(2.66)

Конечная наращенная стоимость геометрической r-срочной ренты постнумерандо может быть получена умножением современной стоимости 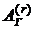на множитель наращения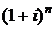

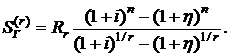(2.67)

Современная 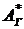и конечная 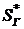стоимости геометрической ренты пренумерандо могут быть получены умножением формул (2.62) и (2.64) на множитель (1 + i).