Тема 1. Введение в теорию игр
Принятие решений в условиях риска и неопределенности.
Игра как математическая модель принятия решения в условиях противоположности интересов.
Основные понятия и определения теории игр. Классификация игр.
Применение теории игр в различных областях науки и практики.
Тема 2.Антагонистические игры. Решение игр в чистых стратегиях
Антагонистическая игра как математическая модель принятия решения в условиях противоположности интересов.
Матрица выигрышей (платежная матрица, матрица игры). Мажорирование (доминирование, дублирование) стратегий, аффинное преобразование матрицы выигрышей.
Нижняя и верхняя цена игры.Максиминные и минимаксные стратегии.Чистые стратегии игроков. Седловая точка игры. Цена игры в чистых стратегиях.
Тема 3. Решение игр в смешанных стратегиях
Смешанные стратегии. Нижняя и верхняя цена игры в смешанных стратегиях. Основная теорема теории игр Дж. Фон Неймана.
Геометрическая интерпретация множества смешанных стратегий. Активные стратегии.Определение функции выигрыша в смешанных стратегиях и формулы ее представления.
Аналитическое и геометрическое решение игр 2´2, 2´n, m´2. Алгоритмы решений.
Тема 4. Взаимосвязь матричных игр и задач линейного программирования
Взаимно двойственные задачи линейного программирования. Теоремы двойственности.
Приведение антагонистической игры к паре взаимно двойственных стандартных задач линейного программирования. Формулы перехода от решения взаимно двойственных задач линейного программирования к цене игры и смешанным стратегиям игроков.
Решение антагонистических игр с помощью надстройки «Поиск решения» табличного процессора Excel.
Тема 5. Игры с природой
Понятие игры с природой.Природаи ее состояния. Матрицавыигрышей. Матрица рисков и ее свойства. Оптимальные стратегии по Парето.
Принятие решений в условиях неопределенности.КритерийВальда, максимаксный критерий, критерий Гурвица, критерий Сэвиджа, критерий максимизации среднего ожидаемого дохода, критерий равновероятности Лапласа, критерий Байеса-Лапласа.
5.2. Учебно-тематический план
Общая трудоёмкость дисциплины составляет 3 зачётные единицы.
Вид промежуточной аттестации – зачет.
| № п/п | Наименование темы (раздела) дисциплины | Трудоёмкость в часах | Формы текущего контроля успевае-мости | |||||
| Всего часов | Аудиторная работа | Самостоя-тельная работа | ||||||
| Общая | Лек-ции | Прак-тиче-ские и семи-нарс-кие заня-тия | Занятия в интерак-тивных формах | |||||
| Тема 1. Введение в теорию игр | 17/17 | 4/0 | 2/0 | 2/0 | 1/0 | 13/17 | Самос-тоя-тельные работы Участие в решении задач на практи-ческих занятиях. Собесе-дования по домаш-ним заданиям Конт-рольная работа | |
| Тема 2. Антагонистические игры. Решение игр в чистых стратегиях | 22/21 | 8/2 | 4/0 | 4/2 | 1/1 | 14/19 | ||
| Тема 3. Решение игр в смешанных стратегиях | 23/23 | 8/3 | 4/1 | 4/2 | 2/1 | 15/20 | ||
| Тема 4. Взаимосвязь матричных игр и задач линейного программирования | 22/22 | 8/3 | 4/1 | 4/2 | 2/1 | 14/19 | ||
| Тема 5. Игры с природой | 24/25 | 8/2 | 4/0 | 4/2 | 2/1 | 16/23 | ||
| Итого: | 108/108 | 36/10 | 18/2 | 18/8 | 8/4 | 72/98 |
Содержание практических и семинарских занятий
| Наименование темы дисциплины | Тематика практических и семинарских занятий | Содержание и формы проведения практических и семинарских занятий |
| Тема 1. Введение в теорию игр | Игра как математическая модель принятия решения в условиях противоположности интересов | Содержание занятия:Принятие решений в условиях риска и неопределенности. Основные понятия и определения теории игр. Классификация игр. Применение теории игр в различных областях науки и практики. Форма занятия: доклады, групповое обсуждение, дискуссия. Интерактив –50%/- от трудоемкости семинарского занятия:доклады студентов по результатам проектной деятельности по темам: 1. История зарождения и развития теории игр; 2. Основные понятия и определения теории игр. Классификация игр. 3. Применение теории игр в различных областях науки и практики. Вопросы для самостоятельной работы студентов: 1. В чем состоит различие между реальным конфликтом и игрой? 2. Что общего и в чем различие понятий: риск и неопределенность? 3. Сделайте предположение о том, что может представлять собой математическая модель игры. Рекомендуемые источники:[8.1], [8.2],[8.5] |
| Тема 2. Антагонистические игры. Решение игр в чистых стратегиях | Решение игр в чистых стратегиях | Содержание занятия: Матрица выигрышей (платежная матрица, матрица игры). Мажорирование (доминирование, дублирование) стратегий, аффинное преобразование матрицы выигрышей. Нижняя и верхняя цена игры. Максиминные и минимаксные стратегии. Чистые стратегии игроков. Седловая точка игры. Цена игры в чистых стратегиях. Форма занятия:решение задач, разбор конкретных ситуаций. Интерактив –25%/50% от трудоемкости семинарского занятия: разбор конкретных ситуаций. Вопросы для самостоятельной работы студентов: 1. Почему в матричной игре в качестве платежной матрицы принимается матрица выигрышей игрокаА? 3. В чем состоит суть максиминного принципа оптимальности и как называется выигрыш, полученный в соответствии с этим принципом? 4. В чем состоит польза свойства равнозначности седловых точек при ихнахождении? 5. Как связаны между собой цена игры и существование седловых точек? Рекомендуемые источники:[8.1], [8.2],[8.3],[8.5] |
| Тема 3. Решение игр в смешанных стратегиях | Решение игр в смешанных стратегияхграфо-аналитическим методом | Содержание занятия:Смешанные стратегии. Нижняя и верхняя цена игры в смешанных стратегиях. Основная теорема теории игр Дж. Фон Неймана. Геометрическая интерпретация множества смешанных стратегий. Активные стратегии. Определение функции выигрыша в смешанных стратегиях и формулы ее представления. Аналитическое и геометрическое решение игр 2´2, 2´n, m´2. Алгоритмы решений. Форма занятия:решение задач, разбор конкретных ситуаций. Интерактив –50%/50% от трудоемкости семинарского занятия: разбор конкретных ситуаций. Вопросы для самостоятельной работы студентов: 1. Почему сумма вероятностей применения игроком чистых стратегий в смешанной стратегии равна единице? 2. Дайте геометрическую интерпретацию множества всех смешанных стратегий для случаев: m =1; m = 2; m = 3. 3.Почему игра в смешанных стратегиях называется смешанным расширением игры в чистых стратегиях? 4. Какова связь между ценами игры в чистых и в смешанных стратегиях? 5. Каковы физические механизмы применения смешанных стратегий? Рекомендуемые источники: [8.2],[8.3],[8.5] |
| Тема 4. Взаимосвязь матричных игр и задач линейного программирования | Решение матричных игр методами линейного программирования | Содержание занятия:Приведение антагонистической игры к паре взаимно двойственных стандартных задач линейного программирования. Формулы перехода от решения взаимно двойственных задач линейного программирования к цене игры и смешанным стратегиям игроков. Решение антагонистических игр с помощью надстройки «Поиск решения» табличного процессора Excel. Форма занятия:решение задач, разбор конкретных ситуаций. Интерактив –50%/50% от трудоемкости семинарского занятия: разбор конкретных ситуаций. Вопросы для самостоятельной работы студентов: 1. Каким образом цена игры и оптимальные смешанные стратегии игроков определяются по оптимальным решениям пары двойственных друг другу стандартных задач линейного программирования? 2. Каким образом по цене игры размера[m×n] и оптимальным смешанным стратегиям обоих игроков можно определить оптимальные решения пары двойственных задач линейного программирования? 3. Как определяется риск неполучения максимального выигрыша при выборе смешенной стратегии? Рекомендуемые источники: [8.2], [8.3],[8.5] |
| Тема 5. Игры с природой | Методы решения игр с природой | Содержание занятия:Матрица выигрышей в игре с природой. Матрица рисков и ее свойства. Оптимальные стратегии по Парето. Принятие решений в условиях неопределенности. Критерий Вальда, максимаксный критерий, критерий Гурвица, критерий Сэвиджа, критерий максимизации среднего ожидаемого дохода, критерий равновероятности Лапласа, критерий Байеса-Лапласа. Форма занятия:решение задач, разбор конкретных ситуаций. Интерактив –50%/50% от трудоемкости семинарского занятия: разбор конкретных ситуаций. Вопросы для самостоятельной работы студентов: 1. Чем характеризуется ситуация принятия решений, о которой говорят «принятие решений в условиях риска»? 2. Перечислите черты, характеризующие игры с природой. 3. Что представляет собой область определения и множество значений выигрыш-функции в игре с природой? 4. Какого вида неопределенности могут встретиться при принятии решений? 5. Объясните, почему критерий Сэвиджа является крайне пессимистическим. Рекомендуемые источники:[8.1], [8.2], [8.3], |
6. Учебно-методическое обеспечение для самостоятельной работы обучающихся по дисциплине
6.1. Формы внеаудиторной самостоятельной работы
| Наименование разделов, тем, входящих в дисциплину | Формы внеаудиторной самостоятельной работы | Трудоемкость в часах | Указание разделов и тем, отводимых на самостоятельное освоение обучающимися | ||
| Тема 1. Введение в теорию игр | Работа с учебной литературой, подготовка к семинарским и практическим занятиям. | 13/17 |
| ||
| Тема 2. Антагонистические игры. Решение игр в чистых стратегиях | Работа с учебной литературой, подготовка к семинарским и практическим занятиям, решение задач. Выполнение заданий домашней контрольной работы. | 14/19 | Принцип доминирования. Аффинное преобразование матрицы игры. | ||
| Тема 3. Решение игр в смешанных стратегиях | Работа с учебной литературой, подготовка к семинарским и практическим занятиям, решение задач. | 15/20 | Геометрическая интерпретация множества смешанных стратегий. Активные стратегии. | ||
| Тема 4. Взаимосвязь матричных игр и задач линейного программирования | Работа с учебной литературой, подготовка к семинарским и практическим занятиям, решение задач. | 14/19 | Взаимно двойственные задачи линейного программирования. Теоремы двойственности.
| ||
| Тема 5. Игры с природой | Работа с учебной литературой, подготовка к семинарским и практическим занятиям, решение задач. Выполнение заданий домашней контрольной работы. | 16/23 | Подбор реальных ситуаций, для которых модель «Игра с природой» является подходящей. Понятие о статистических играх. Оптимальные стратегии по Парето. Критерий Байеса-Лапласа. | ||
| ИТОГО | - | 72/98 | - |
6.2. Методическое обеспечение для аудиторной и внеаудиторной самостоятельной работы
Пример контрольной работы
Задание 1. С учетом вариантов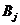 
сложившегося на рынке поведения покупателей в микрорайоне города коммерческое предприятие разработало несколько технологий продажи товаров 
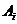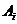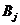. Возможные варианты среднедневного товарооборота (в млн руб.) в зависимости от различных сочетаний и приведены в матрицах:
Матрица 1
| Игроки | В1 | В2 | В3 | В4 |
| А1 | 12 + t | 20 + v | 15 + u | 12 + t |
| А2 | 12 + t | 15 + u | 7 + v | 3 + u |
| А3 | 3 + u | 3 + u | 12 + t | 15 + u |
| А4 | s | 20 + v | 7 + v | 7 + v |
Матрица 2
| Игроки | В1 | В2 | В3 | В4 |
| А1 | 4 + v | 8 + t | s | 11 + u |
| А2 | s | 4 + v | 16 + v | 11 + u |
| А3 | 4 + v | 8 + t | 11 + u | s |
| А4 | 11 + u | 4 + v | 4 + v | 4 + v |
Матрица 3
| Игроки | В1 | В2 | В3 | В4 | B5 |
| А1 | u + 2 | v + 6 | u + 2 | t + 10 | v + 17 |
| А2 | t – 2 | v + 17 | t – 2 | u + 14 | v + 6 |
| А3 | s – 6 | v + 6 | t – 2 | u + 2 | v + 6 |
| А4 | u + 2 | v + 6 | u + 2 | t + 10 | t + 10 |
Значения параметров, входящих в матрицы:
| № варианта | s | t | u | v |
Требуется:
1) Определить верхние и нижние значения товарооборота коммерческого предприятия.
2) Найти седловую точку игры, если она есть. Используя оптимальные чистые стратегии и чистую цену игры, сделайте выводы экономического характера.
Задание 2.Найти оптимальную смешанную стратегию руководителя коммерческого предприятия (игрок А) и гарантированный средний выигрыш при выборе из двух новых технологий продажи товаров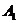 
и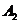 
, если известны выигрыши каждого вида продажи по сравнению со старой технологией (игрок В), которые представлены в виде матрицы:
| Игрок А | Игрок В | |
| B1 | B2 | |
| A1 | a11 | a12 |
| A2 | a21 | a22 |
Элементы матрицы заданы в таблице:
| № варианта | а11 | а12 | а21 | а22 |
Задание 3.Найти решения матричных игр графоаналитическим методом.
А)Сельскохозяйственное предприятие имеет возможность выращивать две культуры. Прибыль предприятия от реализации выращенной культуры зависит от объема полученного урожая. Урожай первой культуры выше при сухой погоде, а второй выше при более влажной. Состояние погоды в летний период можно рассматривать как следующие стратегии природы (игрок В):
1) 
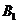– лето жаркое сухое;
2) 
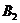– лето жаркое влажное;
3) 
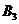– лето теплое влажное;
4) 
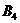– лето теплое сухое;
5) 
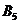– лето прохладное.
Стратегии предприятия (игрок А):
1) 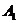– выращивать первую культуру;
2) 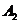– выращивать вторую культуру.
Расчеты прибыли предприятия (в млн руб.) в зависимости от состояния погоды приведены в матрицах, соответствующих каждому варианту:
| Варианты | Стратегии игрокаА | Стратегии игрокаВ | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 | ||||||
| А1 | ||||||
| А2 |
Требуется определить оптимальные стратегии поведения сельскохозяйственного предприятия и его гарантированный выигрыш.
В)Сельскохозяйственное предприятие (игрок А) должно выращивать определенную культуру, например картофель, на отведенном для этой цели участке. Урожайность картофеля зависит от количества внесенных удобрений и от состояния погоды. Рассматриваются два возможных характера погоды (игрок В):
1) 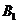– лето сухое;
2) 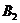– лето влажное.
Возможные варианты внесения удобрений:
1) 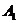– количество удобрений на 1 га соответствует определенной норме (норму принять равной 1);
2) 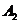– количество удобрений на 30 % выше нормы;
3) 
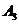– количество удобрений на 40 % ниже нормы;
4) 
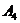– количество удобрений на 5 % ниже нормы.
Предприятие произвело расчет прибыли в зависимости от возможных стратегий своих и природы. Матрицы прибылей для различных вариантов задачи представлены в таблице:
| ИгрокА | Номер варианта | |||||||||||||||||||
| ИгрокВ | ||||||||||||||||||||
| В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | В1 | В2 | |
| А1 | ||||||||||||||||||||
| А2 | ||||||||||||||||||||
| А3 | ||||||||||||||||||||
| А4 |
Требуется определить оптимальное количество внесения удобрений и гарантированную прибыль предприятия при любой погоде.
Задание 4.Дана матрица последствий Q, в которой строки – возможные управленческие решения, а столбцы – исходы, соответствующие альтернативным вариантам реальной ситуации (состояниям внешней среды).
Необходимо:
1. Определить множество оптимальности по Парето.
2. Выбрать рациональную управленческую стратегию в ситуации неопределенности и риска, применяя критерии Вальда, максимакса, Сэвиджа, Гурвица, приняв рекомендуемое для критерия Гурвица значение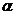 
, правило максимизации среднего ожидаемого дохода.
Вариант 1.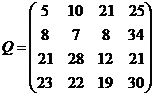 
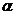; =0,75