Модель равномерного распределения при оценке риска потерь

Закону равномерного распределения вероятностей соответствует следующая формула определения вероятности потерь:

где b - верхняя граница зоны риска;

a - нижняя граница зоны риска,

x - фактическое значение КТЛ.

Пример 2.10.

Предстоит заключение сделки с предприятием о поставке ему продукции на крупную сумму. Согласно бухгалтерским данным фактическое значение КТЛ у этого предприятия равно 1,6. Определить вероятность того, предприятие окажется неплатежеспособным и не сможет расплатиться за поставленную ему продукцию.

Решение.

Статистики неплатежеспособности и банкротств поставщик не имеет, поэтому придется взять границы зоны риска на следующем уровне a=1 и b=2. Отсюда вероятность того, поставщик может понести потери, равна:

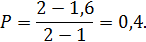
Допущение о существовании закона равномерного распределения вероятностей банкротств является в определенной мере произвольным. Но когда нет никаких данных, то приходится идти и на такое допущение.

Противоположным понятию риска потерь является понятие надежности. Вероятность того, что партнер окажется надежным и не подведет:

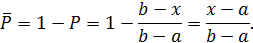
Так, при риске потерь в 40% надежность партнера будет равна:

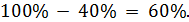
Уточнение границ зоны неопределенности для коэффициента

Текущей ликвидности

Выше рассматривались возможности леммы Маркова, неравенства Чебышева и модели равномерного распределения для целей уточнения уровня риска. Во всех случаях в этом рассмотрении участвовал коэффициент текущей ликвидности - КТЛ.

Во всех случаях возникала необходимость определения границ зоны неопределенности для этого показателя. Считается, что КТЛ у благополучного предприятия должен быть не менее 2. Это объясняется тем, что:

1) часть активов может утратить свою стоимость (например, ценные бумаги);

2) часть активов может не найти спроса, и деньги от их реализации не удастся использовать на погашение долгов (например, материалы и продукция, не являющиеся товарами массового спроса);

3) часть активов может пропасть (например, признанная безнадежной дебиторская задолженность).

Поэтому при равенстве активов долгам всегда будет существовать риск невыполнения предприятием своих обязательств перед кредиторами или инвесторами. Для гарантированного выполнения этих обязательств от предприятий требуется иметь активов в два раза больше, чем долгов.

Тогда можно сказать, что предприятия с КТЛ менее единицы являются банкротами: их активов заведомо не хватит на погашение их долгов.

В промежутке между этими двумя значения лежит зона неопределенности. У предприятий со значениями КТЛ в пределах от 1 до 2 судьба неясна: они могут стать, а могут и не стать банкротами. Их нельзя назвать благополучными, но и нельзя считать состоявшимися банкротами, поскольку они могут вернуть (а могут и не вернуть) кредиты или вложенные в них средства. Инвестиции в них сопряжены с риском потерь: вероятность потерь тем выше, чем ближе их КТЛ к значению 1.

Выдвигаются разные предложения по уточнению границ зоны неопределенности. Например, предлагается применение дискриминантного анализа, проведение которого по прошлым обследованиям предприятий позволяет разделить их на две группы (банкроты/ не банкроты), а также сделать выводы о возможном поведении новых предприятий с соответствующим значением КТЛ. Результаты дискриминантного анализа представлены в таблице 2.3.

Таблица 2.3

Распределение предприятий по величине КТЛ на группы

надежных и ненадежных

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью
Предприятия, утратившие платежеспособность

По этой таблице, при 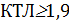банкротство полностью исключается, а при значении 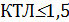исключается возможность восстановления платежеспособности.

Тогда, зона риска (или неопределенности) имеет границы: 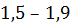. В таком случае вероятность потери инвестиций, вложенных в предприятия с КТЛ=1,6, будет равна:

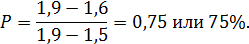
Пример 2.11.

Среди клиентов коммерческого банка имеется 5 должников, утративших в силу ряда обстоятельств платежеспособность и более года не возвращающих взятые у банка краткосрочные ссуды. Среднее значение отношения оборотных активов к краткосрочной задолженности, именуемое коэффициентом текущей ликвидности (КТЛ), исчисленное по бухгалтерским балансам за ряд отчетных периодов, составило у них соответственно: 1,2; 1,3; 1,4; 1,5 и 1,6.

Платежеспособным предприятием, у которого не возникает проблем с погашением долгов, принято считать такое, у которого КТЛ находится на уровне не ниже 2. Используя лемму Маркова, найти вероятности того, что должники не смогут довести КТЛ до двух и не вернут свои долги банку.

Решение.

Клиент останется неплатежеспособным и не вернет долг, если его КТЛ не превысит значение 2. Вероятность этого можно определить по формуле:

.

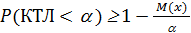При a = 2 вероятности невозврата долгов как минимум равны:

№ предприятия	Среднее значение КТЛ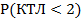
	1,2	0,4
	1,3	0,35
	1,4	0,3
	1,5	0,25
	1,6	0,2

Пример 2.12.

Коммерческий банк ведет статистику просрочки и невозврата ссуд, согласно которой достаточная гарантия платежеспособности имеется только у тех клиентов, где КТЛ оказывается на уровне не менее 2,5. Это объясняется тем, что банк ведет дела с клиентами, активы которых не всегда бывают достаточно высокого качества: активы не всегда можно быстро и без потерь продать, чтобы погасить за вырученные от этой продажи средства долги. Поэтому нормативное двукратное превышение активов над долгами в данном случае оказывается недостаточным.

Уточните с учетом вышесказанного вероятности потерь банка на операциях с клиентами из примера 2.9.

Решение.

При a = 2,5 вероятности невозврата долгов как минимум равны:

№ предприятия	Среднее значение КТЛ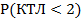
	1,2	0,52
	1,3	0,48
	1,4	0,44
	1,5	0,40
	1,6	0,36

Пример 2.13.

Среди дебиторов фирмы имеется должник с большой просрочкой платежа по своему долгу. Эксперты фирмы смогли получить о финансовом положении этого должника только очень ограниченную информацию: о величине коэффициента текущей ликвидности (КТЛ) за последние три месяца. Они приведены в таблице.

Месяц
Значение КТЛ	1,6	1,5	1,4

Определите вероятность того, что:

1) должник сможет восстановить свою платежеспособность, подняв КТЛ до уровня не менее 2;

2) данный долг придется списать как безнадежный.

Используйте при решении лемму Маркова и неравенство Чебышева, сопоставьте полученные с их помощью результаты.

Решение.

Среднее значение КТЛ:

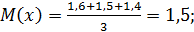
а дисперсия равна:

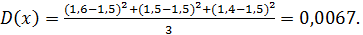
По лемме Маркова вероятность восстановления платежеспособности составит не более:

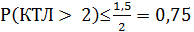, или не более 75%,

а вероятность потери долга будет равна как минимум 25%

По неравенству Чебышева принимаем .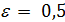

Вероятность восстановления платежеспособности равна не более:

а) находим вероятность отклонения от 1,5 на 0,5 в обе стороны:

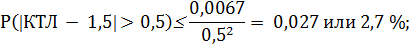
б) вероятность отклонения в одну сторону 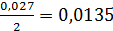или приблизительно 1,4%.

Вероятность потери долга равна не менее .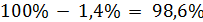

Пример 2.14.

На основании собранных статистических данных было установлено, что у предприятий, имеющих устойчивую платежеспособность коэффициент текущей ликвидности (КТЛ) находится на уровне не ниже 2. В то же время у всех обанкротившихся предприятий КТЛ был зафиксирован на уровне не выше 1,1. Используя эти данные и модель равномерного распределения вероятностей, оцените вероятности утраты платежеспособности для предприятия с КТЛ на уровне 1,5.

Решение.

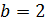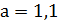Принимаем и , тогда вероятность банкротства составит:

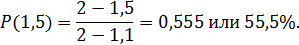
Пример 2.15.

Фирма собирается купить партию товара, цена которого обычно не выходит за пределы 250-500 у.е. Найти вероятность того, фирме удастся закупить товар по цене не дороже 350 у.е., т.к. на более дорогую покупку у фирмы средств нет.

Решение.

Вероятность покупки по цене дороже 350 у.е. равна:

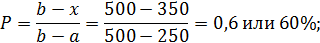
а вероятность покупки по цене не дороже 350 у.е.:

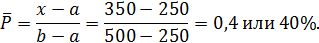
Пример 2.16.

На основании следующей группировки предприятий определите границы зоны неопределенности и с помощью модели равномерного распределения оцените вероятность неплатежеспособности предприятия с уровнем коэффициента текущей ликвидности (КТЛ) 1,5. Исходные данные о численности предприятий по отдельным группам представлены в таблице.

Величина КТЛ	2,1	2,0	1,9	1,8	1,7	1,6	1,5	1,4	1,3	1,2	1,1
Предприятия с устойчивой платежеспособностью								-
Предприятия, утратившие платежеспособность

Решение.

По данным таблицы Тогда для предприятия с значением вероятность неплатежеспособности: