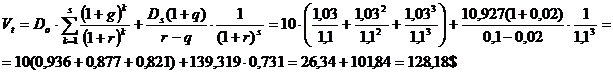Модели оценки обыкновенных акций
Наиболее распространенным методом оценки акций является метод, основанный на оценке их будущих поступлений, т.е. на применении формулы  . В зависимости от предполагаемой динамики дивидендов конкретное представление этой формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:
. В зависимости от предполагаемой динамики дивидендов конкретное представление этой формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:
• дивиденды не меняются;
• дивиденды возрастают с постоянным темпом прироста;
• дивиденды возрастают с изменяющимся темпом прироста.
Вариант с неизменными дивидендами аналогичен ситуации с привилегированными акциями, т.е. применяется формула 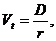 где D – размер дивиденда, r – требуемая норма прибыли. Если выплачиваются одинаковые дивиденды в течение всего времени, темп прироста дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.
где D – размер дивиденда, r – требуемая норма прибыли. Если выплачиваются одинаковые дивиденды в течение всего времени, темп прироста дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.
Пример.Компания гарантирует выплату дивидендов в размере 6 тыс. руб. на акцию в конце каждого года в течение неопределенно долгого времени. Имеет ли смысл покупать акции этой компании по цене 35 тыс. руб., если можно поместить деньги на депозит под 15% годовых?
Решение: 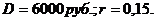
Из формулы 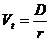 следует, что истинная стоимость акции составляет
следует, что истинная стоимость акции составляет 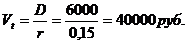 , следовательно, целесообразно приобрести акции по предлагаемой цене 35 тыс. руб.
, следовательно, целесообразно приобрести акции по предлагаемой цене 35 тыс. руб.
Вариант с постоянными темпами роста дивидендов. В этом случае предполагается, что выплачиваемые дивиденды растут от периода к периоду в одной пропорции. Соответствующая модель называется моделью постоянного роста.
Пусть базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна 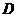 . Ожидается, что дивиденды будут ежегодно увеличиваться с темпом прироста
. Ожидается, что дивиденды будут ежегодно увеличиваться с темпом прироста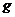 . Тогда по окончании первого года периода прогнозирования будет выплачен дивиденд в размере
. Тогда по окончании первого года периода прогнозирования будет выплачен дивиденд в размере 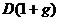 , по окончании второго года -
, по окончании второго года - 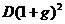 , по окончании k-го года – в размере
, по окончании k-го года – в размере 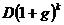 и т.д. Тогда формула
и т.д. Тогда формула  примет вид:
примет вид:
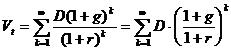
Последнее выражение представляет собой геометрическую прогрессию с первым членом 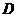 и знаменателем
и знаменателем 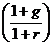 . Как известно, при
. Как известно, при 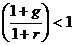 , т. е. при
, т. е. при 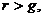 ее сумма может быть найдена по формуле:
ее сумма может быть найдена по формуле: 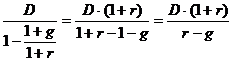 .
.
Следовательно, 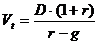 .
.
Данная формула называется моделью Гордона и имеет смысл при 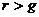 . Очевидно, что числитель формулы этой представляет собой первый ожидаемый дивиденд фазы постоянно роста.
. Очевидно, что числитель формулы этой представляет собой первый ожидаемый дивиденд фазы постоянно роста.
Пример.Компания за прошедший год выплатила 2,7 тыс. руб. на акцию. Согласно прогнозам дивиденды по акциям этой компании будут расти на 4% ежегодно в течение неопределенно долгого времени. Сделать вывод о целесообразности покупки акций компании по цене 20 тыс. руб., если можно поместить деньги на депозит под 14% годовых.
Решение: 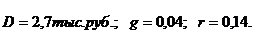 ,
,
Определим теоретическую стоимость акции:
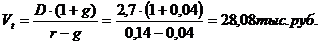
Так как стоимость акции с позиции инвестора превышает ее цену 20 тыс. руб., то имеет смысл приобрести акцию.
Вариант с изменяющимися темпами прироста дивидендов. При оценке акций, дивиденды которых возрастают с изменяющимся темпом прироста, используется модель переменного роста.
а) Предположим, что инвестор прогнозирует, что с высокой вероятностью наступит такой период S, после которого дивиденды будут расти с постоянным темпом 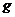 . До наступления S-го периода инвестор прогнозирует величину дивидендов по годам в размере:
. До наступления S-го периода инвестор прогнозирует величину дивидендов по годам в размере: 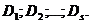
В этом случае теоретическая стоимость акции определяется по формуле:
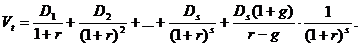
Пример.В течение последующих четырех лет компания планирует выплачивать дивиденды соответственно по 1,2; 1,8; 2; 2,4 долл. на акцию. Ожидается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом 5% в год. Рассчитайте теоретическую стоимость акции, если рыночная норма прибыли составляет 14%.
Решение: 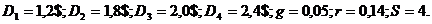
Теоретическая стоимость акции:
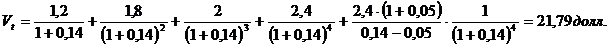
Таким образом, в условиях эффективного рынка акции данной компании на момент оценки должны продаваться по цене, примерно равной 21,79 долл.
б) Согласно формуле Гордона текущая цена обыкновенной акции очень чувствительна к параметру 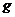 : даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста. Так, если выделить два подынтервала с темпами прироста
: даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста. Так, если выделить два подынтервала с темпами прироста 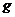 и
и 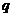 соответственно, то формула
соответственно, то формула 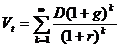 принимает вид:
принимает вид:
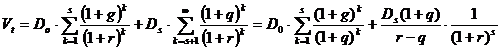
где 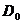 — дивиденд, выплаченный в базисный момент времени;
— дивиденд, выплаченный в базисный момент времени;
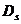 — прогноз дивиденда в
— прогноз дивиденда в 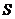 -м периоде
-м периоде
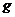 — прогноз темпа прироста дивиденда в первые
— прогноз темпа прироста дивиденда в первые 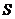 периодов;
периодов;
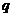 — прогноз темпа прироста дивидендов в последующиепериоды.
— прогноз темпа прироста дивидендов в последующиепериоды.
Пример.За прошедший год компания выплатила в качестве дивидендов по 10$ на акцию. Ожидается, что в течение следующих трех лет дивиденд будет расти на 3% в год, затем темп прироста снизится до 2% в год на весь оставшийся период. Определить теоретическую стоимость акции, если рыночная норма прибыли составляет 10%.
Решение: D0 =10$; g = 0,03; q =0,02; S = 3.