Определение внутренней нормы доходности инвестиций
Внутренняя норма доходности IRR (international rate of return) - показатель, широко используемый при оценке эффективности инвестиционных проектов.
Реализация любого инвестиционного проекта требует привлечения финансовых ресурсов, за которые необходимо платить. Так за заемные средства платят проценты, за привлеченный акционерный капитал -дивиденды и т.д.
Показатель, характеризующий относительный уровень этих расходов, является ценой за использованный (авансируемый) капитал. При финансировании проекта из различных источников этот показатель определяется по формуле средней арифметической взвешенной.
Чтобы обеспечить доход от инвестированных средств или, по крайней мере, их окупаемость, необходимо добиться такого положения, когда чистая текущая стоимость будет больше нуля или равна нулю.
Для этого необходимо подобрать такую процентную ставку дисконтирования членов потока платежей, которая обеспечит получение неотрицательного чистого приведенного дохода (NPV 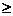 0).
0).
Такая ставка должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке с учетом фактора риска.
Поэтому под внутренней нормой доходности понимают ставку дисконтирования, использование которой обеспечивает равенство текущей стоимости денежных оттоков и текущей стоимости ожидаемых денежных притоков, т.е. при начислении на сумму инвестиций процентов по ставке, равной внутренней норме доходности, обеспечивается получение распределенного по времени дохода.
Показатель внутренней нормы доходности – IRR характеризует максимально допустимый относительный уровень расходов, которые могут быть произведены при реализации данного проекта.
Например, если для реализации проекта получена банковская ссуда, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным.
Таким образом, смысл этого показателя заключается в том, что инвестор должен сравнить полученное значение IRR с ценой привлеченных финансовых ресурсов (cost of capital - CC).
Если IRR>СС, то проект следует принять;
IRR<СС – проект следует отвергнуть;
IRR=СС – проект ни прибыльный, ни убыточный.
Практическое применение данного метода сводится к последовательной итерации, с помощью которой находится дисконтирующий множитель, обеспечивающий равенство NPV=0.
При этом алгоритм решения следующий.
Ориентируясь на существующие в момент анализа процентные ставки на ссудный капитал, выбирают два значения коэффициента дисконтирования 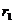 <
< 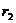 таким образом, чтобы в интервале [
таким образом, чтобы в интервале [ 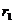 ,
, 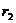 ] функция
] функция 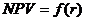 меняла свое значение с «+» на «− » или наоборот. Затем используют формулу:
меняла свое значение с «+» на «− » или наоборот. Затем используют формулу:
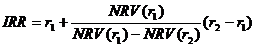 ,
,
где 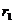 - значение процентной ставки в дисконтном множителе, при котором
- значение процентной ставки в дисконтном множителе, при котором 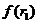 >0
>0 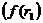 <0);
<0);
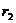 - значение процентной ставки в дисконтном множителе, при котором
- значение процентной ставки в дисконтном множителе, при котором 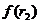 <0
<0 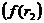 >0).
>0).
Точность вычислений обратно пропорциональна длине интервала [ 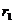 ,
, 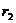 ]. Наиболее точный результат достигается в случае, когда длина интервала минимальна, т.е. когда
]. Наиболее точный результат достигается в случае, когда длина интервала минимальна, т.е. когда 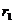 и
и 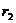 - ближайшие друг к другу значения коэффициента дисконтирования, в случае изменения знака NPV с «+» на «-» удовлетворяющие условиям:
- ближайшие друг к другу значения коэффициента дисконтирования, в случае изменения знака NPV с «+» на «-» удовлетворяющие условиям:
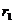 - значение коэффициента дисконтирования, минимизирующее положительное значение NPV,т.е.
- значение коэффициента дисконтирования, минимизирующее положительное значение NPV,т.е. 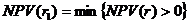 ;
;
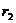 - значение коэффициента дисконтирования, максимизирующие отрицательное значение показателя NPV, т.е.
- значение коэффициента дисконтирования, максимизирующие отрицательное значение показателя NPV, т.е. 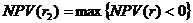 в случае изменения знака NPV с «+» на «-»).
в случае изменения знака NPV с «+» на «-»).
Подобным же образом описывается ситуация для случая когда функция меняет знак с «−» на «+».
Пример. Определить значение внутренней нормы доходности IRR для проекта, рассчитанного на 3 года, требующего инвестиции в размере 20 млн. руб. и имеющего предполагаемые денежные поступления в размере 6 млн. руб.(первый-год), 8 млн.руб. (второй год) и 14 млн.руб. (третий год).
Решение:
Возьмем два произвольных значения процентной ставки для коэффициента дисконтирования 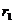 =15% и
=15% и 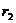 =20%.
=20%.
Соответствующие расчеты сведем в таблицу:
| Год | Денежный поток | Расчет I | Расчет II | ||
Дисконтный множитель для 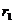 =15% =15% | 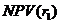 | Дисконтный множитель для 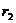 =20% =20% | 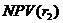 | ||
| 0-й | −20,0 | 1,0 | −20,0 | 1,0 | −20,0 |
| 1-й | 6,0 | 0,8696 | 5,2176 | 0,8333 | 4,9998 |
| 2-й | 8,0 | 0,7561 | 6,0488 | 0,6944 | 5,5552 |
| 3-й | 14,0 | 0,6575 | 9,2050 | 0,5787 | 8,1018 |
| Σ | +0,4714 | −1,3432 |
Для расчета IRR применим формулу:
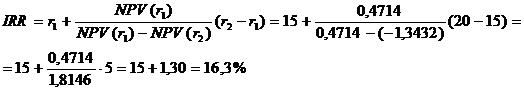
Уточним величину ставки. Для этого примем значения процентных ставок, равными 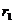 =16% и
=16% и 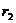 =17% , т.к. 16,3
=17% , т.к. 16,3 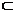 (16, 17).
(16, 17).
Произведем новый расчет.
| Год | Денежный поток | Расчет I | Расчет II | ||
Дисконтный множитель для 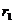 =16% =16% | 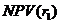 | Дисконтный множитель для 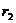 =17% =17% | 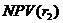 | ||
| 0-й | −20,0 | 1,0 | −20,0 | 1,0 | −20,0 |
| 1-й | 6,0 | 0,8662 | 5,1972 | 0,8547 | 5,1282 |
| 2-й | 8,0 | 0,7432 | 5,9200 | 0,7305 | 5,8440 |
| 3-й | 14,0 | 0,6407 | 8,9698 | 0,6244 | 8,7416 |
| Σ | +0,0870 | −0,2862 |
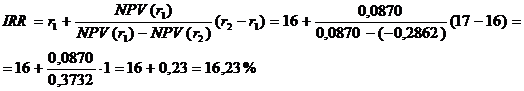
Таким образом, IRR=16,23 является верхним пределом процентной ставки, по которой фирма может окупить кредит для финансирования инвестиционного проекта. Для получения прибыли фирма должна брать кредит по ставке менее 16,23%.
