Начисление процентов в условиях инфляции и налогообложения.

В рассмотренных выше методах определения наращенной суммы не учитывались такие моменты, как налоги и инфляция. Затронем эту проблему.

Следствием инфляции является падение покупательной способности денег, которое за период n характеризуется индексом J_c. Индекс покупательной способности равен обратной величине индекса цен J_p, т.е.

J_c=1/J_p.

Индекс цен J_p показывает, во сколько раз выросли цены за указанный промежуток времени. Указанные индексы должны относиться к одинаковым интервалам времени.

Наращение по простым процентам.Если наращенная за n лет сумма денег составляет S, а индекс цен равен J_p, то реально наращенная сумма денег, с учетом их покупательной способности, равна

C = S / J_p.

Нетрудно связать индекс цен и темп инфляции. Под темпом инфляции h понимается относительный прирост цен за период, обычно он измеряется в процентах и определяется как

h =100(J_p–1).

В свою очередь

J_p =(1+h/100).

Инфляция является цепным процессом. Следовательно, индекс цен за несколько периодов равен произведению цепных индексов цен:

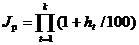, (3.1)

где h_t – темп инфляции в периоде t. В частности, при неизменном темпе прироста цен h за один период (например, h – ожидаемый (или прогнозируемый) темп инфляции) за n периодов получим

J_p =(1+h/100)ⁿ. (3.2)

Пример 27. Постоянный темп инфляции на уровне 2% в месяц приводит к росту цен за год в размере

J_p = (1+h/100)ⁿ =1,02¹²=1,268.

Таким образом, действительный годовой темп инфляции равен 26,8%.

Пусть приросты цен по месяцам составили: 1,5; 1,2 и 0,5%. Индекс цен за 3 месяца равен J_p =1,015·1,012·1,005=1,0323. Темп инфляции за 3 месяца – 3,23%.

Если наращение производится по простой ставке i в течение n лет, то реальное наращение при темпе инфляции h составит

C = S / J_p= .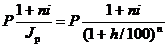

Как видно из формулы, увеличение наращенной суммы с учетом ее инфляционного обесценения имеет место только тогда, когда 1+ni>J_p. Процентная ставка, которая при начислении простых процентов компенсирует инфляцию, равна

i = (J_p–1)/n.

Один из способов компенсации обесценения денег заключается в увеличении ставки процентов на величину так называемой инфляционной премии. Скорректированная таким образом ставка называется брутто-ставкой. Брутто-ставка r находится из равенства скорректированного на инфляцию множителя наращения по брутто-ставке множителю наращения по реальной ставке процента:

,

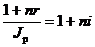откуда

.

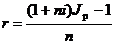Пример 28. На сумму 1500 ден. ед. в течение трех месяцев начисляются простые проценты по ставке 28% годовых. Ежемесячная инфляция характеризуется темпами 2,5; 2,0; 1,8%. Найти наращенную сумму с учетом обесценивания.

Решение. Наращенная сумма равна 15·(1+0,25·0,28)=1605 ден. ед.

Индекс цен J_p= 1,025·1,02·1,018=1,06432.

Наращенная сумма с учетом обесценивания составит:

1605/1,06432=1507,85 ден. ед.

Пример 29. Вы разместили средства в виде полугодового депозита под ставку 40% годовых. Но темп инфляции составил 35% годовых. Какова реальная ставка процентов?

Решение. r =0,4; h =40%; n =½.

Индекс цен J_p за полгода равен J_p =(1+h/100)ⁿ = 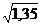=1,161895.

i =((1+nr)/ J_p–1)/n=((1+0,2)/1,161895–1)·2=0,06559, т.е. 6,559%.

Наращение по сложным процентам. Наращенная по сложным процентам сумма к концу срока ссуды с учетом падения покупательной способности денег составит

C = S / J_p= ,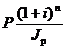

где индекс цен J_p определяется выражением (3.1) или (3.2) в зависимости от непостоянства или постоянства темпа инфляции.

В этом случае падение покупательской способности денег компенсируется при ставке i=h, обеспечивающей равенство C=P. Только в ситуации, когда h/100<i, происходит реальное накопление.

Применяются два способа компенсации потерь от снижения покупательной способности денег при начислении сложных процентов.

1) Корректировка ставки процентов, по которой производится наращение, т.е. на величину инфляционной премии. Ставка процентов, увеличенная на величину инфляционной премии, называется брутто-ставкой (r). Считая, что годовой темп инфляции равен h (выражен в виде десятичной дроби), можем написать равенство соответствующих множителей наращения

,

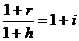где i – реальная ставка. Отсюда

r = i+h+ih,

т.е. инфляционная премия равна h+ih.

2) Индексация первоначальной суммы P. В этом случае сумма P корректируется согласно движению заранее оговоренного индекса. Тогда

S = P J_p (1+i)ⁿ. (3.3)

Нетрудно заметить, что в обоих случаях в итоге приходим к формуле наращения (3.3), в которой в правой части первые два сомножителя отражают индексацию первоначальной суммы, а последние два – корректировку ставки процента.

Пример 30. Предполагаемый темп инфляции 12% в год. Какую ставку сложных процентов нужно проставить в контракте, если желательна реальная доходность 8%? Чему равна инфляционная премия?

Решение. r = i+h+ih =0,08+0,12+0,08·0,12=0,2096, т.е. примерно 21%.

Инфляционная премия равна 21%–8%=13%.

Измерение реальной ставки процента.На практике приходится решать и обратную задачу – находить реальную ставку процента в условиях инфляции. Из тех же соотношений между множителями наращения нетрудно вывести формулы, определяющие реальную ставку i по заданной брутто-ставке r.

При начислении простых процентов годовая реальная ставка процентов равна

.

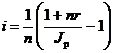При начислении сложных процентов реальная ставка процентов определятся следующим выражением

.

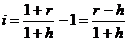Учет налогов.В ряде стран проценты, получаемые кредитором или вкладчиком, облагаются налогом. Это, конечно, уменьшает величину реально получаемой наращенной суммы. Расчет этой суммы можно представить следующим образом.

Обозначим наращенную сумму до уплаты налогов, как и раньше, через S, а после уплаты – через C. Пусть ставка налогов равна g.

Тогда, при начислении простых процентов, получаем, что сумма налога равна Ig = (S – P)g, а наращенная сумма после уплаты налогов

C = S – (S – P)g = S (1– g)+ Pg = P (1+n ((1– g) i).

Это выражение означает, что при начислении простых процентов учет налога сводится к соответствующему сокращению процентной ставки: для получения реального наращения следует вместо ставки i применять ставку (1– g) i.

При начислении налога на сложные проценты, применяемые обычно в средне- и долгосрочных операциях, возможны два варианта расчета: определение налога за весь срок сразу, и расчет процентов за каждый год в отдельности. Первый вариант удобен, когда налоговая ставка в пределах облагаемого налогом периода остается неизменной. Второй оказывается единственно возможным, когда налоговая ставка их года в год меняется.

В первом варианте расчета сумма налога за весь срок равна

(S – P)g= P ((1+i)ⁿ –1)g,

а наращенная сумма после выплаты налога

C = S – (S – P)g = S (1– g)+ Pg = P ((1– g)(1+i)ⁿ +g).

Во втором варианте сумма налога рассчитывается за каждый истекший год. Поскольку речь идет о сложных процентах, ясно, что сумма процентов будет из года в год возрастать, соответственно будет меняться и сумма налога.

Обозначим сумму налога за год t через G_t. Ее можно найти с помощью следующего рекуррентного выражения

G_t = I_t g= (S_t –S_t–1)g =P((1+i)^t–(1+i)^{t –1})g.

Если налоговая ставка постоянна, то сумма налогов за весь срок, рассчитанная первым способом, равна сумме налогов, рассчитанных за соответствующие годы вторым способом.

Ломбардный кредит

Ломбардный кредит означает, что заемщик должен обеспечить получаемый кредит ценными бумагами или материальными ценностями. При этом в мировой практике принято, что сумма ломбардного кредита не должна составлять более 75-80% номинальной стоимости залога. Если кредит обеспечен ценными бумагами, его сумма рассчитывается, исходя из 75-80% текущей курсовой стоимости данных ценных бумаг.

Обычно ломбардный кредит выдается на трехмесячный срок. При этом возможны различные варианты выплаты долга: заемщик может весь долг погасить вовремя; может продлить срок погашения на следующие три месяца; может выплатить вовремя лишь часть долга, а оставшуюся часть погашать в следующем периоде. При расчетах проценты выплачиваются вперед, учитывается точное количество дней в месяце при временной базе – 360 дней (схема 365/360). Если заемщик не погасит кредит вовремя, он, как правило, должен рассчитаться с кредитором по увеличенной (штрафной) процентной ставке в течение всего времени просрочки платежа.

Приведем некоторые примеры расчета.

Пример 31. Клиент обратился в банк 16 марта для получения ломбардного кредита и предоставил в залог 150 ед. ценных бумаг. Величина займа рассчитывается, исходя из 80% их курсовой стоимости. Процентная ставка составляет 9%, а затраты банка по обслуживанию долга – 200 ден. ед. На какой кредит может рассчитывать клиент банка, если курс его ценных бумаг на день обращения составил 300 ден. ед.?

Решение. Расчет производится 16.03.

Общая стоимость ценных бумаг – 150 ед.·300 ден.ед.= 45000ден.ед.

Величина займа – 80% от 45000, т.е. 0,8·45000=36000 ден.ед.

Проценты с 16.03. по 16.06.: I=P(t/K)i=36000·(92/360)·0,09=828 ден. ед. (t =(31–16)+30+31+16=92). С учетом затрат банка на руки клиент получит 36000–828–200 =34972 ден. ед. А 16.06. должен будет вернуть 36000 ден. ед.

Пример 32. Предположим, что в примере 32 заемщик выплатил 16.06 только часть долга – 6000 ден. ед., и продлил погашение кредита еще на три месяца. Необходимо определить, каков остаток долга и проценты за него, сколько всего заплатит должник кредитору.

Решение. Расчет производится 16.06.

Долг на 16.06 составляет 36000 ден. ед. Выплата – 6000 ден. ед. Остаток долга составит 36000-3000=30000 ден. ед.

Должник выплачивает: проценты с 16.06 по 16.09 (92 дня/9%)

I=30000·(92/360)·0.09=690 ден. ед. Итого: 6000+690=6690 ден. ед.

4. Контрольная работа
(для студентов ОЗО)

Пусть N1, N2 –– две последние цифры номера студенческого билета (или номера зачетной книжки). Например, для №9742743 N1 = 4, N2 = 3.

ØЗадача 1. За какое время капитал величиной 60000+4000·(N1+1) руб., вложенный с (N2+10)–го мая под 9% годовых (k, 365), увеличится на такую же величину, как и капитал 200000 руб., вложенный с (N2+2)–го мая по (N1+1)–го августа под (N1+7)% годовых (схема 365/360)?

ØЗадача 2. Долговое обязательство выписано на сумму 5000+20·(N1+ +N2) руб. с уплатой через (200+N1·10+N2) дней, предусматривая, что стоимость кредита составляет 20% этой суммы. Чему равна доходность кредитора, измеряемая простой ставкой наращения i и учетной ставкой d?

ØЗадача 3. В договоре зафиксирована переменная ставка сложных процентов, определяемая как 15% годовых плюс маржа: 8% в первый год, 5% – во второй год, 4% – в третий и четвертый годы. Определить величину коэффициента наращения за 4 года при полугодовом начислении процентов и наращенную величину капитала, если первоначальный капитал составил 5000 рублей.

ØЗадача 4. Для погашения долга величиной 1000·(N1+4)+10·(N2 +3) руб. со сроком погашения 25.06 заемщик выписал своему кредитору векселя: один – на сумму 300·(N1+1) руб. со сроком погашения 27.08, второй – на сумму 200·N1 руб. со сроком погашения 10.09 и третий вексель со сроком погашения 15.12. Найти, какова номинальная величина этого векселя при учетной ставке 8% годовых.

ØЗадача 5. Найти ежемесячную уравнивающую (эффективную) процентную ставку для полугодовой процентной ставки (N1+2)%.

ØЗадача 6. Оценить, сколько будет стоить в конце февраля следующий поток платежей пренумерандо: с января по апрель – по 1500·(N1+2) руб., затем с мая по декабрь – по 1000·(N2+2) руб. при полугодовой процентной ставке 10%.

ØЗадача 7. Составить амортизационный план возврата (равными долями в конце месяца) кредита размером 1000·(N1+4)+10·(N2+3) руб., выданного сроком на 6 месяцев под (N1+10)% годовых.

ØЗадача 8. Платежное обязательство уплатить через 100 дней 4000 руб. с процентами, начисляемыми по ставке простых процентов p=15% годовых (временная база – 365 дней), было учтено за 40 дней до срока погашения по учетной ставке d=20% годовых (временная база – 360 дней). Требуется определить сумму, получаемую при учете.

Библиографический список.

1. Башарин Г.П. Начала финансовой математики. М.: ИНФРА-М, 1997.

2. Ковалев В.В., Финансовыйанализ. М.: Финансы и статистика, 1997. Гл. 4.

3. Кочович Е. Финансовая математика. Теория и практика финансово-банковских расчетов. Пер. с сербского. М.: Финансы и статистика, 1994.

4. Кутуков В.Б. Основы финансовой и страховой математики. М.: ДЕЛО, 1998.

5. Четыркин Е.М. Финансовая математика. М.: ДЕЛО, 2001.