По выполнению практических и лабораторных работ
МЕТОДЫ ОПТИМИЗАЦИИ
Учебное пособие
По выполнению практических и лабораторных работ
Часть I
вЕЛИКИЙ НОВГОРОД
ББК Печатается по решению
РИС НовГУ
Рецензент
кандидат технических наук, доцент В.В. Сокол
МЕТОДЫ ОПТИМИЗАЦИИ. Учебное пособие по выполнению практических и лабораторных работ. Часть 1. / Сост.: А.С. Орлов, В.А. Орлов; Нов ГУ им. Ярослава Мудрого. – Великий Новгород, 2006.
Учебное пособие, состоящее из трех частей, подготовлено с целью оказания практической помощи в повышении уровня знаний по дисциплине «МЕТОДЫ ОПТИМИЗАЦИИ».
В первой части рассматриваются модели линейного программирования и алгоритмы их реализации с помощью MS EXCEL. Содержится поэтапная характеристика решения типовых задач, варианты заданий для самостоятельного решения, включая дополнительные повышенной сложности и список рекомендуемой литературы.
Учебное пособие предназначено для студентов экономических специальностей.
ÓНовгородский государственный
университет, 2006
Ó А.С. Орлов, В.А. Орлов
составление 2006
Содержание
Стр.
Введение……………………………………………………………………….3
- ЛАБОРАТОРНАЯ РАБОТА №1.РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL…………………………6
1.2.Варианты заданий к лабораторной работе для самостоятельного выполнения
- ЛАБОРАТОРНАЯ РАБОТА №2. ПРЕОДОЛЕНИЕ НЕСОВМЕСТНОСТИ ОГРАНИЧЕНИЙ………………………………………………………………
- ЛАБОРАТОРНАЯ РАБОТА №3. ПАРАМЕТРИЧЕСКИЙ АНАЛИЗ……..
Список литературы………………………………………………………….23
Введение
Линейное программирование (ЛП) послужило основой для разработки многих других математических методов исследования операций, например целочисленного, стохастического и нелинейного программирования. Важно и то, что после четырех десятилетий глубоких разработок, практической реализации и критического анализа результатов применение методов линейное программирование привело к значительным успехам в решении широкого круга задач, относящихся к таким сферам, как промышленное производство, военное дело, сельское хозяйство, экономические исследования, транспорт, здравоохранение и даже психология и социальные науки.
В данной лабораторной работе рассмотрены компьютерные методы ЛП. Процесс оптимизации с помощью MS Excel позволяет проиллюстрировать приемы анализа моделей на чувствительность. В заключительной части дается экономическая интерпретация линейной оптимизационной модели.
В этой работе рассматривается построение математической модели и решение оптимизационной задачи ЛП. При изучении материала обратите особое внимание па допущения, сделанные при построении модели, и те последствия, которые они могут вызвать при реализации полученного решения. Рассматривая конкретный пример, попытайтесь сделать обобщающие выводы о применимости использованных процедур в других ситуациях.
ЛАБОРАТОРНАЯ РАБОТА №1
РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL
1 Цель лабораторной работы
Научиться составлять математическую модель и находить оптимальное решение.
2 Задание (пример) к лабораторной работе
Решить задачу распределения ресурсов. Определить, в каком количестве надо выпускать продукцию каждого типа, чтобы получить максимальную прибыль. Для этого необходимо выполнить следующее:
1. Создать форму для ввода условий задачи.
2. Ввести исходные данные в виде таблицы.
3. Ввести в отдельные ячейки таблицы зависимости из математической модели.
4. Найти оптимальное решение с помощью команды Поиск решения/меню Сервис.
5. Получить оптимальное решение задачи распределения ресурсов, вывести на экран три типа отчетов: по результатам, по устойчивости, по пределам и тщательно проанализировать их.
6. Привести свои выводы и предложения по поводу получившихся результатов оптимизации данной задачи.
Исходные данные
Выпускается продукция четырех типов: продукт 1, продукт 2, продукт 3, продукт 4.
· Для выпуска требуется 3 вида ресурсов: труд, сырье, финансы.
Известно:
· Нормы расхода (количество ресурса каждого вида), необходимые для выпуска единицы продукции данного типа.
· Сколько ресурса имеется в наличии.
· Прибыль, получаемая от реализации единицы каждого типа продукции.
Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы.
Оформим данные в виде таблицы 1:
Таблица 1 - Таблица представления результатов
| Ресурс | Продукт 1 | Продукт 2 | Продукт 3 | Продукт 4 | Знак | Наличие |
| Прибыль | мах | |||||
| Трудовые | <= | |||||
| Сырьевые | <= | |||||
| Финансовые | <= |
Рисунок 1 – Компьютерный эквивалент задачи
2 Введите исходные данные в форму.
3 Далее введите зависимости для целевой функции и левой части ограничений:
- Курсор ставим в клетку F6, выбираем команду Мастер функций на панели инструментов и щелкаем левой кнопкой мыши. На экране появляется диалоговое окно Мастер функций шаг 1 из 2. Устанавливаем курсор в окно Категория на категорию Математические функции, щелкаем левой кнопкой мыши и выбираем курсором в окне Функции Суммпроизв. Щелкаем на кнопку мыши.
Нажимаем на команду Далее. Открывается диалоговое окно Мастер функций, где в строке массив 1 вводим диапазон ячеек B$3:E$3. Следует заметить, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.
В массив 2 ввести B6:E6. Затем щелкаем на кнопку ОК.
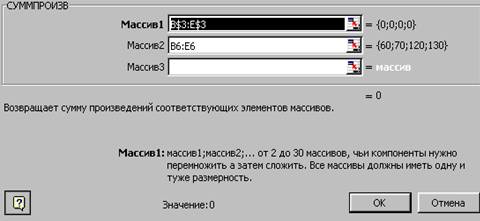 |
Рисунок 2 – Функция MS Excel СУММПРОИЗВ
Устанавливаем курсор в клетку F6 и копируем эту формулу в диапазон F9:F11.
На этом ввод данных закончен.Он оформляется в виде (3):
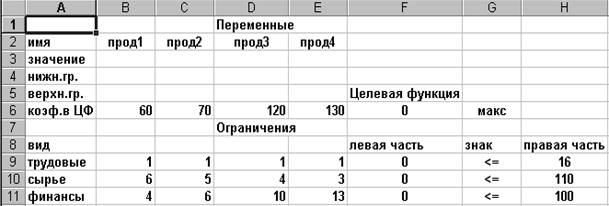 |
Рисунок 3 – Итоговая таблица ввода исходных данных
4 Организация поиска решений.
В меню Сервис выбираем команду Поиск решения. Следующие действия производятся в диалоговом окне.
Уставить целевую ячейку (щелкнуть мышкой в F6)
В этом же диалоговом окне указываем, какое значение должна принимать целевая функция (максимальное или минимальное).
Вводим адреса искомых переменных, для этого ставим курсор в поле Изменяя ячейки и вводим адреса: B3:E3.
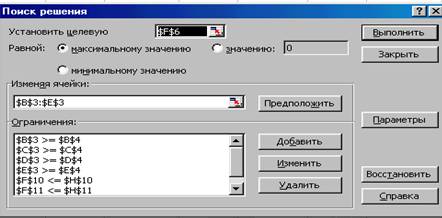 |
Далее нажмите кнопку Добавить.
Рисунок 4 – Окно ПОИСК РЕШЕНИЯ
На экране появится диалоговое окно Добавление ограничения.
 |
Рисунок 5 – Окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ
Вводим граничные условия на переменные.
В окне Ссылка на ячейку ввести B3. Курсор устанавливаем на стрелку и щелкаем на левую кнопку мыши. Устанавливаем курсор на знак >= и щелкаем на левую кнопку мыши. Переводим курсор в правое окно и вводим там B4. Щелкаем мышкой на команду Добавить. На экране опять появится диалоговое окно Добавление ограничения. Аналогично вводим граничные условия для остальных переменных.
$B$3>=$B$4
$C$3>=$C$4
$D$3>=$D$4
$E$3>=$E$4
Аналогично вводим и другие ограничения:
F9<=H9, F10<=H10, F11<=H11.
После ввода последнего ограничения вместо Добавить ввести Ок. На экране появится диалоговое окно Поиск решения с введенными условиями.
Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью команд Изменить…, Удалить.
На этом ввод условий задачи заканчивается. На очереди следующий шаг – решение задачи.
Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения.
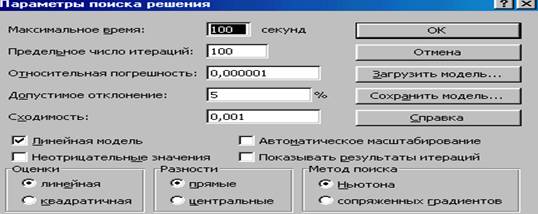 |
Выбираем опцию Параметры… На экране появляется диалоговое окно Параметры поиска решения.
Рисунок 6 – Окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ
-- С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. С наиболее важными командами, применимыми при решении конкретных задач, мы будем знакомиться по мере необходимости. Вместе с тем, команды, используемые по умолчанию, подходят для решения большей части практических задач.
-- Устанавливаем флажок Линейная модель, что обеспечивает применение симпликс – метода.
-- Ок.
-- На экране появляется уже знакомое диалоговое окно Поиск решения.
-- Выполнить.
На экране: диалоговое окно Результаты поиска решения. Решение найдено и результат оптимального решения задачи приведены в таблице.
 |
Рисунок 7 – Окно РЕЗУЛЬТАТЫ ПОИСКА РЕШЕНИЯ
На экране появляется оптимальное решение. Оно представлено в виде таблицы 2:
Таблица 2 - Оптимальное решение задачи линейного программирования
| Переменные | |||||||
| имя | прод1 | прод2 | прод3 | прод4 | |||
| значение | |||||||
| нижн.гр. | |||||||
| верхн.гр. | Прибыль | направление | |||||
| прибыль | макс | ||||||
| Ограничения | |||||||
| вид | левая часть | знак | правая часть | ||||
| трудовые | <= | ||||||
| сырье | <= | ||||||
| финансы | <= |
Результаты моделирования
. Вызовем на экран диалоговое окно Результат поиска решения (т. е. произведите операцию поиска решения заново).
Щелкнем на тип отчета : Результаты/ОК. Внизу экрана появится надпись Отчет по результатам, щелкните по ней мышкой. Аналогично получим отчет по устойчивости. Эти отчеты представлены в таблицах 3 и 4.
Таблица 3 - Отчет по результатам
| Microsoft Excel 8.0e Отчет по результатам | ||||||
| Рабочий лист: [лабораторная работа №5.xls]Лист1 | ||||||
| Отчет создан: 20.09.02 12:23:13 | ||||||
| Целевая ячейка (Максимум) | ||||||
| Ячейка | Имя | Исходно | Результат | |||
| $F$6 | Прибыль | |||||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходно | Результат | |||
| $B$3 | продукция1 | |||||
| $C$3 | продукция2 | |||||
| $D$3 | продукция3 | |||||
| $E$3 | продукция4 | |||||
| Ограничения | ||||||
| Ячейка | Имя | Значение | формула | Статус | Разница | |
| $F$9 | трудовые ресурсы | $F$9<=$H$9 | связанное | |||
| $F$10 | сырьевые ресурсы | $F$10<=$H$10 | не связан. | |||
| $F$11 | финансовые ресурсы | $F$11<=$H$11 | связанное | |||
| $B$3 | продукция1 | $B$3>=$B$4 | не связан. | |||
| $C$3 | продукция2 | $C$3>=$C$4 | связанное | |||
| $D$3 | продукция3 | $D$3>=$D$4 | не связан. | |||
| $E$3 | продукция4 | $E$3>=$E$4 | связанное |
Таблица 4 - Отчет по устойчивости
| Microsoft Excel 8.0e Отчет по устойчивости | |||||||
| Рабочий лист: [лабораторная работа №5.xls]Лист1 | |||||||
| Отчет создан: 20.09.02 12:24:00 | |||||||
| Изменяемые ячейки | |||||||
| Результ. | Нормир. | Целевой | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | стоимость | Коэффициент | Увеличение | Уменьшение | |
| $B$3 | продукция1 | ||||||
| $C$3 | продукция2 | -10 | 1E+30 | ||||
| $D$3 | продукция3 | ||||||
| $E$3 | продукция4 | -20 | 1E+30 | ||||
| Ограничения | |||||||
| Результ. | Теневая | Ограничение | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | Цена | Правая часть | Увеличение | Уменьшение | |
| $F$9 | трудовые ресурсы | ||||||
| $F$10 | сырьевые ресурсы | 1E+30 | |||||
| $F$11 | финансовые ресурсы |
Структура отчетов
1.Отчет по результатам состоит из трех таблиц:
--- Таблица 1 приводит сведения о целевой функции.
--- Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи.
--- Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
2. Отчет по устойчивости состоит из двух таблиц:
--- В первой таблице приводятся следующие значения для переменных:
· Результат решения задачи;
· Нормируемая стоимость, т. е. дополнительные двойственные переменные, которые показывают, на сколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;
· Коэффициенты целевой функции;
· Придельные значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.
--- В таблице 2 приводятся аналогичные значения для ограничений:
· Величина использованных ресурсов;
· Теневая цена, т. е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
· Значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Для нелинейных моделей отчет по устойчивости содержит данные для градиентов и множителей Лагранжа (нормируемая стоимость и теневые цены) или, как еще они называются в американской литературе, объективно - обусловленные оценки (двойственные оценки).
3. Отчет по пределам показывает, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения:
· Приводятся значения, полученные для продукции 1,2,3 и 4 видов в оптимальном решении;
· Приводятся нижние пределы изменения значений этих продукций.
Анализ полученных отчетов
Таким образом, для получения максимального дохода (прибыли) в данной модели следует производить 10 единиц продукции 1 вида и 6 единиц продукции 3 вида. Прибыль при этом составит 1320 $. Любое другое сочетание производимой продукции приведет к снижению прибыли.
В данной модели трудовые и финансовые ресурсы использованы полностью. Их недоиспользование приведет к снижению прибыли в расчете на единицу трудовых ресурсов на 20 $, на 1 $ финансовых ресурсов прибыли снизится на 10 $ (теневая цена из отчета устойчивости).
Показатель нормируемая стоимость из отчета по устойчивости показывает, что включение в производство продукции второго и четвертого видов нецелесообразно, экономически невыгодно предприятию, т. к. производство продукции в объеме одна единица приведет к снижению прибыли на 10 и 20 $ соответственно (нормируемая стоимость для этих видов продукции отрицательна). Нулевые двойственные оценки (нулевая нормируемая стоимость) переменных показывают, что производство продукции 1 и 3 вида экономически выгодно. Степень выгодности производства продукции 2 и 4 видов в данном случае выражается количественно.
Так как трудовые и финансовые ресурсы использованы полностью, то ограничения являются жесткими (связанными). Их смягчение привело бы к увеличению прибыли. В данном случае – это привлечение трудовых и финансовых ресурсов (это привлечение будет эффективным, пока сырьевые ресурсы не будут исчерпаны).
В столбце целевой результат указаны значения целевой функции при выпуске данного типа продукции на нижнем приделе. Так, при значении 720 видно, что F=60*0+70*0+120×6+130*0=720.
Выводы и предложения
В оптимальном решении мы получили, что производство продукции 2 и 4 видов экономически невыгодно. С одной стороны, при этом мы будем получать максимально возможную прибыль, но с другой - сокращается ассортимент продукции, то есть продукция предприятия не будет полностью удовлетворять потребностям потребителей. Спрос на продукцию упадет, следовательно, упадет и прибыль предприятия. Для повышения ассортимента продукции (для включения в производство 2 и 4 видов продукции) необходимо:
· по возможности привлечь дополнительные трудовые и финансовые ресурсы;
· повысить цены на 2 и 4 виды продукции;
· повысить их качество;
· снизить затраты на их производство;
· повысить производительность труда при производстве 2 и 4 видов продукции.
Ввод в производство 2 и 4 видов продукции позволит увеличить прибыль предприятия, но для ее выпуска необходимо привлечь дополнительные инвестиции и принять на работу дополнительный рабочий персонал. То есть, если есть возможность привлечь дополнительные трудовые и финансовые ресурсы, то нужно расширять производство и увеличивать ассортимент выпускаемой продукции.
4 Варианты заданий к лабораторной работе для самостоятельного выполнения
Условие задачи в общем виде:
Фирма пpоизводит два вида пpодукции - А и В. Объем сбыта пpодукции вида А составляет не менее 20% общего объема pеализации пpодукции обоих видов. Для изготовления пpодукции А и В используется одно и то же сыpье, суточный запас котоpого огpаничен величиной b2кг. При этом продукции В нужно получить не менее b1 единиц. Расход сыpья на единицу пpодукции А составляет а3 кг., а на единицу пpодукции В -- а4кг. Фирма имеет финансовые ресурсы в размере b3 тыс. руб и трудовые b4чел.-дней. Расход денежных средств на ед. продукции составляет а5 и а6 руб., соответственно, и требуются трудовые ресурсы в количестве 1 чел.- дня на производство каждой единицы продукта. Цены пpодукции А и В pавны а1и а2 руб., соответстввенно. Опpеделите оптимальное pаспpеделение сыpья, денежных средств и трудовых ресурсов для изготовления пpодукции А и В.
Пусть х1 и х2 - объем производства (ед.) продукции А и В соответственно. Требуется рассчитать такие значения х1 и х2, чтобы общая прибыль от производства была максимальной.
Указание. Составить соответствующую задачу математического программироваия и решить ее графически, симплекс - методом и с помощью функции ПОИСК РЕШЕНИЯ MS EXCEL.
Задачу решить при следующих значениях констант aj и bi в соответствии с номером варианта, указанного преподавателем:
| Номер | Варианта| a1¦ a2 ¦ a3 ¦ a4 ¦ a5 ¦a6 ¦ b1 ¦ b2 ¦ b3 ¦ b4 |
¦ 0 ¦ 5 ¦ 7 ¦ 0.06 ¦ 0.05 ¦ 0.1 ¦ 0.3 ¦ 100¦ 170 ¦ 630 ¦ 160
¦ 1 ¦ 4 ¦ 6 ¦ 0.05 ¦ 0.06 ¦ 0.4 ¦ 0.2 ¦ 1000¦ 300 ¦ 300 ¦ 170
¦ 2 ¦ 4 ¦ 5 ¦ 0.07 ¦ 0.04 ¦ 0.1 ¦ 0.03¦ 500¦ 220 ¦ 900 ¦ 200
¦ 3 ¦ 3 ¦ 6 ¦ 0.06 ¦ 0.03 ¦ 0.3 ¦ 0.04¦ 1000¦ 120 ¦ 600 ¦ 210
¦ 4 ¦ 4 ¦ 5 ¦ 0.06 ¦ 0.04 ¦ 0.6 ¦ 0.2 ¦ 750¦ 240 ¦ 800 ¦ 250
¦ 5 ¦ 6 ¦ 4 ¦ 0.05 ¦ 0.03 ¦ 0.2 ¦ 0.2 ¦ 250¦ 150 ¦ 600 ¦ 180
¦ 6 ¦ 3 ¦ 4 ¦ 0.04 ¦ 0.05 ¦ 0.1 ¦ 0.4 ¦ 1000¦ 180 ¦ 890 ¦ 1350
¦ 7 ¦ 6 ¦ 4 ¦ 0.05 ¦ 0.05 ¦ 0.4 ¦ 0.2 ¦ 1000¦ 150 ¦ 800 ¦ 1850
¦ 8 ¦ 5 ¦ 3 ¦ 0.07 ¦ 0.03 ¦ 0.2 ¦ 0.2 ¦ 1500¦ 180 ¦ 800 ¦ 3000
¦ 9 ¦ 3 ¦ 5 ¦ 0.04 ¦ 0.04 ¦ 0.1 ¦ 0.3 ¦ 1000¦ 200 ¦ 600 ¦ 2500
¦ 10 ¦ 4 ¦ 5 ¦ 0.05 ¦ 0.05 ¦ 0.2 ¦ 0.4 ¦ 1100¦ 150 ¦ 700 ¦ 1200
¦ 11 ¦ 8 ¦ 4 ¦ 0.03 ¦ 0.07 ¦ 0.4 ¦ 0.5 ¦ 1000¦ 120 ¦ 550 ¦ 1600
¦ 12 ¦ 5 ¦ 6 ¦ 0.06 ¦ 0.05 ¦ 0.1 ¦ 0.3 ¦ 1000¦ 180 ¦ 800 ¦ 900
¦ 13 ¦ 4 ¦ 7 ¦ 0.07 ¦ 0.06 ¦ 0.4 ¦ 0.3 ¦ 1000¦ 310 ¦ 630 ¦ 1000
¦ 14 ¦ 4 ¦ 6 ¦ 0.06 ¦ 0.04 ¦ 0.2 ¦ 0.2 ¦ 1150¦ 295 ¦ 600 ¦ 1000
¦ 15 ¦ 3 ¦ 5 ¦ 0.07 ¦ 0.03 ¦ 0.3 ¦ 0.3 ¦ 850¦ 126 ¦ 850 ¦ 1000
¦ 16 ¦ 5 ¦ 4 ¦ 0.04 ¦ 0.04 ¦ 0.1 ¦ 0.4 ¦ 1000¦ 240 ¦ 650 ¦ 1200
¦ 17 ¦ 4 ¦ 5 ¦ 0.05 ¦ 0.03 ¦ 0.1 ¦ 0.2 ¦ 850¦ 150 ¦ 750 ¦ 900
¦ 18 ¦ 3 ¦ 4 ¦ 0.06 ¦ 0.05 ¦ 0.4 ¦ 0.2 ¦ 919¦ 180 ¦ 700 ¦ 1500
¦ 19 ¦ 6 ¦ 4 ¦ 0.07 ¦ 0.05 ¦ 0.3 ¦ 0.4 ¦ 925¦ 170 ¦ 730 ¦ 2000
¦ 20 ¦ 6 ¦ 5 ¦ 0.04 ¦ 0.03 ¦ 0.2 ¦ 0.2 ¦ 988¦ 150 ¦ 600 ¦ 1500
¦ 21 ¦ 3 ¦ 3 ¦ 0.05 ¦ 0.04 ¦ 0.2 ¦ 0.2 ¦ 994¦ 200 ¦ 800 ¦ 1700
¦ 22 ¦ 5 ¦ 7 ¦ 0.06 ¦ 0.05 ¦ 0.1 ¦ 0.3 ¦ 500¦ 190 ¦ 500 ¦ 1900
¦ 23 ¦ 6 ¦ 6 ¦ 0.07 ¦ 0.06 ¦ 0.2 ¦ 0.4 ¦ 1000¦ 205 ¦ 550 ¦ 3300
¦ 24 ¦ 7 ¦ 7 ¦ 0.07 ¦ 0.06 ¦ 0.4 ¦ 0.4 ¦ 1000¦ 210 ¦ 850 ¦ 2300
¦ 25 ¦ 3 ¦ 6 ¦ 0.06 ¦ 0.05 ¦ 0.3 ¦ 0.3 ¦ 500¦ 170 ¦ 650 ¦ 1930
-------------------------------------------------------------------------
МЕТОДЫ ОПТИМИЗАЦИИ
Учебное пособие
по выполнению практических и лабораторных работ
Часть I
вЕЛИКИЙ НОВГОРОД
ББК Печатается по решению
РИС НовГУ
Рецензент
кандидат технических наук, доцент В.В. Сокол
МЕТОДЫ ОПТИМИЗАЦИИ. Учебное пособие по выполнению практических и лабораторных работ. Часть 1. / Сост.: А.С. Орлов, В.А. Орлов; Нов ГУ им. Ярослава Мудрого. – Великий Новгород, 2006.
Учебное пособие, состоящее из трех частей, подготовлено с целью оказания практической помощи в повышении уровня знаний по дисциплине «МЕТОДЫ ОПТИМИЗАЦИИ».
В первой части рассматриваются модели линейного программирования и алгоритмы их реализации с помощью MS EXCEL. Содержится поэтапная характеристика решения типовых задач, варианты заданий для самостоятельного решения, включая дополнительные повышенной сложности и список рекомендуемой литературы.
Учебное пособие предназначено для студентов экономических специальностей.
ÓНовгородский государственный
университет, 2006
Ó А.С. Орлов, В.А. Орлов
составление 2006
Содержание
Стр.
Введение……………………………………………………………………….3
- ЛАБОРАТОРНАЯ РАБОТА №1.РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL…………………………6
1.2.Варианты заданий к лабораторной работе для самостоятельного выполнения
- ЛАБОРАТОРНАЯ РАБОТА №2. ПРЕОДОЛЕНИЕ НЕСОВМЕСТНОСТИ ОГРАНИЧЕНИЙ………………………………………………………………
- ЛАБОРАТОРНАЯ РАБОТА №3. ПАРАМЕТРИЧЕСКИЙ АНАЛИЗ……..
Список литературы………………………………………………………….23
Введение
Линейное программирование (ЛП) послужило основой для разработки многих других математических методов исследования операций, например целочисленного, стохастического и нелинейного программирования. Важно и то, что после четырех десятилетий глубоких разработок, практической реализации и критического анализа результатов применение методов линейное программирование привело к значительным успехам в решении широкого круга задач, относящихся к таким сферам, как промышленное производство, военное дело, сельское хозяйство, экономические исследования, транспорт, здравоохранение и даже психология и социальные науки.
В данной лабораторной работе рассмотрены компьютерные методы ЛП. Процесс оптимизации с помощью MS Excel позволяет проиллюстрировать приемы анализа моделей на чувствительность. В заключительной части дается экономическая интерпретация линейной оптимизационной модели.
В этой работе рассматривается построение математической модели и решение оптимизационной задачи ЛП. При изучении материала обратите особое внимание па допущения, сделанные при построении модели, и те последствия, которые они могут вызвать при реализации полученного решения. Рассматривая конкретный пример, попытайтесь сделать обобщающие выводы о применимости использованных процедур в других ситуациях.
ЛАБОРАТОРНАЯ РАБОТА №1
