Основные правила ввода данных в ячейку таблицы
Данные вводятся на рабочий лист электронной таблицы порциями, обычно последовательно вводят информацию в несколько соседних ячеек, поочередно заполняя каждую из них. При нажатии пользователем алфавитно-цифровой клавиши текущая клетка таблицы автоматически переходит в режим ввода, готовясь принять данные, распознать их тип, хранить полученное значение и выводить его в заданном формате.
Для ввода данных необходимо:
сделатьзаполняемуюклетку текущей (перевести туда рамку указателя);
набратьпоследовательность символов на клавиатуре, при этом вводимая строка в Excel отображается и в заполняемой клетке, и над полем таблицы в строке формул;
закончить ввод нажатием клавиши ввода Enter (¿), либо щелчком мыши по заменяющей ее экранной кнопке с изображением зеленой галочки (символ a ), расположенной в режиме ввода над полем рабочего листа в левой части строки ввода.
FДля исправления допущенных при наборе опечаток после выхода из режима ввода можно
повторить ввод данных в ту же клетку;
отредактировать содержимое ячейки в строке формул
отредактировать содержимое текущей клетки, дважды щелкнув по ней мышью, или нажав клавишуF2.
FОтменить незаконченный ввод можно клавишейEsc, или экранной кнопкой с красным крестиком (символr ) в строке ввода (строке формул).
FЕсли данные набраны правильно, но введены ошибочно не в ту клетку, их можно перенести:
методом перетаскивания: подведя снизу указатель мыши к рамке выделенной ячейки с данными (он должен принять форму толстой белой стрелки), нажать левую кнопку и, удерживая ее, перемещать манипулятор, ориентируясь на пунктирную рамку положения клетки, принимающей перенос.
Выполнив команды ВЫРЕЗАТЬ и ВСТАВИТЬ
FДля полной очистки текущей клетки от ранее введенной информации нажимайте клавишу Delete.
В зависимости от состава вводимой информации, и особенно от её первого символа (префикса) данных электронные таблицы автоматически относят их после ввода к одному из двух типов: константа или формула. Табличные формулы начинаютсяс префикса и могут состоять из:
числовых констант,
знаков действий и скобок,
адресов и/или имен табличных диапазонов и отдельных клеток,
имен встроенных функций.
Префиксомформулы,с которого х обязательно начинается ее ввод служит символ «=»
При вводе последовательности символов, не начинающейся с префикса формулы, данные интерпретируется программой как константа – число, дата или текст.
Числовое выражение может состоять только из цифр, знаков "плюс", "минус"круглых и фигурных скобоки некоторых других знаков, предусмотренных дробным, процентным, экспоненциальным, денежным и финансовым форматами.
Даты хранятся как целые числа, хотя формат их записи больше похож на текст.
Текстом являются любые данные, которые программе не удается распознать как число или формулу, в том числе и данные, подразумеваемые как числа и формулы, при вводе которых были допущены ошибки.
Текст при вводе выравнивается по левому краю ячейки, а даты, числа и формулы - по правому. Если формат вывода значения числового выражения (константы или результата формулы) не помещается на экране в ширину клетки, то вместо него для привлечения внимания пользователя выводится "заборчик" знаков нумерации «########». Если же в ширину столбца не укладывается текст, а ячейка справа по строке уже занята, то окончание длинного текста усекается.
Подбор параметра
Зачастую Вы знаете тот результат, который нужно получить с помощью вычисления по формуле , однако, входное значение , необходимое для получения этого результата , Вам не известно. Перебор возможных значений этого параметра (подгонка результата) достаточно утомительное и трудоемкое занятие.
Чтобы решить эту задачу, целесообразно воспользоваться заложенным в Excel средством подбора параметра. Excelварьирует значение в заданной ячейке до тех пор, пока вычисление по формуле, зависящей от этой ячейки, не даст желаемый результат.
FКогда следует применять подбор параметра
Для того, чтобы найти определенное значение для какой – либо ячейки путем подбора значения другой отдельной ячейки необходимо воспользоваться командой СЕРВИСÞПОДБОР ПАРАМЕТРА
FКак применять команду ПОДБОР ПАРАМЕТРА
Для того чтобы найти определенное значение, удовлетворяющее формуле:
Выделите ячейку, которая содержит эту формулу
Выполните команду СЕРВИСÞПОДБОР ПАРАМЕРА
Рассмотрим работу этой команды на примере.
Пример 6‑1
В таблице приведена калькуляция, в которой отражены расходы и доходы от реализации некоторой продукции.
Зададимся целью получить прибыль 50 млн. рублей.
Каким образом это можно сделать?
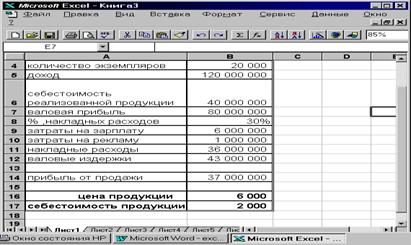
Рис. 6‑2 Рабочий лист Excel с исходными данными примера
Очевидно, можно попытаться увеличить количество реализованной продукции, снизить уровень накладных расходов, величину валовых издержек и др.
Проще всего - поднять цену на единицу продукции (чаще всего незадачливые предприниматели именно так и поступают).
Выполним команду СЕРВИСЮПОДБОР ПАРАМЕТРА...
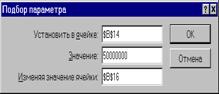
Рис. 6‑3. Диалоговое окно «Подбор параметра...»
В открывшемся диалоговом окне «Подбор параметра»
в качестве целевой ячейки укажем адрес ячейки, содержащей значение прибыли от продажи,
в поле «Значение» - укажем желаемую сумму прибыли,
в поле «Изменяя значение ячейки» - укажем адрес ячейки, содержащей цену изделия.
Щелкнем на кнопке «ОК», начав тем самым процесс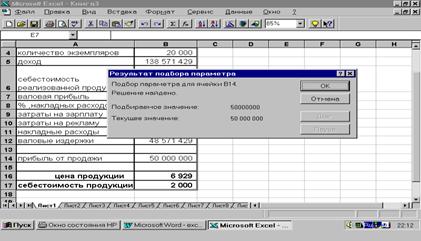 
подбора параметра
Рис. 6‑4. Результат выполнения подбора параметра
Если же Ваши конкуренты выпустили подобную продукцию по более низкой цене, то, очевидно, придется менять тактику и снижать, например, себестоимость и повторять процедуру подбора параметра, для определения величины необходимого снижения себестоимости.
Правила подбора параметра
В окна «Установить в ячейке» и «Изменяя ячейку» можно вводить как ссылки на ячейки, так и их имена
Изменяемая ячейка должна содержать значение, от которого прямо или косвенно зависит формула, указанная в окне «Установить в ячейке»
Изменяемая ячейка не должна содержать формулу
Когда подбор параметра завершен, Excel выводит результаты на рабочий лист и в окно «Состояние параметра».
39. Для сохранения полученных результатов нажмите кнопку «ОК»
40. Для восстановления исходных значений нажмите кнопку «Отмена»
41. Если Вы решили сохранить найденное решение на рабочем листе, а затем передумали, выберите в меню ПРАВКА команду ОТМЕНИТЬ ПОДБОР ПАРАМЕТРА сразу же после завершения операции подбора параметра
Диспетчер сценариев
Очень часто оказывается интересным сохранить различные варианты решения задачи с тем, чтобы потом выбрать наиболее приемлемый вариант. Либо представить их в виде структурной или сводной таблицы для последующего анализа.
MS Excelпозволяет создавать и сохранять в виде сценариев наборы входных значений, приводящих к различным результатам .
Сценарий– это множество входных значений,называемых изменяемыми ячейками, которое сохраняется под указанным Вами именем. Каждому набору изменяемых ячеек соответствует набор предположений «Что –если…[47]», который Вы применяете к модели рабочего листа, чтобы проследить, как значения изменяемых ячеек влияют на другие значения модели.
FДля каждого сценария может быть задано до 32 изменяемых ячеек.
Диспетчер сценариев позволяет выполнять следующее:
Создавать составные сценарии с множеством наборов изменяемых ячеек.
Просматривать результаты примения каждого сценария на рабочем листе
Создавать итоговый отчет по всем входным значениям и результатам.
Объединять сценарии из одной руппы в единую модель сценариев
Защищать сценарии от их изменения и скрывать их
Ослеживать модификации с помощью автоматического ведения истории сценария.
Сценарии удобно применять в тех случаях, когда необходимо исследовать модель «Что-если…» с неопределенными переменными.
Предположим, Вы намерены составить бюджет на следующий год, не имея точной информации о размере годового дохода. С помощью диспетчера сценариев Вы сформируете разные сценарии, выполните для них анализ «Что-если…» и сохраните эти сценарии вместе с моделью..
Рассмотрим построение сценариев на примере.
Пример 6‑2
В таблице приведены данные о деятельности предприятия
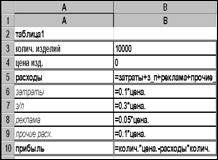
Рис. 6‑5 Таблица расчета прибыли предприятия (учтены только переменные издержки) в зависимости от цены на изделие и количества выпускаемых изделий.
Используя данные таблицы и команду СЕРВИСÞСЦЕНАРИИ, проанализируем, как повлияет изменение стоимости единицы изделия на величину прибыли и величину расходов на изготовление изделия. Расчеты произведем для стоимостей изделия 5, 7.5,10, 12.5и15 рублей.
Решение
Выполните команду СЕРВИСÞСЦЕНАРИИ
В открывшемся диалоговом окне щелкните на кнопке «Добавить»
Во вновь открывшемся диалоговом окне «Добавление сценария»введите:
в окно "Название сценария" введите его название, например «Вариант 1»
в окно «Изменяемые ячейки» введите адрес ячейки, значение которой Вы будете изменять при работе по сценарию (в нашем случае это адрес ячейки, содержащей цену изделия)
в окно «Примечание» введите поясняющий текст, например «Влияние цены на прибыль и расходы на изготовление изделия»
Щелкните на кнопке ОК
В открывшемся окне «Значение ячеек сценария» введите значение изменяемой ячейки (5)
Щелкните на кнопке «Добавить»
Во вновь открывшемся диалоговом окне «Добавление сценария» повторите вышеописанные действия, последовательно вводя в окно новые значения изменяемой ячейки.
После ввода последнего значения изменяемой ячейки, щелкните на кнопке ОК
В открывшемся окне «Диспетчер сценариев» щелкните на кнопке «Отчет» ( при необходимости изменения расчетов по какому-либо сценарию, выделите его и щелкните на кнопке «Изменить»)
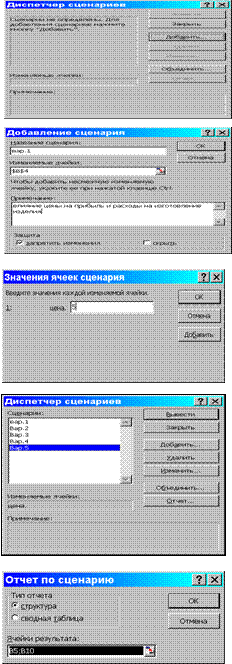
Рис. 6‑6. Диалоговые окна диспетчера сценариев
В открывшемся окне «Отчет по сценарию»выберите:
Тип отчета (например, структура)
В окне «Ячейки результата» введите адреса ячеек, результаты расчетов которых будут включены в отчет (например, В5 (Расходы)и В10 (прибыль))
Щелкните на кнопке ОК
Отредактируйте отчет:
Удалите столбец D
Измените ширину столбцов
Постройте на отдельном листе диаграмму (график) иллюстрирующую зависимость величины прибыли и расходов от цены изделия
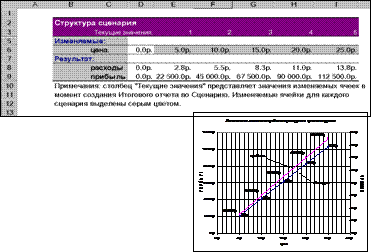Отредактируйте построенную диаграмму таким образом, чтобы она имела вид подобный, показанному на рисунке
Рис. 6‑7 Отчет и диаграмма, построенные по сценариям
Таблица подстановки
Для введенных на рабочий лист формул можно выполнить анализ «Что – если», позволяющий проследить, как изменение определенных значений в формулах влияет на результаты вычислений по этим формулам.
Анализ «Что – если» выполняется при помощи таблицы данных – интервала ячеек ,в котором выводятся результаты подстановки различных значений в одну или несколько формул.
Таблица данных позволяет:
Быстро вычислить несколько итераций для одной операции
Просмотреть и сравнить на рабочем листе результаты всех возможных подстановок.
Существует два типа таблиц подстановки:
Таблица подстановки с одним входом. Вы вводите разные значения для одной переменной и наблюдаете их влияние на результат вычисления одной или нескольких формул
Таблица подстановки с двумя входами. Вы вводите разные значения для двух переменных и наблюдаете их влияние на результат вычисления одной формулы.
Наиболее часто в практике финансового анализа используется табица подстановок с одним входом.
Как использовать таблицу данных с одним входом
С помощью таблицы данных с одним входом Вы проследите, как изменения одной переменной влияют на одну или несколько формул.
Пример 6‑3
Рассмотрим использование таблицы данных с одним входом на примере расчета ежемесячных выплат, необходимых для погашения ссуды в размере 200тыс. руб. взятой на 3 года в при различных процентных ставках.
Для расчета используется функции ППЛАТ[48]из категории функции “Финасовые”
Синтаксис функции: ППЛАТ (норма, кпер,нз,бс,тип)
где
норма- годовая процентная ставка (норма дисконтирования0
кпер –общее число периодов выплат
нз –начальная величина займа (или вклада)
бс, тип - не обязательные параметры
Решение
На листе Excel постройте таблицу, подобную показанной на рисунке.
ячейках А2:В4 разместите условия задачи
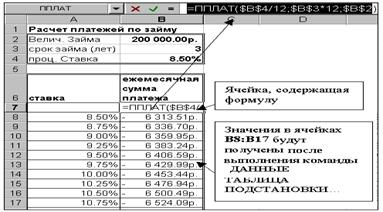
В ячейке В7 разместите формулу: «=ППЛАТ($B$4/12;$B$3*12;$B$2)»
Рис. 6‑8 Фрагмент таблицы Excel для расчета платежей по займу
Обратите внимание на аргументы функции
$B$4/12 –величина месячной процентной ставки (норма)
$B$3*12 –количество периодов выплат для погашения ссуды(кпер)
$B$2- величина займа (нз)
Выделите диапазон ячеек, содержащий исходные значения процентных ставок и формулу для расчета – А7:В17
Выполните команду ДАННЫЕÞТАБЛИЦА ПОДСТАНОВОК…На экране появится диалоговое окно «Таблица подстановок»
 |
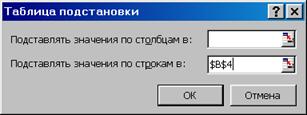Рис. 6‑9. Диалоговое окно «Таблица подстановок»
Открывшееся диалоговое окно используется для задания рабочей ячейки на которую ссылается формула расчета. В нашем примере, это ячейка В4,которую и необходимо указать в поле «Подставлять значения по строкам в:»диалогового окна в абсолютных координатах (абсолютная ссылка).
Если исходные данные расположены в строке, то ссылку на рабочую ячейку необходимо ввести в поле «Подставлять значения по столбцам в»
При нажатии на кнопку «ОК» Excel заполнит столбец, как показано на рисунке.
Если в таблицу необходимо включить большее количество формул, использующих исходные значения (в нашем примере «Процентные ставки»), то дополнительные формулы вставляются справа от существующей в той же строке. Затем необходимо вновь выделить всю таблицу, включая полученные ранее значения, и заполнить диалоговое окно команды ДАННЫЕÞТАБЛИЦА ПОДСТАНОВОК.
Приложение 2. Порядковые номера дней в не високосном году
| День | Месяц | |||||||||||
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь | |
| 1 | ||||||||||||
| 2 | ||||||||||||
| 3 | ||||||||||||
| 4 | ||||||||||||
| 5 | ||||||||||||
| 6 | ||||||||||||
| 7 | ||||||||||||
| 8 | ||||||||||||
| 9 | ||||||||||||
| 10 | ||||||||||||
| 11 | ||||||||||||
| 12 | ||||||||||||
| 13 | ||||||||||||
| 14 | ||||||||||||
| 15 | ||||||||||||
| 16 | ||||||||||||
| 17 | ||||||||||||
| 18 | ||||||||||||
| 19 | ||||||||||||
| 20 | ||||||||||||
| 21 | ||||||||||||
| 22 | ||||||||||||
| 23 | ||||||||||||
| 24 | ||||||||||||
| 25 | ||||||||||||
| 26 | ||||||||||||
| 27 | ||||||||||||
| 28 | ||||||||||||
| 29 | ||||||||||||
| 30 | ||||||||||||
| 31 |
Приложение 3. Множители наращения по сложным процентам
| Число периодов | Ставка процентов за период | ||||||
| 5,00% | 10,00% | 15,00% | 20,00% | 25,00% | 30,00% | 40,00% | |
| 1,05 | 1,1 | 1,15 | 1,2 | 1,25 | 1,3 | 1,4 | |
| 1,1025 | 1,21 | 1,3225 | 1,44 | 1,5625 | 1,69 | 1,96 | |
| 1,157625 | 1,331 | 1,520875 | 1,728 | 1,953125 | 2,197 | 2,744 | |
| 1,215506 | 1,4641 | 1,749006 | 2,0736 | 2,441406 | 2,8561 | 3,8416 | |
| 1,276282 | 1,61051 | 2,011357 | 2,48832 | 3,051758 | 3,71293 | 5,37824 | |
| 1,340096 | 1,771561 | 2,313061 | 2,985984 | 3,814697 | 4,826809 | 7,529536 | |
| 1,4071 | 1,948717 | 2,66002 | 3,583181 | 4,768372 | 6,274852 | 10,54135 | |
| 1,477455 | 2,143589 | 3,059023 | 4,299817 | 5,960464 | 8,157307 | 14,75789 | |
| 1,551328 | 2,357948 | 3,517876 | 5,15978 | 7,450581 | 10,6045 | 20,66105 | |
| 1,628895 | 2,593742 | 4,045558 | 6,191736 | 9,313226 | 13,78585 | 28,92547 | |
| 1,710339 | 2,853117 | 4,652391 | 7,430084 | 11,64153 | 17,9216 | 40,49565 | |
| 1,795856 | 3,138428 | 5,35025 | 8,9161 | 14,55192 | 23,29809 | 56,69391 | |
| 1,885649 | 3,452271 | 6,152788 | 10,69932 | 18,18989 | 30,28751 | 79,37148 | |
| 1,979932 | 3,797498 | 7,075706 | 12,83918 | 22,73737 | 39,37376 | 111,1201 | |
| 2,078928 | 4,177248 | 8,137062 | 15,40702 | 28,42171 | 51,18589 | 155,5681 | |
| 2,182875 | 4,594973 | 9,357621 | 18,48843 | 35,52714 | 66,54166 | 217,7953 | |
| 2,292018 | 5,05447 | 10,76126 | 22,18611 | 44,40892 | 86,50416 | 304,9135 | |
| 2,406619 | 5,559917 | 12,37545 | 26,62333 | 55,51115 | 112,4554 | 426,8789 | |
| 2,52695 | 6,115909 | 14,23177 | 31,948 | 69,38894 | 146,192 | 597,6304 | |
| 2,653298 | 6,7275 | 16,36654 | 38,3376 | 86,73617 | 190,0496 | 836,6826 |
[1] Данное пособие, безусловно, не может полностью охватить предмета «Финансовая математика» и задумано как настольная книга пользователя ПК, помогающая ему, во-первых, самостоятельно изучить основные формулы процентных расчетов и, во-вторых, научиться работать с ними в электронных таблицах.
Принятые в настоящем учебном пособии состав и последовательность рассмотрения учебного материала, позволяют получить целостное представление о финансово-экономических расчетах и о практическом применении этих методов при разработке и реализации финансовых решений.
[2] В дореволюционной литературе очень часто можно встретить слово «Интерес», которое предприниматели использовали для характеристики выгодности какой – либо сделки.
[3] В литературе достаточно часто этот показатель называется коэффициентом или множителем наращения, показывающим во сколько раз наращенная сумма больше первоначальной суммы долга и . по существу может приниматься как базисный темп роста.
[4] Термин дисконтирование в широком смысле означает определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину. Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.
[5] Проценты, начисленные по ставке процентов, называются антисипативными, а по учетной ставке – декурсивными.
[6] Напомним, что «процентные деньги» – это разность между первоначальной денежной суммой (PV) и наращенной денежной сумой (FV) – I =FV – PV.
[7] Этот способ обычно используется в Германии, Дании, Швеции
[8] Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии
[9] Этот способ применяется в Португалии, Англии, США.
[10] Как и в случае простых процентов, множитель наращения показывает будущую стоимость 1 денежной единицы, вложенной на n периодов. Для обозначения этого финансового коэффициента часто используется стандартная аббревиатураFVIF (от англ. Future Value Interest Factor – процентный множитель будущей стоимости). Будущая стоимость определяется умножением размера первоначально инвестированной суммы на этот коэффициент: FV=PV*FVIF(n,r)
r
[11] Напомним, что величина kн=(1 +r)*n –множитель наращения,экономический смысл которого состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке i.
[12] В литературе, посвященной финансовому анализу, такой расчет часто называют приведением стоимостного показателя к заданному моменту времени, а величину PV называют приведенной (современной или текущей) величиной FV
[13] Вексель – обязательство вернуть указанную в векселе сумму (номинал векселя, обозначим его S), в указанный срок. Если держатель векселя (его собственник в данный момент) желает обменять вексель на деньги, он обращается в банк с предложением учесть имеющийся у него вексель, т.е. купить его за сумму Р, меньшую, чем номинал S. Такая сделка называется дисконтированием, а сумма скидки с номинала – дисконтом
[14] Дисконтирование может быть также связано и с проведением кредитной операции при начислении процентов в начале интервала начисления и заемщик получает сумму PV за вычетом процентных денег D из наращиваемой суммы кредита FV, подлежащей к возврату
[15] Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т.е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.
[16] Обратите внимание, что величины n и d могут оказаться такими, что nd > 1и, соответственно, величина PV будет меньше нуля. Это, конечно же, невозможно: никто не согласится отдать вексель, да еще уплатить за это сумму равную FV*(n*d-1).Поэтому дисконтирование применяют так, чтобы было 1 > n*d > 0.
[17] Если финансовая функция вызывается для продолжения ввода другой функции (вложенная функция)
[18] Возможен также вариант непосредственного ввода формулы, содержащей имена и параметры встроенных финансовых функций.
Формула должна начинаться со знака «=». Далее следует имя функции. В круглых скобках указываются ее аргументы, в последовательности соответствующей синтаксису функции. В качестве разделителя аргументов обычно используется точка с запятой. Так например, формула определения будущей стоимости инвестиции при непосредственном ее вводе в ячейку таблицы может иметь вид: БС(ставка;кпер;Плт;ПС;тип) = БС(5%;5;;-10000)
[19] Диалоговое окно «Диспетчер функций» может быть также вызвано командой ВСТАВКАðФУНКЦИЯ…
[20] В некоторых случаях при неполной инсталляции MS Office в этом списке могут содержаться только основные команды. Для того, чтобы в дальнейшем выводился полный список имен функций, выполните команду СЕРВИСðНАДСТРОЙКИ… и в открывшемся окне установите «флажок» «Пакет Анализа»
[21] В младших версиях MS Excel это диалоговое окно может содержать кнопку «Далее», при щелчке на которой вызывается диалоговое окно самой функции.
[22] Microsoft Excel хранит даты как целые числа и может выполнять над ними вычисления. По умолчанию 1 января 1900 года имеет порядковый номер – 1, и, соответственно, 1 сентября 2006г будет иметь порядковый номер – 38961, так как интервал в днях между этими датами равен 38961,
[23] Использование функции «Дата» как вложенной функции будет рассмотрена более подробно в разделе «ДЕНЕЖНЫЕ ПОТОКИ»
[24] В младших версиях MS Excel диалоговое окно функции вызывается двойным щелчком на ячейке, содержащей редактируемую формулу.
[25] Напомним, что в германской практике расчета продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней
[26] Напомним, что в соответствии с французской системой расчета, продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю.
[27] Напомним, что при выпуске ценных бумаг, заключении финансовых контрактов, займов в долговом соглашении обычно указывается годовая номинальная процентная ставкаи период начисления (год, полугодие, квартал и т.д.)
Эффективная процентная ставка – это годовая сложных процентов, обеспечивающая тот же доход, что и m- разовое начисление процентов по ставке r/m.
[28] Заметим, что платежи могут быть неодинаковы не только по знаку и величине самого платежа, но и по времени их поступления.
[29] Заметим, что рассмотренное в предыдущей главе наращение и дисконтирование вложенной суммы может также рассматриваться как денежный поток с однократным поступлением денег и единичным периодом накопления.
[30] Это частный случай потока платежей, все члены которого - положительные величины. Примерами аннуитета могут быть регулярные взносы в пенсионный или другие фонды, выплаты процентов по ценным бумагам, например, по акциям и т.д.
[31] Выплаты по облигациям с фиксированной ставкой купона, банковским кредитам, долгосрочной аренде, страховым полисам, формирование различных фондов – все это далеко неполный перечень финансовых операций, денежные потоки которых, представляют собой обыкновенные аннуитеты.
[32] Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить необходимую наращенную сумму.
[33] Легко видеть, что выражения в квадратных скобках в (4-3) представляет собой множитель, равный современной стоимости аннуитета в 1 денежную единицу. Разделив современную стоимость PVденежного потока любого вида на этот множитель, можно получить величину периодического платежа CFэквивалентного ему аннуитета. Эта математическая зависимость часто используется в финансовом анализе для приведения потоков с неравномерными поступлениями к виду обыкновенного аннуитета
[34] Напомним, что по условиям задачи платежи и начисления процентов производятся в конце года. Таким образом, наращение первой вложенной суммы будет проходить в течение 5-1 =4 лет; наращение второй вложенной суммы – 5-2= 3 года и т.д
[35] Напомним, одновременное нажатие клавиш Ctrl+Shift+Enterпозволяет ввести формулу как формулу для массива данных.
[36] Обратите внимание, что формула заключена в фигурные скобки, что характеризует ее как формулу массива.
[37] Аргумент Нз функции эквивалентен, аргументу Пс, использовавшемуся в других финансовых функциях.
[38] Часть этих функций была нами рассмотрена в главе «ИЗМЕНЕНИЕ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ»
[39] В младших версиях Excel эта функция обозначена как ППЛАТ()
[40] Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия данного проекта.
[41] По сути дела этот показатель определяет срок, в течение которого инвестиции будут "заморожены", так как реальный доход от инвестиционного проекта начнет поступать только по истечении периода окупаемости
[42] Формула реализует условие: если величина накопленного дисконтированного дохода больше нуля, то вычисляется период окупаемости как разность величины накопленного дисконтированного дохода в этот период и разности суммы накопленного дисконтированного дохода в предыдущий период и дисконтированного денежного потока, отнесенной к величине дисконтированного денежного потока.
[43] В том случае, если платежи имеют регулярный характер и даты их поступления не определены, для вычисления величины IRR может быть использована функция ВНДОХ() (либо функция ВСД в версии Excel 2002,2003, XP
[44]В литературе эта величина иногда носит название – средневзвешенная доходность
[45] В том случае, если платежи имеют регулярный характер и даты их поступления не определены, для вычисления величины IRR может быть использована функция ВНДОХ() (либо функция ВСД в версии Excel 2002,2003, XP
[46] В ряде случаев используется альтернативный стиль ссылок на ячейки рабочего листа, когда столбцы также нумеруются, а номер строки указывается в первую очередь, Перейти к альтернативному стилю адресации ячеек можно выполнив команду СЕРВИСð ПАРАМЕТРЫ, выбрав в ее диалоговом окне на вкладке «Общие» в группе«Стиль ссылок» позицию переключателя R1C1. Тогда первая клетка (ячейка) рабочего листа так и будет именоваться R1C1, от английского Row1Column1 (ряд первый, колонка первая).
[47] Ниже будет подробно рассмотрен ситуационный анализ «Что – если…»
[48] Напомним, что, начиная с версии Excel 2000, эта формула обозначена как ПЛТ()