Временная база финансовой операции

В банковской практике разных стран расчетное число дней в году при начислении процентов определяется по-разному: Срок ссуды n может быть как целым, так и дробным положительным числом.

В тех случаях, когда срок ссуды менее года, происходит модификация формулы:

а) если срок ссуды выражен в месяцах(М), то величина n выражается в виде дроби:

n = М / 12, ( 1‑14)

б) если время выражено в днях(t), то величина n выражается в виде дроби:

n = t / T, ( 1‑15)

где t – число дней ссуды, т.е. продолжительность срока, на который выдана ссуда;

T– расчетное число дней в году (временная база).

FВозможны следующие варианты расчета

ðВременную базу ( T ) можно представить по-разному:

условно состоящую из 360 дней. В этом случае речь идет об обыкновенном (ordinary interest), или коммерческом проценте;

взять действительное число дней в году (365 или 366 дней). В этом случае получают точный процент (exact interest).

ðЧисло дней ссуды ( t) также можно по-разному определять:

условно, исходя из того, что продолжительность любого целого месяца составляет 30 дней, а оставшиеся дни от месяца считают точно, – в результате получают так называемое приближенное число дней ссуды;

используя прямой счет или специальные таблицы порядковых номеров дней года, рассчитывают фактическое число дней между датами, – в этом случае получают точное число дней ссуды.

Таким образом, если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех возможных способов:

ðОбыкновенные проценты с приближенным числом дней ссуды, или, как часто называют, "германская практика расчета", когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней[7].

ðОбыкновенные проценты с точным числом дней ссуды, или "французская практика расчета", когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю[8].

ðТочные проценты с точным числом дней ссуды, или "английская практика расчета", когда продолжительность года и продолжительность ссуды берутся точно по календарю[9].

Вполне естественно, что в зависимости от использования конкретной практики начисления простых процентов их сумма будет различаться по абсолютной величине.

Для упрощения процедуры расчета точного числа дней финансовой операции пользуются специальными таблицами порядковых номеров дней года (Приложение 1), в которых все дни в году последовательно пронумерованы. Точное количество дней получается путем вычитания номера первого дня финансовой операции из номера последнего дня финансовой операции.

Переменная ставка

Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях, в силу тех или иных причин, предусматриваются дискретно изменяющиеся во времени процентные ставки. Например, наличие инфляции вынуждает собственника денег периодически варьировать процентной ставкой.

В том случае, если на последовательных интервалах начисления процентов n1, n2, n3,…, n_m устанавливаются разные процентные ставки r₁,r₂, r₃,…, r_m _,то наращенная сумма может быть определена как

FV=PV*(1 +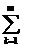n_k*r_k) = PV*k_n ( 1‑16)

где коэффициент наращения (k_n)

k_n =(1 +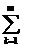n_k*r_k) ( 1‑17)

Пример 1‑3

Сумма в размере 2000 рублей дана в долг на 1 год по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма:

FV=PV(1 +n*r ) = 2000 (1 + 1 * 0.1) = 2200 руб.

или

FV = PV * k_н = 2000 * 1,1 = 2200 руб.

Сумма начисленных процентов:

I = PV * n * r = 2000 * 1 * 0,1 = 200 руб.

или

I = FV - PV = 2200 - 2000 = 200 руб.

Таким образом, через год необходимо вернуть общую сумму в размере 2200 рублей, из которой 2000 рублей составляет долг, а 200 рублей – "цена долга (процентные деньги).

Пример 1‑4

Ссуда выдана под 10% годовых сроком:

а) на 5 месяцев;

б) на 3 месяца.

Определить процентную ставку за срок ссуды.

Решение.

а) n= 5/12 =0.42 r_{5 мес} = 0,1 * 5/12 = 0. 0417;

б) n = 3/12 =0,25; m = 4; r =0,1/4 = 0,025

Пример 1‑5

Ссуда в размере 50000 руб. выдана на полгода по простой ставке 14% годовых. Определить наращенную сумму и сумму начисленных процентов.

Решение

Наращенная сумма

FV=PV(1 +n*r ) =50000*(1+0,5*0,14) = 53500 руб.

Сумма начисленных процентов

I = FV – PV=53500-50000=3500 руб.

Пример 1‑6

Определить сумму вклада, который надо положить в банк сроком на 2 месяца под 10% годовых, чтобы к концу срока получить 110 000 руб.

Решение

FV=110000/(1 + 0,1 * 2/12) = 108196.7 руб.

Пример 1‑7

Клиент внес вклад в банк в сумме 1 тыс. руб. сроком на 1 год. Процентная ставка до середины второго квартала составляла 30 % годовых, далее до конца третьего квартала - 25 %, а с начала четвертого квартала - снова 30%. Какую сумму клиент получил в конце года?

Решение.

Периоды;

ðс начала года до середины второго квартала (n₁) равен 4,5 месяца, или 0,375 года;

ðот середины второго квартала до конца третьего (n₂) равен 4,5 месяца, или 0,375 года;

ðс конца третьего квартала до конца четвертого (n₃) равен 3 месяца, или 0,25 года

Коэффициент наращения:

ðза период до середины второго квартала –

k₁ = 0, 3 * 0, 375 = 0,113,

ðот середины второго квартала до начала четвертого квартала –

k₂ = 0,25*0,375 =0,094.;

ðза четвертый квартал – k₃=0, 3 * 0, 25 = 0,.075

ðза год k год = k₁ + k₂ + k₃ =0,281