Финансовая математика – что это?

Красноярск. 2006.

Министерство науки и образования

Российский государственный социальный университет

Красноярский филиал

Л.А.Левин

Учебно – методичекое пособие

для студентов экономических специальностей

всех форм обучения

Красноярск. 2006.

Левин Л.А. "Финансовая математика в Excel": Учебное - методическое пособие.

Рецензенты:

зав. кафедрой Информатики «Финансы и кредит» КФ РГСУ доцент И.З. Погорелов

декан ФИФТ КГПУ, к.т.н., проф. Е.А Вейсов

Учебное пособие предназначено для освоения дисциплины "Финансовая математика”, а также для тех дисциплин, где изучаются разделы, связанные с вопросами оценки финансовых операций.

Предназначено для студентов экономических специальностей всех форм обучения.

Пособие рассчитано на широкое использование электронной таблицы Excel и содержит основные теоретические положения, финансовой математики, примеры решения задач, вопросы по отдельным разделам. задания для самостоятельного выполнения и библиографию.

Рассмотрено на заседании кафедры

Протокол № ___ “___”_ ______2006__г.

СОДЕРЖАНИЕ

Введение 8

Финансовая математика – что это? 8

Фактор времени в финансово-экономических расчетах 9

MS Excel – основной инстумент для выполнения финансово-экономических расчетов 11

Как работать с учебным пособием? 12

1. Изменение СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ 14

1.1. Основные категории финансово-экономических расчетов 15

1.1.1. Тесты для проверки усвоения пройденного материала 19

1.2. Простые проценты 21

1.2.1. Временная база финансовой операции 23

1.2.2. Переменная ставка 25

1.2.3. Определение срока ссуды и величины процентной ставки 27

1.2.4. Тесты для проверки усвоения пройденного материала 29

1.2.5. Задачи для самостоятельного решения 31

1.3. Сложные проценты 34

1.3.1. Начисление процентов при дробных периодах 38

1.3.2. Эффективная ставка процентов 40

1.3.3. Непрерывное начисление процентов 42

1.3.4. Переменная ставка процентов 44

1.3.5. Определение срока ссуды и величины процентной ставки 45

1.3.6. Тесты для проверки качества усвоения пройденного материала 46

1.3.7. Задачи для самостоятельного решения 48

1.4. Дисконтирование 51

1.4.1. Математическое дисконтирование 52

1.4.2. Банковский учет 54

1.4.3. Тест для проверки качества усвоения пройденного материала 57

1.4.4. Задачи для самостоятельного решения 58

2. Использование встроенных функций MS Excel 61

2.1. Технология работы с финансовыми функциями Excel 61

2.1.1. Операции наращения. Функция БС() 70

Операции дисконтирования 74

Определение срока финансовой операции 75

Определение процентной ставки 76

Расчет эффективной и номинальной ставки процентов 78

Начисление процентов по плавающей ставке 79

3. Потоки платежей и финансовые ренты 81

3.1. Денежные потоки в виде серии равных платежей (аннуитеты) 83

3.2. Классификация финансовых рент 83

3.3. Расчет периодических платежей 86

3.3.1. Определение будущей (наращенной) стоимости потока платежей. Функция БС() 87

3.3.2. Современная (текущая) величина аннуитета. Функция ПС() 89

3.3.3. Нерегулярные потоки платежей, Функция БЗРАСПИС() 92

3.3.4. Определение величины периодического платежа. Функция ПЛТ() 95

3.3.5. Расчет платежей по процентам. Функция ПРПЛТ() 97

3.3.6. Расчет суммы платежей по процентам по займу. Функция ОБЩПЛАТ() 99

3.3.7. Расчет величины основных платежей по займу. Функция ОСПЛТ() 100

3.3.8. Расчет суммы основных платежей по займу. Функция ОБЩДОХОД() 101

3.3.9. Использование операции «Подбор параметра» для определения отдельных параметров аннуитета 102

3.4. Разработка шаблона для анализа аннуитетов 105

3.5. Задания для самостоятельной работы 109

4. Оценка инвестиционных процессов 114

4.1. Чистый приведенный доход 115

4.2. Срок окупаемости 120

4.3. Индекс рентабельности 123

4.3.1. Внутренняя норма доходности. Функция ЧИСТВНДОХ() 125

4.3.2. Модифицированная внутренняя норма доходности. Функция МСВД() 128

4.4. Денежный поток инвестиционного проекта с произвольными периодами поступления платежей 129

4.5. Задачи для самостоятельного решения 132

5. Литература 143

6. Приложения 145

6.1. Приложение 1. Основные технологические приемы работы в MS Excel 145

6.1.1. Перемещение по рабочему листу 146

6.1.2. Основные правила ввода данных в ячейку таблицы 148

6.2. Подбор параметра 150

6.2.1. Правила подбора параметра 152

6.2.2. Диспетчер сценариев 153

6.3. Таблица подстановки 157

6.4. Приложение 2. Порядковые номера дней в не високосном году 160

6.5. Приложение 3. Множители наращения по сложным процентам 162

Введение

В настоящее время трудно переоценить роль специалиста по финансовому анализу деятельности предприятия. Финансы являются “кровью” предприятия. Именно в деньгах оцениваются проданные товары и оказанные клиентам услуги. Именно деньги являются универсальным измерителем необходимых предприятию ресурсов - сырья и материалов, станков, человеческих ресурсов, информации и т.д. Поэтому планирование и прогнозирование, контроль и оптимизация финансовых потоков являются жизненно важными задачами финансовой службы.

Решению этих задач посвящен курс «Финансовая математика».

Простые проценты

Представим себе что кре­дитор и заемщик договариваются о величине кредита PV (первоначальная денежная сумма), размере годовой процентной ставке (r), сроке кредита (T) и длительности периода начисления процентов (n)

Математически такая операция может быть представлена в виде мо­дели простых процентов. По этой модели происходит накопление наращенной суммы FV (общей суммы долга) за счет периодического (например, ежегодного) начисления процентных денег (I)[6]. В соответствии с этим наращенная сумма равна:

к концу первого года –

FV₁ = PV+I

к концу второго года –

FV₂ = PV+2*I

к концу n-го года –

FV_n= PV+n*I

Таким образом, накопление суммы происходит по схеме простых процен­тов и образует возрастающую числовую последовательность:

FV₁, FV₂,…, FV_n,

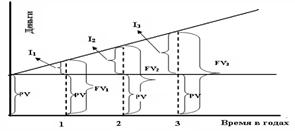которая представляет собой арифметическую прогрессию с первым членом PV и разностью прогрессии I = FV-PV

Рис. 1‑3 Наращивание первоначальной суммы по схеме простых процентов

При использовании простых ставок процентов проценты (процентные деньги) определяются исходя из первоначальной суммы долга. Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов.

Таким образом, размер ожидаемой наращенной суммы долга (дохода) зависит от трех факторов:

величины инвестированной суммы,

уровня процентной ставки,

срока финансовой операции.

В общем случае, модель накопления капитала по схеме простых про­центов принимает вид:

FV = PV + I = PV + n*PV*I = PV*(1 + n*I) ( 1‑12)

Учитывая выражение 3-3 (I = PV*r) модель простых процентов можно записать:

FV = PV + I = PV + r* PV * n = PV* (1 + r *n ) = PV * k_н, (1‑13)

Переменная ставка

Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях, в силу тех или иных причин, предусматриваются дискретно изменяющиеся во времени процентные ставки. Например, наличие инфляции вынуждает собственника денег периодически варьировать процентной ставкой.

В том случае, если на последовательных интервалах начисления процентов n1, n2, n3,…, n_m устанавливаются разные процентные ставки r₁,r₂, r₃,…, r_{m ,} то наращенная сумма может быть определена как

FV=PV*(1 + 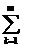n_k*r_k) = PV*k_n ( 1‑16)

где коэффициент наращения (k_n)

k_n =(1 + 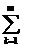n_k*r_k) ( 1‑17)

Пример 1‑3

Сумма в размере 2000 рублей дана в долг на 1 год по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма:

FV=PV(1 +n*r ) = 2000 (1 + 1 * 0.1) = 2200 руб.

или

FV = PV * k_н = 2000 * 1,1 = 2200 руб.

Сумма начисленных процентов:

I = PV * n * r = 2000 * 1 * 0,1 = 200 руб.

или

I = FV - PV = 2200 - 2000 = 200 руб.

Таким образом, через год необходимо вернуть общую сумму в размере 2200 рублей, из которой 2000 рублей составляет долг, а 200 рублей – "цена долга (процентные деньги).

Пример 1‑4

Ссуда выдана под 10% годовых сроком:

а) на 5 месяцев;

б) на 3 месяца.

Определить процентную ставку за срок ссуды.

Решение.

а) n= 5/12 =0.42 r_{5 мес} = 0,1 * 5/12 = 0. 0417;

б) n = 3/12 =0,25; m = 4; r =0,1/4 = 0,025

Пример 1‑5

Ссуда в размере 50000 руб. выдана на полгода по простой ставке 14% годовых. Определить наращенную сумму и сумму начисленных процентов.

Решение

Наращенная сумма

FV=PV(1 +n*r ) =50000*(1+0,5*0,14) = 53500 руб.

Сумма начисленных процентов

I = FV – PV=53500-50000=3500 руб.

Пример 1‑6

Определить сумму вклада, который надо положить в банк сроком на 2 месяца под 10% годовых, чтобы к концу срока получить 110 000 руб.

Решение

FV=110000/(1 + 0,1 * 2/12) = 108196.7 руб.

Пример 1‑7

Клиент внес вклад в банк в сумме 1 тыс. руб. сроком на 1 год. Процентная ставка до середины второго квартала составляла 30 % годовых, далее до конца третьего квартала - 25 %, а с начала четвертого квартала - снова 30%. Какую сумму клиент получил в конце года?

Решение.

Периоды;

ðс начала года до середины второго квартала (n₁) равен 4,5 месяца, или 0,375 года;

ðот середины второго квартала до конца третьего (n₂) равен 4,5 месяца, или 0,375 года;

ðс конца третьего квартала до конца четвертого (n₃) равен 3 месяца, или 0,25 года

Коэффициент наращения:

ðза период до середины второго квартала –

k₁ = 0, 3 * 0, 375 = 0,113,

ðот середины второго квартала до начала четвертого квартала –

k₂ = 0,25*0,375 =0,094.;

ðза четвертый квартал ­– k ₃=0, 3 * 0, 25 = 0,.075

ðза год k год = k₁ + k₂ + k₃ =0,281

В результате в конце года клиент получит сумму:

FV = PV *(1+ k год ) = 1281,25 руб.

Сложные проценты

В финансовой практике основная часть расчетов ведется с использованием схемы сложных процентов.

Применение схемы сложных процентов целесообразно в тех случаях, когда:

проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

срок ссуды более года.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга.

За первый период начисления

FV₁ = PV +I = PV *r = PV*(1+ r);

ØЗа два периода начисления при условии капитализации ранее наращенной суммы
FV₂ = FV₁ *(1+r)=PV*(1+ r)²

…….

Øза nпериодов начисления формула примет вид:

FV = PV • (1 + r)ⁿ = PV • k_н , ( 1‑20)

где:

ð FV– наращенная сумма долга;

ðPV– первоначальная сумма долга;

ðr – ставка процентов в периоде начисления;

ðn– количество периодов начисления;

ðk_н – коэффициент (множитель) наращения сложных процентов[10].

Эта формула (1-20) называется формулой сложных процентов.

Таким образом, накопление капитала по схеме сложных процентов об­разует возрастающую числовую последовательность PV, FV ₁ ,FV₂ ,… FV_n которая представляет собой геометрическую прогрессию с первым членом –PV .

Геометрический рост по правилу сложных процентов при n > 1 обгоняет арифметическую прогрессию простых процентов. Так, например, трижды заработав на вложенные 10 тыс. руб. проценты (процентные деньги) по 1,5 тыс. руб. в год, вкладчик имеет в конце срока = 10 000 + 3*1 500 = 14,5 тыс. руб., тогда как наращение сложными процентами приносит ему будущую стоимость 15,209 тыс. руб. При удлинении срока вклада эта тенденция усиливается.

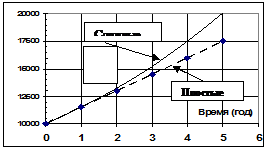
Рис. 1‑4 Рост вложенной суммы при начислении простых и сложных процентов по одинаковой ставке r.

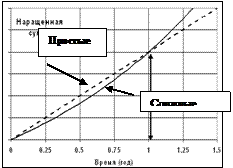
Рис. 1‑5 Фрагмент рисунка 1-4

Как видно из рисунка 1-5, при краткосрочных ссудах (менее одного года) начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.

При любом r,

если 0 < n < 1, то (1 + n*r) > (1 +r)ⁿ;

если n = 1, то (1 +n*r) = (1 + r)ⁿ .

если n > 1, то (1 + n*r) < (1 + r)ⁿ;

Таким образом, для лиц, предоставляющих кредит:

более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);

более выгодной является схема сложных процентов, если срок ссуды превышает один год;

обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

Нетрудно заметить, что величина FVсущественно зависит от значений r и n. Например, будущая величина суммы всего в 1,рубль при годовой ставке 15% через 100 лет составит 1174313,45 рублей!!!

На рис. 1-6 приведен график, отражающий рост суммы в 1,00 при различных ставках сложных процентов.

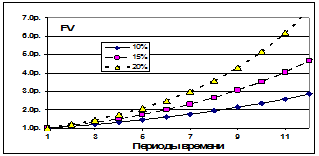
Рис. 1‑6 Рост суммы в 1.00 по ставкам сложных процентов

Примечание

Как мы уже отмечали, различие начисления простых и сложных процентов состоит в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу.

Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучаемого явления с постоянными абсолютными приростами. Сложные проценты характеризуют процесс роста первоначальной суммы со стабильными темпами роста, при наращении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста.

Согласно общей теории статистики, для получения базисного темпа роста необходимо перемножить цепные темпы роста. Поскольку ставка процента за период является цепным темпом прироста, то цепной темп роста равен:

(1 + r).

Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста, имеет вид:

(1 + r)ⁿ .

Базисные темпы роста или коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, могут быть легко табулированы ( Приложение 2)и использованы при проведении финансовых расчетов. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке r.

Пример 1‑12

Сумма в размере 15 000 рублей дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение:

Наращенная сумма

FV = PV* (1 +r)*n =15000 *(1 + 0'1)² =

или

FV = PV * k_н = 15000 * 1,21 = 18150 рублей,

где k_н[11] = 1,21

Сумма начисленных процентов

I = FV - PV = 18150 - 15000 = 3150 рублей

Таким образом, через два года необходимо вернуть общую сумму в размере 18150 рублей, из которой 15000 рублей составляет долг, а 3150 рублей– "цена долга".

Пример 1‑13

Сумма в 10000 помещена в банк на депозит сроком на 4 года. Ставка по депозиту – 10% годовых. Проценты по депозиту начисляются раз в год. Какова будет величина депозита в конце срока?

Решение

По условиям данной операции известными величинами являются:

Первоначальная сумма вклада PV = 10000,

процентная ставка r = 10%,

срок n = 4 года.

FОпределим будущую величину вклада:

ðна конец первого периода:

FV₁ = PV + PV* r = PV*(1 + r) = 10000*(1 + 0,1) = 11000.

ðдля второго периода величина FV будет равна:

FV₂ = FV₁ + FV_1* r = PV*(1 + r) + PV*(1 + r)*r =

PV*(1 + r)²= 10000*(1 + 0,1)² = 12100.

ðДля последнего периода (n = 4):

FV₄ = FV₃ + FV_3×* r = PV*(1 + r)⁴= 10000*(1 + 0,1)⁴ = 14641.

Переменная ставка процентов

Необходимо отметить, что основная формула сложных процентов предполагает постояннуюпроцентную ставку на протяжении всего срока начисления процентов. Однако, предоставляя долгосрочную ссуду, часто используют изменяющиеся во времени, но заранее зафиксированные для каждого периода ставки сложных процентов. В случае использования переменных процентных ставок, формула наращения имеет следующий вид:

FV = PV*(1+ r₁)ⁿ * 1+ r₂)ⁿ *…(1+ r_k)ⁿ =PV* 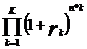( 1‑26)

гдеr_k – последовательные во времени значения процентных ставок;

n_k– длительность периодов, в течение которых используются соответствующие ставки.

Пример 1‑19

Фирма получила кредит в банке на сумму 250000долларов сроком на 5 лет. Процентная ставка по кредиту определена:

для первого года – в 10% для 1-го года,

для 2-го года предусмотрена надбавка к процентной ставке в размере 1,5%,

для последующих лет предусмотрена надбавка к процентной ставке второго года в размере 1%.

Определить сумму долга, подлежащую погашению в конце срока займа

Решение

FV = PV *(1 + r₁)ⁿ¹ * (1 + r₂)ⁿ² * … * (1 + r_k)^nk =

=250000 * (1 + 0,1) * (1 + 0,115) * (1 + 0,125)³ = 436581.3 доллара

Таким образом, сумма, подлежащая погашению в конце срока займа, составит 436581.3 доллара, из которых 250000 долларов являются непосредственно суммой долга, а 186581.3 доллара – проценты по долгу.

Дисконтирование

В практике финансовых расчетов часто приходится решать задачи, обратные определению наращенной суммы: по уже известной наращенной сумме (FV) следует определить неизвестную первоначальную сумму долга (PV).

Наиболее часто такие ситуации возникают при разработке условий финансовой сделки, когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом[12], а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount).

Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.

Различают математическое дисконтирование и коммерческий (банковский) учет.

Банковский учет

Банковский учет заключается в покупке денежных обязательств, (на­пример, векселя[13]) банком по цене, которая меньше номинальной указанной в ней суммы[14]. В этом случае говорят, что вексель учитывается и клиент получает сумму:

PV = FV -D, ( 1‑33)

где FV - номинальная сумма данного обязательства; PV - цена покупки век­селя банком; D - дисконт, сумма процентных денег (доход банка

Схема расчетов по дисконтированию показана на рис.4-8 для случая, когда до срока оплаты векселя векселедателем (т.е. тем, кто его выдал) остался год

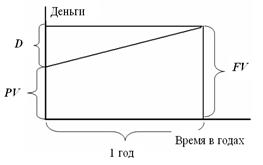
Рис. 1‑8 Схема дисконтирования

Для расчета дисконта могут быть использованы как простая, так и сложная учетные ставки.

FПростая учетная ставка[15]:

D = FV - PV = FV * n * d = FV * t / T * d , ( 1‑34)

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Отсюда:

PV = FV - FV * n * d = FV * (1 - n * d)[16] = FV*кd ( 1‑35)

где k_d = (1 - n * d) – дисконтный множитель.

Очевидно, что чем выше значение учетной ставки, тем больше дисконт.

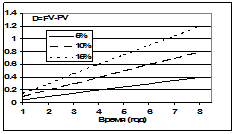
Рис. 1‑9 Зависимость величины дисконта от величины простой учетной ставки

Пример 1‑25

Вексель выдан на 5000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Решение:

Для определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств:

t = 13 (август) + 30 (сентябрь) + 31 (октябрь) + 17 (ноябрь) - 1 = 90 дней.

Отсюда, определяемая сумма:

PV = FV * (1 - t / T *d) = 5000 (1 - 90 / 360 * 0,08) = 4900 руб.

Тогда дисконт составит:

D = FV - PV = 5000 - 4900 = 100 руб.

или

D = FV *( t/T * d )= 5000 * 90 / 360 * 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4900 руб., а банк при наступлении срока векселя получит дисконт в размере 100 руб.

FСложная учетная ставка:

PV = FV *(1 - d)ⁿ ( 1‑36)

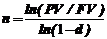(1‑37)

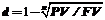( 1‑38)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к величине, уменьшаемой на величину дисконта.

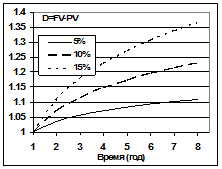
Рис. 1‑10 Зависимость дисконта от величины сложной учетной ставки.

Пример 1‑26

Вексель на сумму 100 тыс. руб. и сроком платежа через 3 года продан с дисконтом по сложной учетной ставке 30% годовых.

Какова сумма дисконта и современная величина платежа?

Решение

PV = FV*(1-d)ⁿ =100000*(1-0.3)³ = 34300 руб.

D =FV-PV = 100000 – 34300 = 65700 руб.

Пример 1‑27

Заемщик должен возвратить кредитору долг в сумме 1 млн. 200 тыс. руб. Первоначальная сумма была выдана заемщику ссудой в размере 1 млн. руб. под 50% годовых, начисляемых по сложной учетной ставке. На какой срок заемщику выдавалась ссуда, если T=360 дней?

Решение.

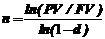= ln(1/1.2)/ln(1-0.5) = 0.263 года @ 94 дня.

Чистый приведенный доход

При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени.

Центральным показателем в рассматриваемом методе является показатель NPV (net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков. Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.

При разовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением:

( 4‑1)

где CF_k – годовые денежные поступления в течение n лет, k= 1, 2, …,n;

Z – стартовые инвестиции;

r – ставка дисконтирования.

Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет (m), то формула для расчета модифицируется:

( 4‑2)

Показатель NPV характеризует абсолютный прирост[40], поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты:

при NPV> 0 проект может быть принят;

при NPV< 0 проект не принимается,

при NPV= 0 проект не имеет ни прибыли, ни убытков

Пример 4‑1

Найти чистый дисконтированный доход проекта, требующего стартовых инвестиций в объеме 150 тыс. руб., денежный поток которого задан рис4-1, по ставке дисконтирования 10% годовых.

Рис. 4‑1 Денежный поток инвестиционного проекта

Решение

На листе Excel создадим таблицу, подобную приведенной на Рис.4-2.

Рис. 4‑2 рагмент рабочего листа MS Excel c вычислением величины чистого дисконтированного потока в соответствии с формулой (4-1)

Рис. 4‑3 Фрагмент рабочего листа MS Excel в режиме отображения формул c вычислением величины чистого дисконтированного потока в соответствии с формулой (6-1)

В ячейках столбца :

"А" размещены периоды поступления (оттока) денежных средств;

"В" размещаются величины денежных потоков в соответствующие периоды;

"С" размещены аккумулированные значения денежных потоков в данном периоде. Например, в ячейке "С4" может быть записано: =C3+B4;

"D" размещаются формулы расчета величины коэффициента дисконтирования денежных потоков. Например, в ячейке "D3" записывается: =(B3/(1+0)^A3)/B3; в ячейке "D4" записывается: =((B4/(1+0.1)^A4))/B4 и т.д.;

"E" значения дисконтированных денежных потоков. Например, в ячейке "E4" записывается: =B4*D4

"F" записываются формулы расчеты аккумулированных дисконтированных денежных потоков в соответствующий период времени. Например, в ячейке "F3" записывается величина денежного потока в начальный период (начальные инвестиции): =D3; в ячейке "F4" записывается: =F3+E4 и т.д.

“G”записывается логическая функция анализа окупаемости проекта. Например, в ячейке “G3”записывается формула:=ЕСЛИ(C3>0;"Проект окупается";"Проект не окупается"),которая копируется в ячейки G4:G11 таблицы.

Таким образом, в результате выполненных вычислений получаем:

Чистый дисконтированный доход = 32,01

Дисконтированный доход = -(-150)+32,01 = 182,01

Готовый результат 182,01 в одной клетке дает табличная формула =NPV(10%;C4:C11), вызывающая специальную финансовую функцию со ссылкой на норму дисконтирования _("Ставка")и табличные координаты блока значений ("Значения1".,..)элементов денежного потока, расположенных в хронологическом порядке.

В русских версиях MS Excel функция NPV имеет название ЧПСили в НПЗ в младших версиях.

Рис. 4‑4 Диалоговое окно функции ЧПС()

Необходимо заметить, что, несмотря на название, функция NPV (ЧПС, НПЗ)вычисляет не весь чистый, а только дисконтированный доход, то есть Present Value (PV) денежного потока (на один период назад от первого поступления/выплаты).

Пояснения.

Функция ЧПС() (НПЗ)возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис функции: ЧПС(ставка;значение1;значение2; ...)

Ставка — ставка дисконтирования за один период.

Значение1, значение2, ... — от 1 до 29 аргументов, представляющих расходы и доходы.

Значение1, значение2, ... должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

Значение1, значение2, ... могут вводится либо в отдельные окна либо списком ( при этом, порядок ввода значений (либо значений в списке) определяется порядком поступлений и платежей)

Для вычисления чистого дисконтированного дохода к выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных затрат нулевого периода, записанное в таблице в ячейке В3

=ЧПС(10%;B4:B11)+B3

?Метод определения чистой текущей стоимости часто используется при оценке эффективности инвестиций. Он позволяет определить нижнюю границу прибыльности и использовать ее в качестве критерия при выборе наиболее эффективного проекта.

Положительное значение NPV является показателем того, что проект приносит чистую прибыль, после покрытия всех связанных с ним расходов

Пример 4‑2

Сравним два проекта, денежные потоки которых представлены на рис.4-5 , при значениях ставки дисконтирования 15%

Рис. 4‑5 Исходные данные и решение примера 4-2

Пример 4‑3 Диалоговое окно функции ЧПС() для Проекта 1

В ячейке “B8”Разместим формулу ЧПС(), которую скопируем в ячейку “С8”

В ячейках “В9” и “С9” вычисляется значения чистого дисконтированного дохода для Проектов 1 и 2.

Выполненные расчеты показывают целесообразность принятия Проекта 2, не смотря на то, что величины денежных потоков обоих проектов различаются несущественно.

Срок окупаемости

Для анализа эффективности инвестиций часто используется такой показатель, как срок окупаемости (payback period method) – продолжительность времени, в течение которого дисконтированные на момент завершения инвестиций прогнозируемые денежные поступления равны сумме инвестиций. Иными словами – это количество лет, необходимых для компенсации стартовых инвестиций[41]:

( 4‑3)

Наиболее просто период окупаемости может быть определен как:

( 4‑4)

Пример 4‑4

Рассчитать срок окупаемости проекта, для которого размер инвестиций составляет 1 млн. руб., а денежные поступления в течение 5 лет будут составлять: 250; 400; 800; 900; 900 тыс. руб. соответственно. Ставка дисконтирования 15%.

Решение.

На листе Excel создадим таблицу, подобную приведенной на рис.4-7

Рис. 4‑6 Фрагмент рабочего листа Excel с исходными данными и решением примера 4-3

Рис. 4‑7 Фрагмент рабочего листа Excel в режиме отображения формул с исходными данными и решением примера 6-3

В ячейках:

C1:G1 размещены номера периодов поступления денежных средств;

C2:G2размещены величины поступления денежных средств (величины CF_k);

C3:G3размещены формулы дисконтирования поступающих денежных средств. Например, в ячейке С3записана формула =C2/((1+15%)^C1),соответствующая левой части формулы 6-3;

C4:G4записаны формулы вычисления накопленного в данный период дисконтированного денежного потока. Например, в ячейке С4 записана формула =B4+C3 (суммавеличины инвестиции и поступивших в этот период (1) денежных средств), а в ячейке D4записывается формула =C4+D3 (суммавеличины накопленного дисконтированного потока и поступивших в этот период (2) денежных средств) и т.д.

Анализируя построенную таблицу легко видеть, что инвестиции полностью окупаются в интервале между 2 и 3 периодами. Тогда в соответствии с 7-4 период окупаемости может быть найден как:

=D1+(-D4/E3) =2+480,15/526,01 =2,91 года

Таким образом, период, реально необходимый для возмещения инвестированной сумы, составит 2,91 года или 2 года и 332 дня.

Период окупаемости может быть также определен, если в ячейку С5записать формулу: =ЕСЛИ(C4>0;C1-(B4+C3)/C3;0)[42]и скопировать ее в остальные ячейки строки.

Индекс рентабельности

Индекс рентабельности (benefit-cost ratio, profitability index - PI) пока­зывает, сколько единиц современной величины денежного потока приходит­ся на единицу предполагаемых первоначальных затрат. Для расчета показа­теля используется следующая формула:

( 4‑5)

Если величина критерия PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивая тем са­мым наличие положительной величины NPV.При этом норма рентабельно­сти превышает заданную и проект следует принять.

При PI = 1 величина NPV= 0 и инвестиции не приносят дохода.

В слу­чае, если PI < 1, проект не обеспечивает заданного уровня рентабельности и его следует отклонить

Применение показателя PIчасто бывает полезным в случае, когда су­ществует возможность финансирования нескольких проектов, но при этом инвестиционный бюджет фирмы ограничен.

Пример 4‑5

Фирма рассматривает возможность участия в финанс