Три метода начисления простой процентной ставки.
Тема 1. ПРОЦЕНТНЫЕ СТАВКИ.
1.Принцип неравноценности денег во времени. Дать определение понятиям: проценты, наращенная сумма ссуды, процентная ставка наращения. Понятие финансовой операции. Доходность финансовой операции.Рубль, заработанный сегодня, стоит дороже рубля, заработанного завтра без учета инфляции. Процент-абсолютная величина дохода от предоставления денег в долг в любой его форме.I-процент, S- наращенная сумма, P-первоначальная сумма. i=I*100% /P(процентная ставка-явл. измерителем степени доходности любой финн.операции, тогда процентная ставка наз. доходностью.
2.Простая процентная ставка наращения. Вычисление процентов, наращенной суммы. Множитель наращения.Простая процентная ставка-ставка, при кот. база начисления всегда остается постоянной. I=Pni S=P(1+ni) n=t/K (где n-срок, t-число месяцев, K-временная база=360)
Три метода начисления простой процентной ставки.
Метод точных %- К=365
Метод обыкновенных %- К=360
Метод обыкновенных % с приблизительным числом дней(30)- К=360
4.Сложная процентная ставка наращения. Вычисление наращенной суммы. Множитель наращения.Сложная %ставка-ставка наращения, при которой база начисления явл переменной. 1год S1=P(1+i) 2год S2=P(1+i)(1+i) 3год S3=P(1+i)(1+i)(1+i) из этого следует S=P(1+i)n Сложные %ставка применяется для долгосрочных ссуд сроком более 1 года.
5.Номинальная процентная ставка наращения. Вычисление наращенной суммы при начислении процентов m раз за год.Номинальная %ставка наращения- ставка не за период,а за год(j). m-кол-во начислений процентов за год i=j/m S=P(1+j/m)mn
6.Определение эффективной ставки. Расчёт эффективной ставки.Эффективная ставка - годовая ставка сложных %,кот дает тот же процент, что и m разовом начислении. Эффективная ставка измеряет реальный относительный доход, кот получает в целом за год от начисления процентов. P(1+i)n = P(1+j/m)mn i=(1+j/m)n-1(эффективная ставка наращения). Замена в договоре номинал ставки j при m-разовом начислении на эффективную ставку i не изменит финансовых обязательств сторон,т.е. обе ставки эквивалентны в финансовом отношении. S(1-d)n=S(1-f/m)mn
d=1-(1-f/m)m
Непрерывное начисление процентов. Сила роста. Вычисление наращенной суммы при непрерывном начислении процентов. Связь дискретных ставок наращения с силой роста.
Непрерывное начисление %- начисление % , при количестве начислений mà∞. S=lim[P(1+j/m)mn]=Peᵟn, где ᵟ - сила роста-%ставка при непрерывном начислении процента.
ᵟ=ln(1+i)=mln(1+j/m) S=P(1+j/m)mnà j=m(eᵟ/m -1) ᵟ=m*ln(1+j/m)
8.Математическое дисконтирование. Вычисление современной стоимости при использовании простых, сложных, номинальных процентов и силы роста. Дисконтные множители (коэффициенты дисконтирования). Понятие дисконта.Дисконтирование- обратный процесс наращения, закл в определении первоначальной суммы по известной наращенной сумме, сроку финансовой операции и процентной ставке. Сколько нам сейчас необходимо инвестировать (положить в банк),чтобы через n лет получить заданную сумму при заданной %ставке.P=S/(1+i)n; Pt=St/(1+r)t
r-ставка дисконтирования-min-ая норма доходности, приемлемая для инвестора.Опр-ся из стоимости альтернативных вложений.
Тема 2. УЧЁТНЫЕ СТАВКИ.
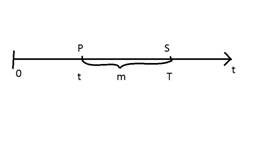
9.Понятие операции банковского (коммерческого) учета. Простая учётная ставка. Расчёт стоимости векселя при его досрочном учёте. Наращение по простой учётной ставке.Суть операции:банк или иное финн учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене,кот меньше суммы,указан на векселе.Владелец векселя имеет возможность получить деньги раньше указанного срока, хотя и не в полном объеме. При учете векселя применяется банковский или коммерческий учет. Сформулируем задачу банковского дисконтирования. По данным рисунка по заданной сумме S,кот будет выпущена через m, требуется определить сумму займа P при известной учетной ставке d.%за использование ссудой выплачиваются заранее в момент предоставления долга или дисконта.D=S-P В этом случае применяются и простые и сложные учетные ставки.
10.Банковский учёт по сложной учётной ставке. Расчёт стоимости векселя при его досрочном учёте. Наращение по сложной учётной ставке.Банковское дисконтирование по сложной учетной ставке осуществляется P=S(1-d)n àS=P/(1+d)n Дисконтирование по сложн учетн ставке выгоднее для должника чем по простой.
11.Номинальная и эффективная учётная ставка. Банковское дисконтирование и наращение по номинальной и эффективной учётной ставке.f-номинальная годовая учетная ставка. Эффективная ставка - годовая ставка сложных %,кот дает тот же процент, что и m разовом начислении. Эффективная ставка измеряет реальный относительный доход, кот получает в целом за год от начисления процентов. P(1+i)n = P(1+j/m)mn i=(1+j/m)n-1(эффективная ставка наращения). Замена в договоре номинал ставки j при m-разовом начислении на эффективную ставку i не изменит финансовых обязательств сторон,т.е. обе ставки эквивалентны в финансовом отношении. S(1-d)n=S(1-f/m)mn
d=1-(1-f/m)m
Номинальная %ставка наращения- ставка не за период,а за год(j). m-кол-во начислений процентов за год i=j/m S=P(1+j/m)mn
Непрерывное дисконтирование по сложной учетной ставке-дисконтирование на бесконечно малых отрезках времени. 1/mà0 (mà∞) Т.к.при непрерывном начислении % начало и конец периода начисления %совпадают,то номинальные %ставки j и f перестают различаться.Польз-ся одной %ставкой-силой роста ᵟ. P=S*e-ᵟn S=P*eᵟn
Тема 3. ПОТОКИ ПЛАТЕЖЕЙ.
Критерий внутренняя норма доходности проекта. Экономический смысл. График зависимости чистого приведённого дохода от ставки дисконтирования для типичного проекта. Недостатки критерия внутренняя норма доходности проекта.
IRR Внутренняя норма доходности –сттавка дисконтирования r при кот чист привед доход проекта=0. NPV=∑ FCFt/(1+r)=0 à r = IRR
IRR это такое значение ставки дисконтирования при кот дисконт ден поток от операц деят-ти = дисконтир ден потоку от инвестиц деят-ти.
IRR<r проект эфф-ый и NPV>0
IRR<r проект неэфф-ый и NPV< =0
IRR хар-т устойчивость проекта к изменению ставки дисконтирования.Чем больше разница между IRR и ставкой дисконтирования тем больше запас устойчивости проекта.Такой анализ предост менеджеру сопоставить доходность проекта и риск. Если весь проект осущ-ся за счет заемных ср-в, то IRR равна наибольш % ставке, под кот можно взять кредит чтобы расплатиться из доходов от реализации проекта. Недостатки IRR: 1проект может иметь несколько значений IRR или не иметь вообще
2при сравнении 2 и более взаимозаключающих проектов кот различ по сроку жизни и масштабам инвестиций применение критерия может привести к ошибке
3 в случае если ставка дисконтир меняется во времени то простого способа оценки IRR не сущ-ет
4 IRR не обладает св-м аддитивности
5показатель IRR м б рассчитан только численными методами с применением программ обеспечения или с помощью приближенных оценок.
22.Критерий индекс доходности (рентабельности).Экономический смысл. Недостаток критерия индекс доходности.PI – отношение дисконтир ден потока от операц деят-ти к дисконтиров ден потоку от инвестиц деят-ти. PI=∑CFt/(1+r)t / ∑INVt/(1+r)t
PI>1 то NPV>0
PI< = 1 то NPV< =0
PI-относит показатель хар-й уровень дохода на единицу инвестиц затрат. Недостаток в том что он не обладает свойством аддитивности.
23.Критерий дисконтированный срок окупаемости проекта. Экономический смысл. Графическое изображение дисконтированного срока окупаемости проекта.DPP –время за кот дисконтир ден поток от операц деят-ти становится равен дисконтир ден потоку от инвестиц деят-ти.
∑CFt/(1+r)t = ∑INVt/(1+r)t
1Не учитывает доходы за пределами срока окупаемости.2не учитывает разницу во времени получения доходов в пределах срока окупаемости. 3не обладает св-м аддитивности.
Тема 5. Оценка финансовых активов (инструментов).
Тема 1. ПРОЦЕНТНЫЕ СТАВКИ.
1.Принцип неравноценности денег во времени. Дать определение понятиям: проценты, наращенная сумма ссуды, процентная ставка наращения. Понятие финансовой операции. Доходность финансовой операции.Рубль, заработанный сегодня, стоит дороже рубля, заработанного завтра без учета инфляции. Процент-абсолютная величина дохода от предоставления денег в долг в любой его форме.I-процент, S- наращенная сумма, P-первоначальная сумма. i=I*100% /P(процентная ставка-явл. измерителем степени доходности любой финн.операции, тогда процентная ставка наз. доходностью.
2.Простая процентная ставка наращения. Вычисление процентов, наращенной суммы. Множитель наращения.Простая процентная ставка-ставка, при кот. база начисления всегда остается постоянной. I=Pni S=P(1+ni) n=t/K (где n-срок, t-число месяцев, K-временная база=360)
Три метода начисления простой процентной ставки.
Метод точных %- К=365
Метод обыкновенных %- К=360
Метод обыкновенных % с приблизительным числом дней(30)- К=360
4.Сложная процентная ставка наращения. Вычисление наращенной суммы. Множитель наращения.Сложная %ставка-ставка наращения, при которой база начисления явл переменной. 1год S1=P(1+i) 2год S2=P(1+i)(1+i) 3год S3=P(1+i)(1+i)(1+i) из этого следует S=P(1+i)n Сложные %ставка применяется для долгосрочных ссуд сроком более 1 года.
5.Номинальная процентная ставка наращения. Вычисление наращенной суммы при начислении процентов m раз за год.Номинальная %ставка наращения- ставка не за период,а за год(j). m-кол-во начислений процентов за год i=j/m S=P(1+j/m)mn
6.Определение эффективной ставки. Расчёт эффективной ставки.Эффективная ставка - годовая ставка сложных %,кот дает тот же процент, что и m разовом начислении. Эффективная ставка измеряет реальный относительный доход, кот получает в целом за год от начисления процентов. P(1+i)n = P(1+j/m)mn i=(1+j/m)n-1(эффективная ставка наращения). Замена в договоре номинал ставки j при m-разовом начислении на эффективную ставку i не изменит финансовых обязательств сторон,т.е. обе ставки эквивалентны в финансовом отношении. S(1-d)n=S(1-f/m)mn
d=1-(1-f/m)m
